【第5回】四分位数-後編

2021年12月30日 15:57

こんにちは。kenstyです。
前回に引き続き四分位数についてまとめていきたいと思います。
文部科学省の検定教科書の定義および表計算ソフトのQUARTILE.INC関数・QUARTILE.EXC関数で採用している定義を比較してまとめた記事です。

前回の復習

前回は奇数個（9個）の数から成るデータについて四分位数を考えました。結果を再度まとめておきます。

偶数個の数から成るデータ

今回は偶数個（8個）の数から成るデータ
　23　24　25　26　29　30　34　39
の四分位数を考えてみたいと思います。まずは、結論です。

今回は第1四分位数・第3四分位数とも、表計算ソフトのどちらの関数の採用している定義に基づいたものと異なります。それでは順に見てみましょう。

QUARTILE.INC関数

前回と同じように、数字の間に旗を立てながら、何％の位置にあるかを確認してみたいと思います。

旗の数は全部で7本です。2つ例を見てみましょう。
25より左にある旗は2本ですので、25は 2/7 = 約28.6% の位置です。
30より左にある旗は5本ですので、30は 5/7 = 約71.4% の位置です。
このように、データ全体の何%の位置にあるかが決まります。
今回はちょうど25%、50%、75%の位置にある数がありませんので、その前後から補間を行います。

まず、第2四分位数から見てみましょう。
26 は 3/7 = 12/28 の位置で、29 は 4/7 = 16/28 の位置です。
50％は 14/28 ですので、これらのちょうど中央にあります。従いまして、26と29の平均をとった27.5が第2四分位数になります。

次に、第1四分位数です。
24 は 1/7 = 4/28 の位置で、25 は 2/7 = 8/28 の位置です。
また、25%は 7/28 であることに注意して下の図を見てください。

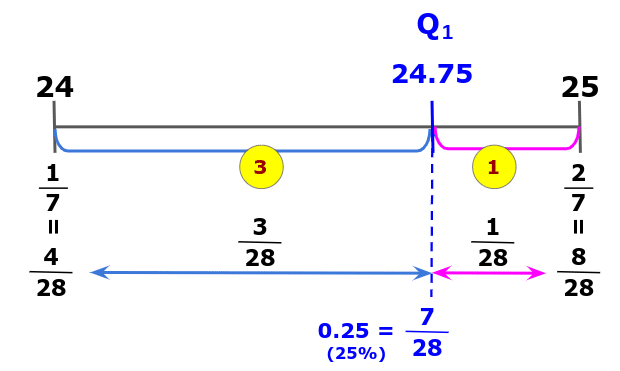
上の図より、第1四分位数（データ全体の25%の位置の数）は、数直線上の2点、A(24)とB(25)を結んだ線分ABを3:1に内分する点の座標と定めるのが自然です。このように補間を行うことで、24.75であると分かります。

第3四分位数についても同様です。

上の図より、第3四分位数（データ全体の75%の位置の数）は、数直線上の2点、A(30)とB(34)を結んだ線分ABを1:3に内分する点の座標と定めるのが自然です。このように補間を行うことで、31であると分かります。

以上が、QUARTILE.INC関数の定義に基づいた四分位数です。

QUARTILE.EXC関数

上とほとんど同様です。旗を数字の間に加え、両端にも立てるところがポイントでした。

旗の数は全部で9本です。2つ例を見てみましょう。
25より左にある旗は3本ですので、25は 3/9 = 約33.3% の位置です。
30より左にある旗は6本ですので、30は 6/9 = 約66.7% の位置です。
このように、データ全体の何%の位置にあるかが決まります。
今回もちょうど25%、50%、75%の位置にある数がありませんので、その前後から補間を行います。
先程と同じように補間を行うことで、第1四分位数は24.25、第2四分位数は27.5、第3四分位数は33であることが分かります。

以上が、表計算ソフトの関数が採用している四分位数の定義でした。
ちょうど25%の位置に当たる数がない場合などの前後の数からの補間が少々ややこしいと思われます。数学Ⅱで内分点の公式を学習したあとに積極的にそれを利用してみてもよいかもしれません。

Pythonの場合

PythonのNumpyモジュールやPandasモジュールで採用されている四分位数の定義も表計算ソフトのQUARTILE.INC関数と同じ定義が採用しています。

Numpy

ソースコード

import numpy as np
data9 = np.array([23,24,25,26,26,29,30,34,39])
print(np.quantile(data9,0.25))
print(np.quantile(data9,0.5))
print(np.quantile(data9,0.75))

実行結果

25.0
26.0
30.0

Pandas

ソースコード

import pandas as pd
data9 = np.array([23,24,25,26,26,29,30,34,39])
df9 = pd.DataFrame(data9)
df9.describe()

実行結果

検定教科書定義の四分位数をPythonで

それではここで、検定教科書で採用されている定義に基づいた四分位数をPythonのプログラムを利用して求めてみましょう。

四分位数を求めるデータをリスト list に代入し、その長さを n とします。
四分位数を n を用いて表してみましょう。

nが4で割り切れる数のとき

k = n/4 とおくと、
第1四分位数： ( list[k-1] + list[k] ) / 2
第2四分位数： ( list[2*k-1] + list[2*k] ) / 2
第3四分位数： ( list[3*k-1] + list[3*k] ) / 2
と表せることが分かります。

nが4で割って1余る数のとき

k = (n-1)/4 とおくと、
第1四分位数： ( list[k-1] + list[k] ) / 2
第2四分位数： list[2*k]
第3四分位数： ( list[3*k] + list[3*k+1] ) / 2
と表せることが分かります。

nが4で割って2余る数のとき

k = (n-2)/4 とおくと、
第1四分位数： list[k]
第2四分位数： ( list[2*k] + list[2*k+1] ) / 2
第3四分位数： list[3*k+1]
と表せることが分かります。

nが4で割って3余る数のとき

k = (n-3)/4 とおくと、
第1四分位数： list[k]
第2四分位数： list[2*k+1]
第3四分位数： list[3*k+2]
と表せることが分かります。

Pythonでのコーディング

ここまで場合分けしたものをまとめます。
四分位数を求めるデータをリスト list に代入し、n = len(list) としました。
n ≡ 0 (mod 4) のとき、 k = n/4
n ≡ 1 (mod 4) のとき、 k = (n-1)/4
n ≡ 2 (mod 4) のとき、 k = (n-2)/4
n ≡ 3 (mod 4) のとき、 k = (n-3)/4
とおきました。このことから、kはnを4で割った数の小数点以下を切り捨てた数と言えます。
つまり、 k = int(n/4) とすれば、すべての場合をまとめられそうです。
もっと工夫すればさらにコードを短くできそうですが、とりあえずは下記で実行できます。（listの定義後のコードです。）

n = len(list)
k = int(n/4)
if n % 4 == 0:
    q1 = (list[k-1] + list[k])/2
    q2 = (list[2*k-1] + list[2*k])/2
    q3 = (list[3*k-1] + list[3*k])/2
elif n % 4 == 1:
    q1 = (list[k-1] + list[k])/2
    q2 = list[2*k]
    q3 = (list[3*k] + list[3*k+1])/2
elif n % 4 == 2:
    q1 = list[k]
    q2 = (list[2*k] + list[2*k+1])/2
    q3 = list[3*k+1]
else:
    q1 = list[k]
    q2 = list[2*k+1]
    q3 = list[3*k+2]
print(f"第1四分位数: {q1},  第2四分位数: {q2},  第3四分位数: {q3}")

実際に、12個、13個、14個、15個の数から成るデータで確認してみましょう。

list = [1,2,3,4,5,6,7,8,9,10,11,12]

第1四分位数: 3.5,　第2四分位数: 6.5,　第3四分位数: 9.5

list = [1,2,3,4,5,6,7,8,9,10,11,12,13]

第1四分位数: 3.5,　第2四分位数: 7, 　第3四分位数: 10.5

list = [1,2,3,4,5,6,7,8,9,10,11,12,13,14]

第1四分位数: 4,　第2四分位数: 7.5,　第3四分位数: 11

list = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]

第1四分位数: 4, 　第2四分位数: 8, 　第3四分位数: 12

情報の授業でどのように扱うか

四分位数の定義はここまで見てきました表計算ソフトの関数が採用している定義の他にも複数の定義があります。その中で、最も分かりやすいと思われるものを文部科学省の検定教科書で採用されているに過ぎません。
それではこの違いを踏まえ、情報の授業の中でどう指導していくのがよいかですが、私は次のように考えています。

表計算ソフトではQUARTILE.INC関数を用いる。
四分位数には複数の定義があり、数学の時間に学習したものと、ここで学習したものは異なるため、値が若干異なっていることを伝える。
四分位数はデータのおおよその散らばり方を把握するための指標であるため、ある程度データが大きいときはこの定義の違いによる若干の違いはそれほど問題にならないことも伝える。
~~定義の細かい違いを知りたい人は、kenstyのnoteの記事を読むことを薦める。~~（自重）

つまり「数学の時間に習ったものとちょっと違うけど、四分位数はあくまで散らばりを見るための目安なのであまり気にしない」というおおらかな立場です。

実際の運用上はそうであっても、表計算ソフトなどで四分位数の定義としてどのようなものが採用されているのかはおさえておきたいものです。私自身、一度、四分位数の定義は整理しておきたいと思いまして今回記事にしてみました。

検定教科書で採用されている定義で四分位数を求めるPythonプログラムの改良方法についてご助言をいただける方がいらっしゃいましたら、コメントしていただけると本当に嬉しいです。
2021年の更新はこれで一区切りにします。みなさまが、良いお年をお迎えくださいますことをお祈り申し上げます。ありがとうございました！