図式で学ぶ線形代数 番外編その2 ~ベクトル解析~
連載の記事一覧:
#1 図式の基礎と線形代数の基礎
#2 スペクトル分解と特異値分解
#3 テンソル積およびトレース・転置・内積
#4 行列が作るヒルベルト空間
番外編 列ベクトルや行列での微分
番外編その2 ベクトル解析
3次元実ベクトル空間 $${ \R^3 }$$ でのベクトル解析を図式で表現する方法を述べます。多少の慣れが必要ですが,図式を活用すると,数式を用いる場合と比べて素直に表現できて,またいろいろな公式をすぐに導けるようになります。この記事により,図式のおもしろさが少しでも伝われば幸いです。
概要
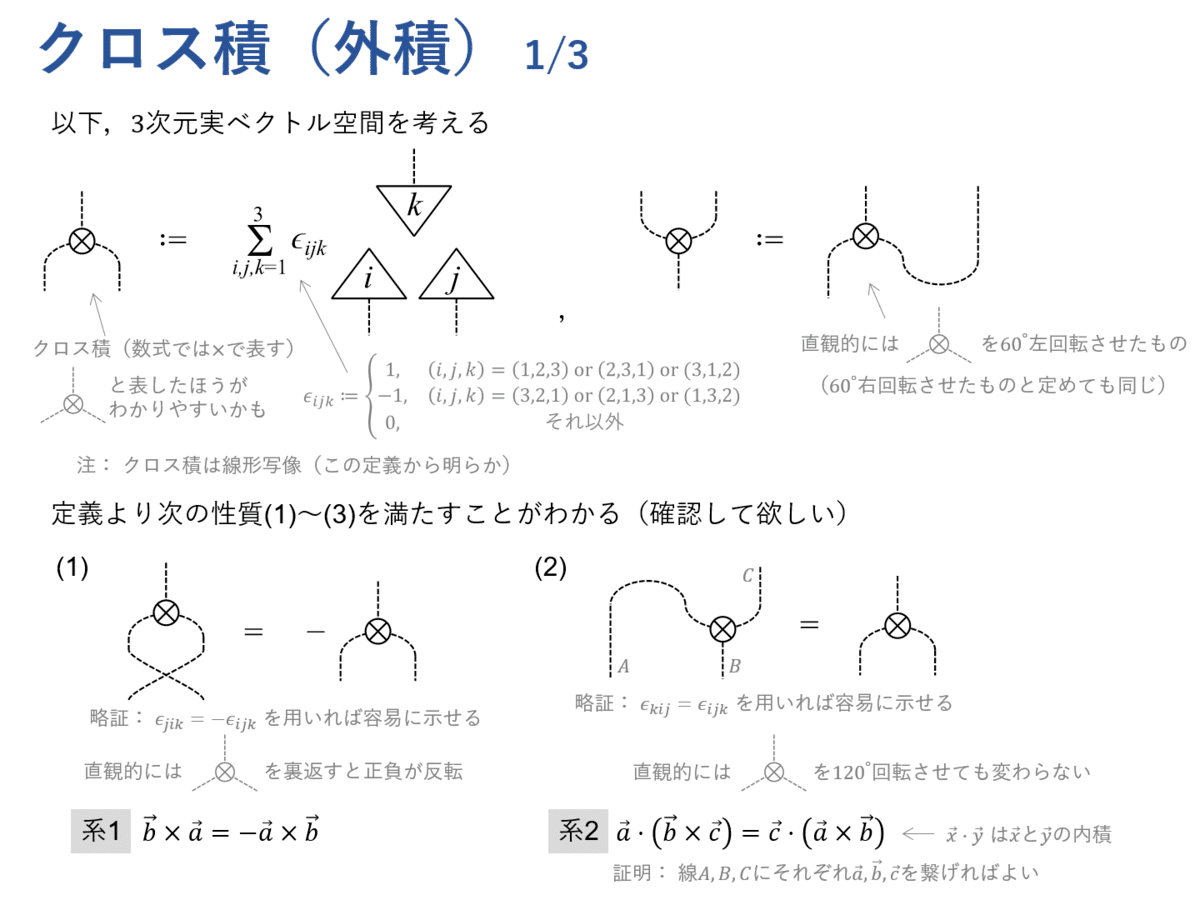
次の行列を導入します。

ただし,$${ \epsilon_{ijk} }$$ は
$$
\epsilon_{ijk} \coloneqq
\begin{dcases}
1, & (i,j,k) \in \{ (1,2,3), (2,3,1), (3,1,2) \} \\
-1, & (i,j,k) \in \{ (1,3,2), (2,1,3), (3,2,1) \} \\
0, & それ以外 \\
\end{dcases}
$$
で定義され,レヴィ・チヴィタの記号とよばれます。2個のベクトル $${ \vec{a} }$$ と $${ \vec{b} }$$ のクロス積(外積やベクトル積ともよばれます) $${ \vec{a} \times \vec{b} }$$ は,次の図式で表されます。

次式が成り立つことが知られています。
$$
(\vec{a} \times \vec{b}) \times \vec{c} = (\vec{a} \cdot \vec{c}) \vec{b} - (\vec{b} \cdot \vec{c}) \vec{a} \qquad (1)
$$
ただし,$${ \cdot }$$ は内積です。細かな規則はひとまずスキップして先に結論を示すと,図式では次のようにして導出できます。

この右辺第1項にある $${ \vec{a} }$$ と $${ \vec{c} }$$ が線でつながったものは内積 $${ \vec{a} \cdot \vec{c} }$$ のことです。このため,この項は $${ (\vec{a} \cdot \vec{c}) \vec{b} }$$ を表しています。右辺第2項も同様です。このことから,この図式が式(1)と対応することが何となくわかるのではないかと思います。
図式での計算方法を学べば,上のような図式を描くだけで導出できるようになります。数式を用いて式(1)を導出する場合と比べて,図式による導出のほうが素直でかつ速いと思います。
詳細
PDF資料
詳細は下記のPDF資料にまとめましたので,よろしければご覧ください。
なお,この資料には,記事「図式で学ぶ線形代数 番外編 ~列ベクトルや行列での微分~」の内容も含まれています。
スライド
上記のPDF資料の内容を抜粋したスライドも掲載しておきます。大まかな内容を知りたい方は,こちらをご覧ください。






この連載は,書籍「図式と操作的確率論による量子論」の内容の一部を紹介したものです(この記事のほうが詳しく述べている箇所もあります)。
