
図式で学ぶ量子論 #3 ~確率論としての古典論・量子論(前編)~
連載の記事一覧:
#1 量子論の数学的構造
#2 CP写像の基礎
#3 確率論としての古典論・量子論(前編)
#4 確率論としての古典論・量子論(後編)
#5 プロセスの表現
番外編 2準位系から多準位系への演繹による拡張は難しい
番外編その2 堀田先生の書籍(中略)演繹的に導けていない
番外編その3 量子もつれ状態と非局所相関について
番外編その4 堀田先生からの『最終回答』へのコメント
前々回では古典論と量子論の数学的構造について説明し,前回ではCP写像(つまり量子論におけるプロセス)について説明しました。今回と次回では,この構造に対して確率の概念を導入しながら,古典論と量子論の確率的な性質を説明します。
量子論の確率的な性質を統一的な形で記述するためにはCP写像は不可欠です。CP写像の詳しい知識がなくても概要は何となくわかると思いますが,わからない表現などがあれば前回の内容を復習してください。
放棄エフェクトと確率
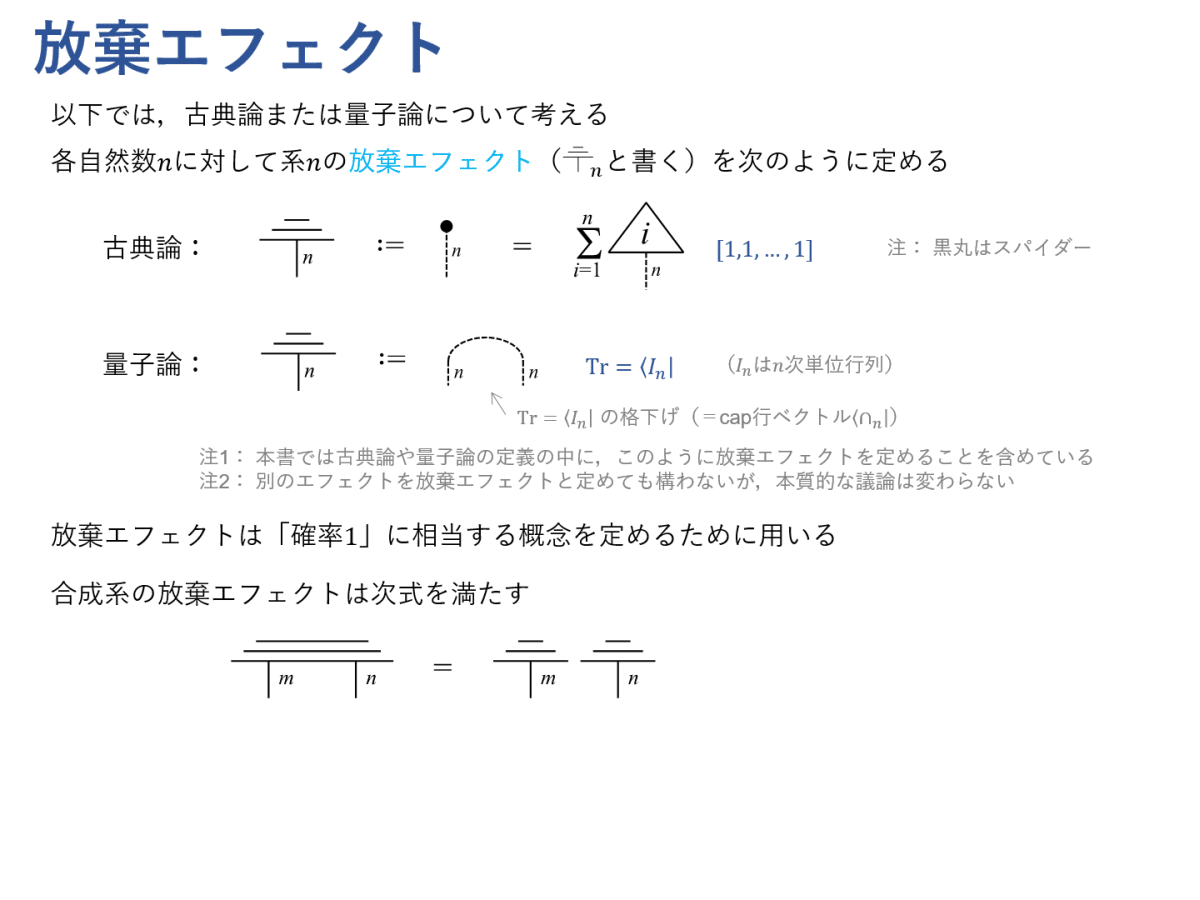
まず,放棄エフェクトという概念を導入します。これは,「確率 $${ 1 }$$」に相当する概念です。

「状態を準備する確率」や「状態を準備してプロセスを施す結合確率」をスカラー(=非負の実数)に対応付けます。正規状態とは,量子論では密度行列(=トレースが $${ 1 }$$ である半正定値行列)のことです。
正規状態に対して放棄エフェクトを施すと常に $${ 1 }$$ を返しますので,状態に含まれている(正規であるということ以外の)情報が失われることになります。この意味で,直観的には放棄エフェクトとは「系の状態を捨てる」ことを表します。
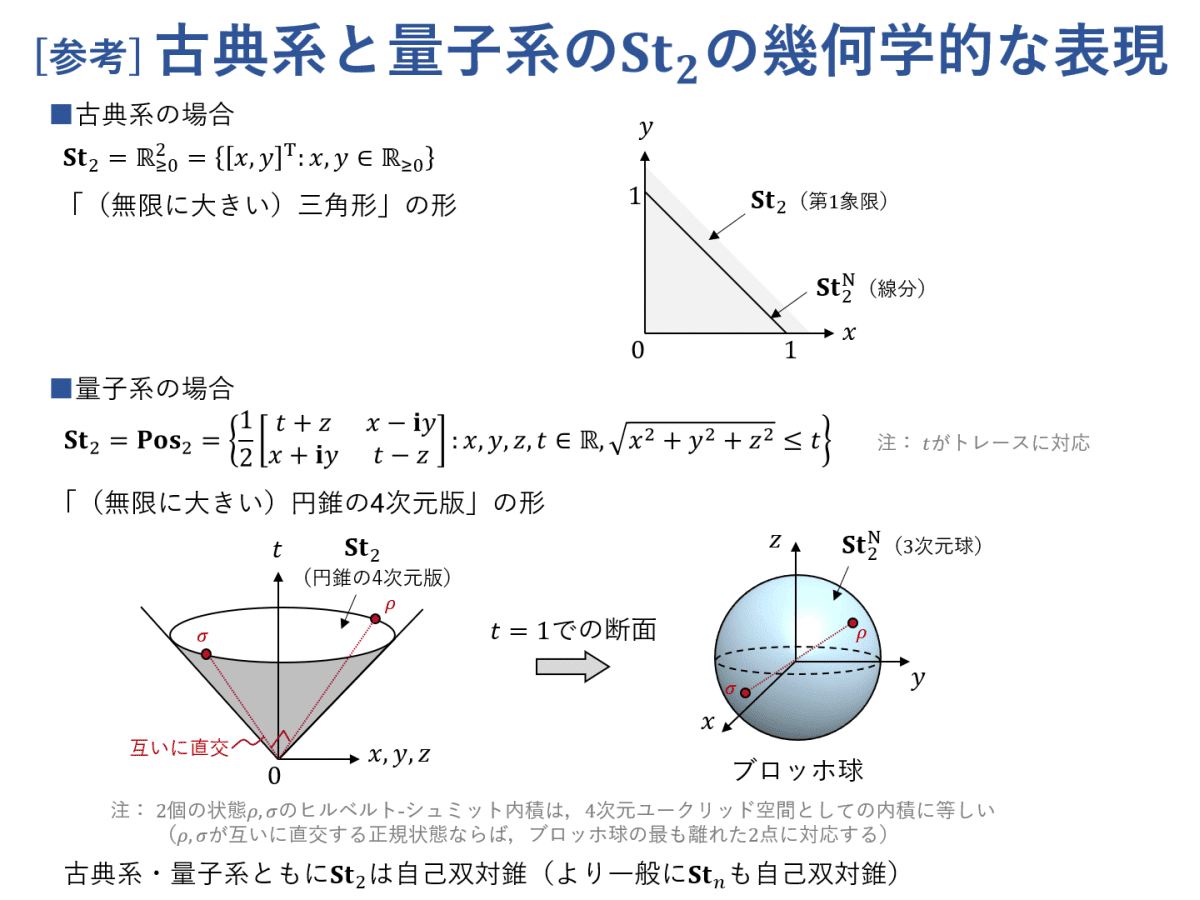
古典系と量子系の状態空間の幾何学的な表現です。状態空間はどちらも自己双対錐になっています。なお,自己双対錐については「図式で学ぶ線形代数 #4」をご参照ください。
すべての正規状態はある超平面(具体的には放棄エフェクトを施すと $${ 1 }$$ になるような要素をすべて集めた超平面)の上にあります。この超平面は,量子論の場合にはトレース $${ 1 }$$ の $${ 2 }$$ 次エルミート行列をすべて集めた集合です。

古典系と量子系の状態は,状態空間が張る実ヒルベルト空間(複素ヒルベルト空間ではありません)の要素として考えると直観的にわかりやすいことが多いです。和とスカラー倍は,確率の和と結合確率に対応しています。
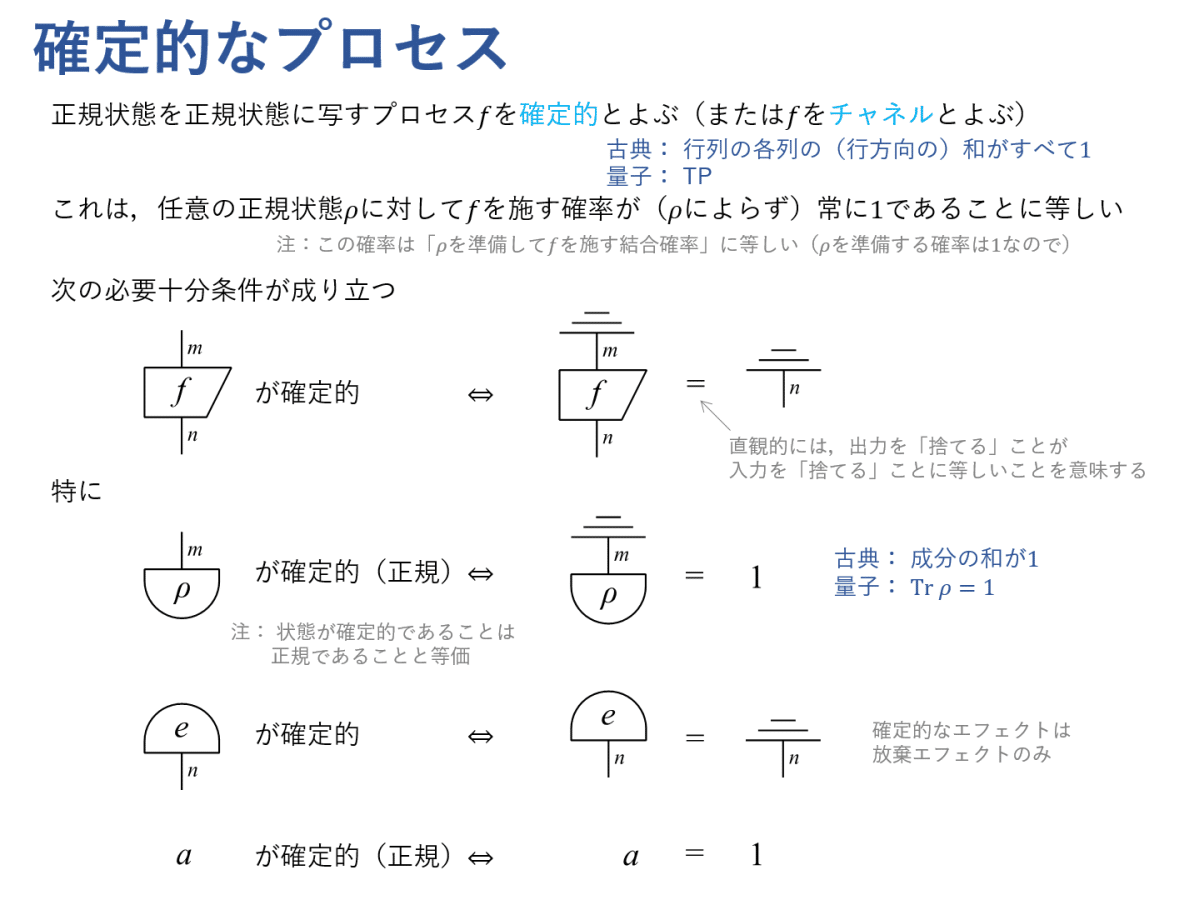
確実に施せるプロセスとして,「確定的」という概念を導入します。量子論では,確定的なプロセスはしばしば量子操作や量子チャネル(通信路)のようによばれます。「確率1」に相当する概念である放棄エフェクトを用いて必要十分条件を表せます。
テストと測定

テストと測定を導入します。これらは,「いずれか1個を確実に施せるようなプロセスの組」として解釈できます。直観的には,テストは理想測定のような「状態を出力する測定」を表し,測定は一般の光子検出器のような「状態を出力しない測定」を表します。なお,任意の確定的なプロセス $${ f }$$ に対して,$${ f }$$ のみから成る集合(つまり $${ \{ f \} }$$)はテストです。
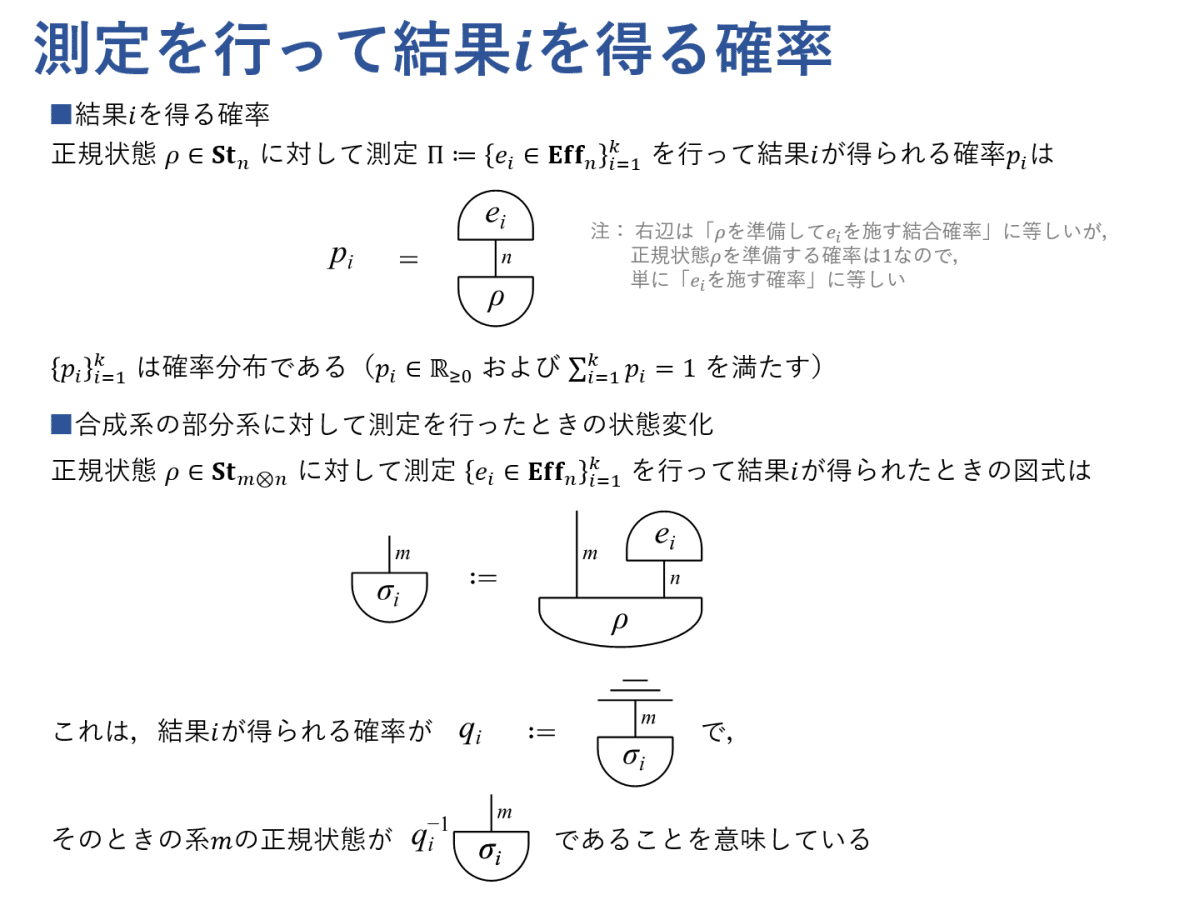
正規状態に対してある測定を行って特定の測定結果が得られる確率や,合成系の状態の部分系に対して測定を行ったときの状態変化などを,素直な形で表せます。

古典論と量子論において,エフェクトの組が測定であるための必要十分条件を示します。量子論では,測定とはPOVM(Positive Operator-Valued Measure)で表せるもののことです。測定とPOVMは一対一に対応しています。
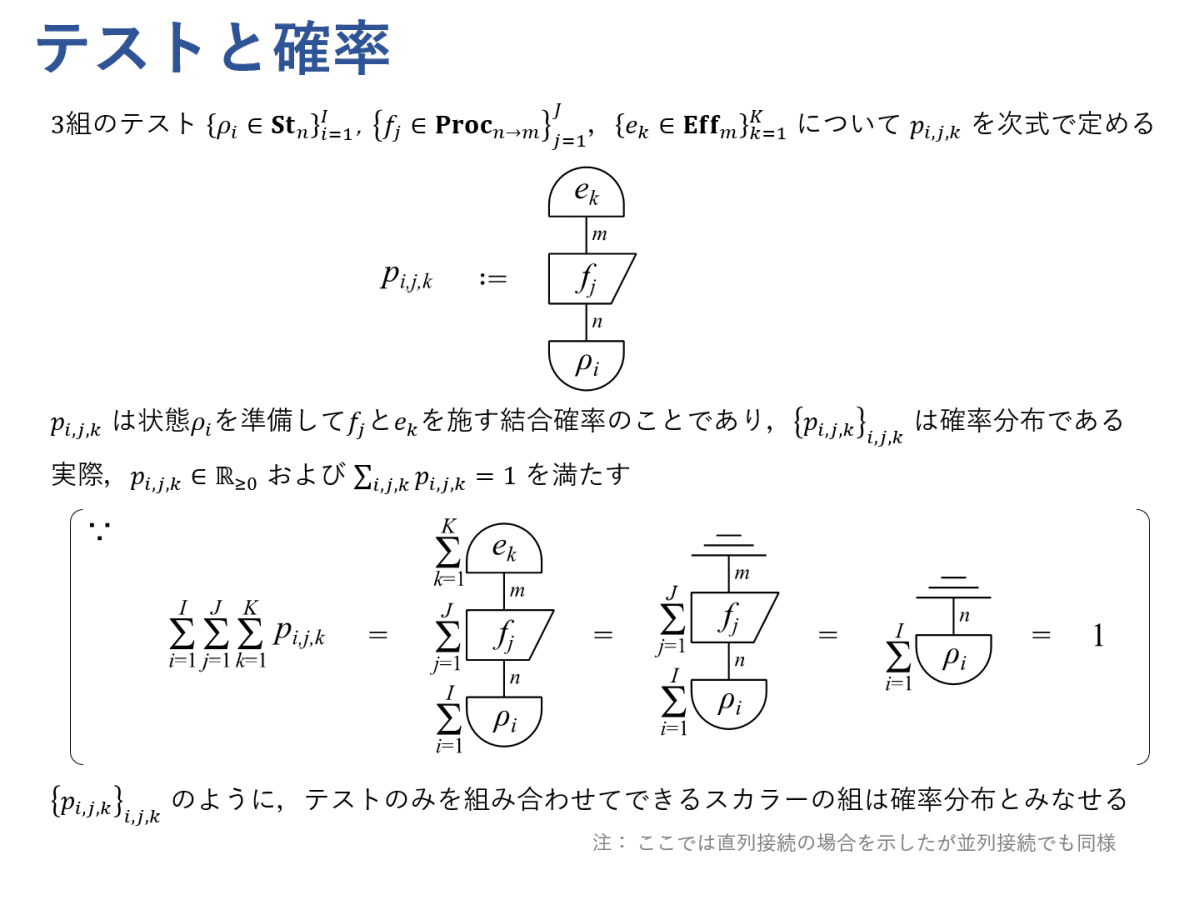
テストのみを直列・並列に接続してできるスカラーの組は確率分布とみなせます。

任意のテスト $${ \{ f_i \}_{i=1}^k }$$ について,そのテストに入力する正規状態が決まれば「各 $${ f_i }$$ が施される確率」が定まります。
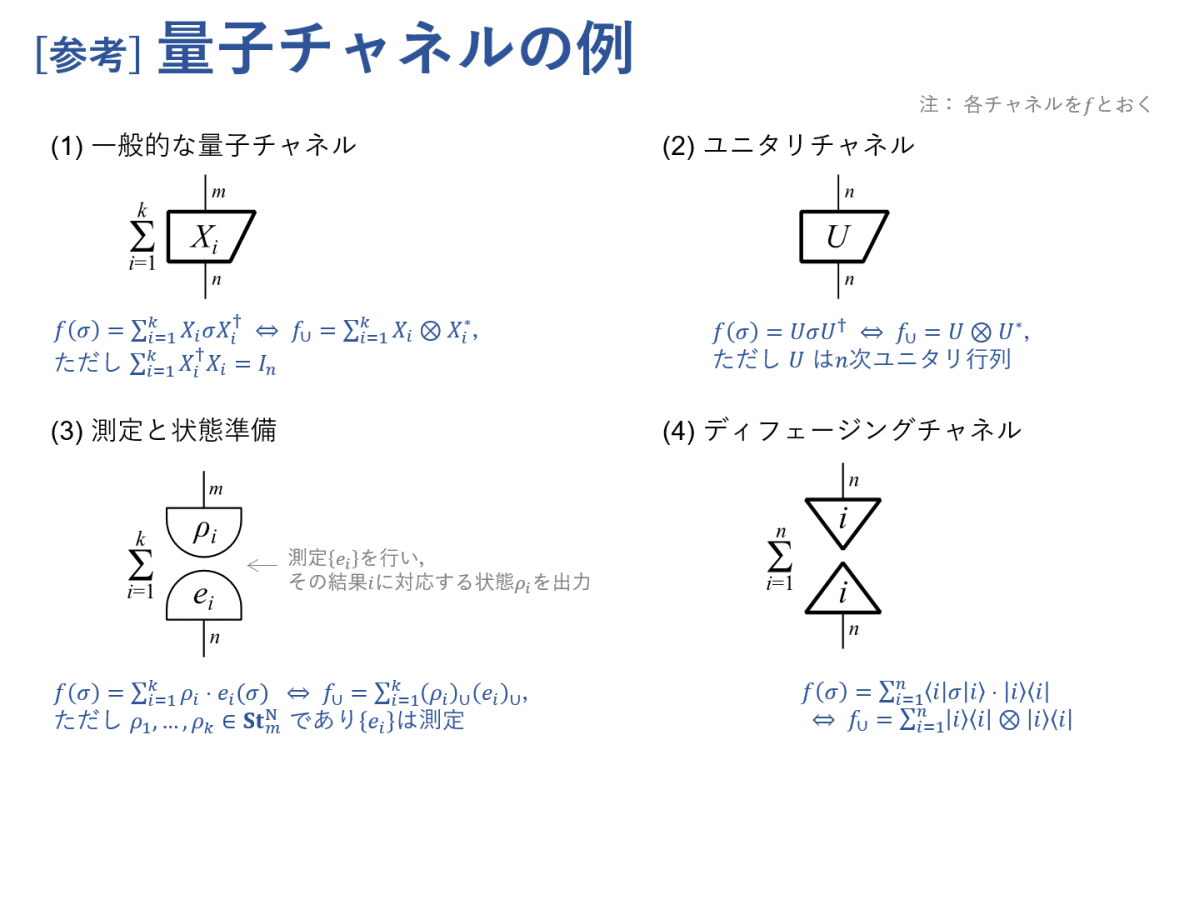

(1) 一般的な量子チャネルと(クラウス表現しています),その具体例として,(2) ユニタリチャネル,(3) 測定と状態準備,(4) ディフェージングチャネル,(5) 制御ユニタリチャネルを示します。
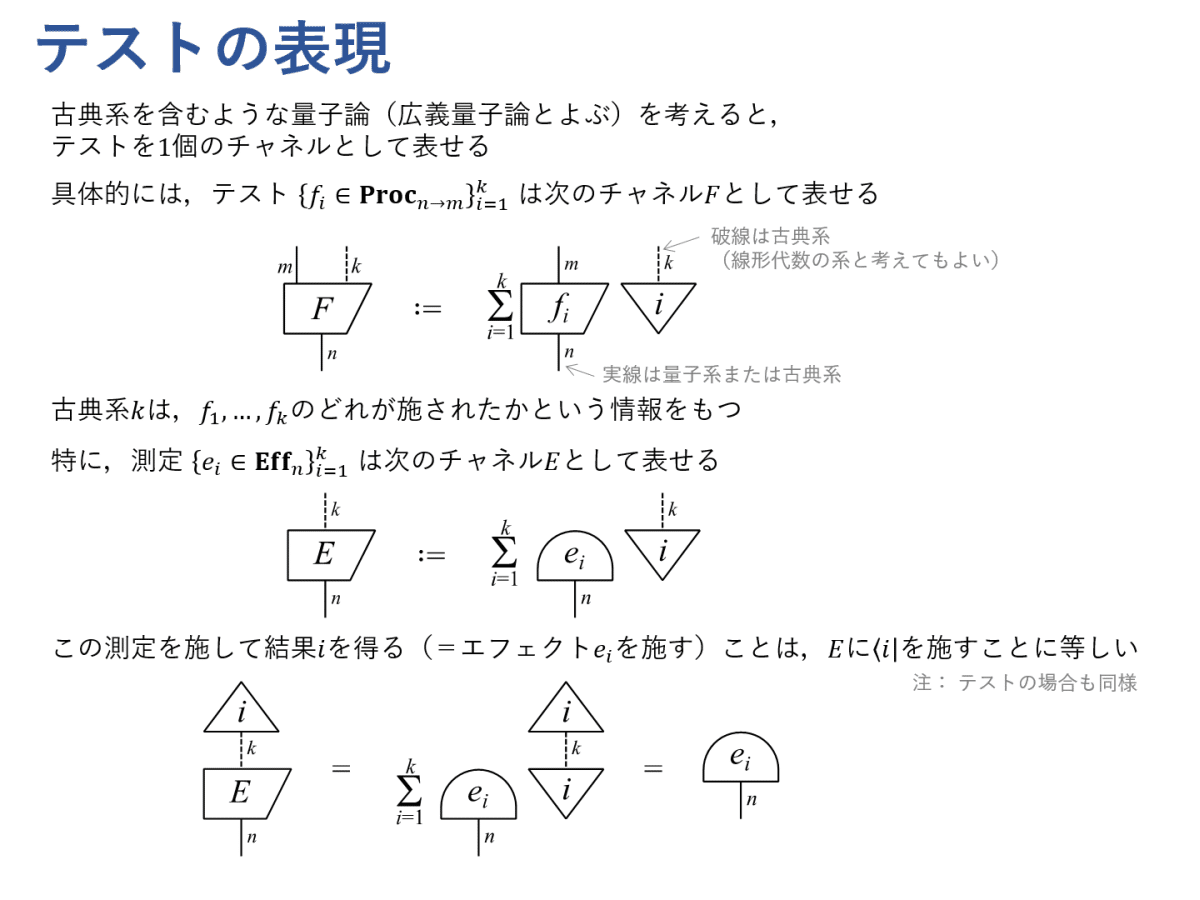
古典系を用いれば,テストをプロセスの組ではなく $${ 1 }$$ 個のチャネルとして表せます。測定も同様に $${ 1 }$$ 個のチャネルとして表せます。

理想測定の図式です。理想測定はテスト(つまり「状態を出力するような測定」)の一種です。
次回では,引き続き確率的な性質について述べる予定です。
この記事は,書籍「図式と操作的確率論による量子論」の内容の一部を紹介したものです(この記事のほうが詳しく述べている箇所もあります)。
この記事が気に入ったらサポートをしてみませんか?
