
条件文「AならばB」は命題ではない? ~ 論理学における条件法の真理値設定の問題点
条件文「AならばB」は命題ではない? ~ 論理学における条件法の真理値設定の問題点
以前書いていたレポートを書き直しました。PDFファイルです。
条件文「AならばB」は命題ではない? ~ 論理学における条件法の真理値設定の問題点
http://miya.aki.gs/miya/miya_report32.pdf
『数学にとって証明とはなにか』(瀬山士郎著、講談社)を読んで、もともとあった条件文への違和感がさらに強まってしまったので、本稿でその問題点をまとめてみました。前件が偽ならば後件が真であれ偽であれ全体として真になるという、条件法の論理学的真理値設定が普遍性を持つという根拠をどこにも見いだせない、そしてその論理学的真理値設定が本当にトートロジーと呼べるのか疑わしい論理を生み出していることを指摘しています。論理学の専門家の方々からのご意見もいただければ幸いです。
<目次>
1.条件文は命題ではない? (1ページ)
2.対偶にしてみると条件文の真理値への違和感が際立つ(4ページ)
3.矛盾から任意の命題が無条件に導出されるのか? (5ページ)
4.A→(B→A)とはいったい何なのか? (7ページ)
5.条件法における論理学的真理値設定の普遍性を正当化する根拠は見当たらない:ダメットの条件法真理値に関する見解について (8ページ)
6.ナンセンス文は真とは言えない (11ページ)
7.論理は現実との関連を失えばその真偽の根拠を失う (13ページ)
8.トートロジーは現実から見いだされるもの (14ページ)
<引用・参考文献> (16ページ)
以下、6章と8章の内容を本記事に掲載しておきます。
6.ナンセンス文は真とは言えない
ネット上において、条件法の論理学的真理値設定に関して次のような説明を見つけた。
命題「X>5ならばX>3である」は真
・「Xがどんな数であっても」なりたつ
↓
・X=7を入れて、「7>5ならば7>3である」も真
・X=4を入れて、「4>5ならば4>3である」も真
・X=1を入れて、「1>5ならば1>3である」も真
ということで以下の論理学的真理値設定が成立するというのである。
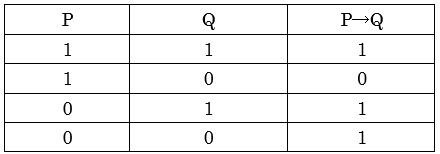
(大森武「論理式の真偽を定義する」https://note.com/omori55/n/n75730aa4806f より)
しかし説明に無理があるのではなかろうか。「4>5ならば4>3である」「1>5ならば1>3である」というナンセンス文が果たして「真」と言えるのだろうか?
そして上記真理表の二行目が欠けている。なぜならX>5と前件で条件付けされている時点で後件が偽になりえないからである。
そもそも「X>5ならばX>3である」という命題はXがどんな数でも成り立つのではなく、X>5といった時点でXは5より大きな数であると前提されているはずである。命題そのものが正しいことは、命題における変数Xがどんな値でも良いこととは違うのである。
これらのことから「X>5ならばX>3である」を前提条件とした真理値は正確には次のようになるであろう。

ここまで見てきたように、条件法の真理値は前提条件ごとに様々な値(あるいは値がない)を取りうるのであって、論理学的真理値設定が普遍的であるという根拠がどこにも見当たらないのである。
8.トートロジーは現実から見いだされるもの
野矢氏はウィトゲンシュタイン『論理哲学論考』を引用し、トートロジーについて説明を試みている。
4.462 トートロジーと矛盾は現実の像ではない.それはいかなる可能な状態も描出しない.前者は可能な状態のいずれをも許容し,後者はひとつとして許容しないからである.
6.1 論理の命題はトートロジーである.
6.11 それゆえ論理の命題は何ごとも語らない.
6.1222 このことは,なぜ論理の命題が経験によって確証も反証もされえないのかという問に光を投げかける.
野矢氏は、トートロジー(例えば前件肯定式)が常に現実世界と合致していることとを、「情報量ゼロ」「それゆえ論理の命題は何ごとも語らない」(野矢、39ページ)としているが果たしてそうであろうか?
そうではない。トートロジーが現実世界と常に一致していること(つまりいずれをも許容)、まさにそれこそがトートロジーである根拠なのである。論理が現実世界から離れて「何ごとかを語る」ようではトートロジーとは言えないのである。
つまりトートロジーとは現実世界、私たちの知覚として現れる具体的経験(そこから現実世界認識が構築される)が究極的な根拠となっているのである。
一方「矛盾」とは、「直線4本からなる三角形」「丸い四角(丸っこい四角ではない)」「平面において交わる平行線」というように、私たちの具体的経験として現れることがない、絵に描こうにも描けない、想像しようにも想像さえできない、そういう状態のことを言うのであって、トートロジーと同列に扱うことなどできないのである。上記ウィトゲンシュタインの言葉を借りれば「ひとつとして許容しない」となるであろうか。
結局のところ、論理が正しいかどうかを確かめる術は、究極的には具体的事例と照らし合わせる以外にないのである。出発点となる公理系がある。それが「正しい」ものなのか、と聞かれれば、それぞれ具体的事例を挙げて「実際にそうなっているだろう」と納得させるしか究極的には方法がないのである(このあたりヒュームの抽象観念論がもっと見直される必要があると私は感じている)。
私たちの日常経験、日常的現実世界認識から導かれたよりシンプルな公理系、そこから演繹(つまり推論)することでより複雑な論理を構成していく。正しい公理系から推論したのだからおそらく正しい論理であろうという信頼のもと、論理学やら数学の体系が構築されているのである。
一方、論理学的に正しいと言われていても、それに日本語を当てはめてみるとナンセンス文になってしまう場合、果たしてその論理は「正しい」あるいはトートロジーであると言えるのであろうか?
A∧(¬A)→P
カピバラが草食であり、かつ草食でなければ、カピバラは空を飛べる
A→(B→A)
カピバラは草食である→地球に生物が存在しなければ、カピバラは草食である
<引用文献>
野矢茂樹著『論理学』(東京大学出版会、1994年)
