
note連続講義 第1章‐2 極限と微分の関係 第1章‐3 導関数と高階導関数
~はじめに~
皆さんこんにちは,lim_sub_r_boyです.ここ最近の小話を軽くした後で本編に入ろうと思います.最近は中学3年生の受験生の勉強を教えていて中々note連続講義を書くことができていなかったのですが,教えていくたびに成長する姿を見ると『教育』の世界はやはり楽しいなと感じます.という感じで,この連続講義は1週遅れていてこのままいくと予定と合わなさそうなので,先週はこれを言って終わってしまったのですが今週は次回の話も今回の学習に似ているので,まとめて一本にしたいと思います.
ということでまずは先週の復習…
・極限というものを知った.
・三角関数,指数関数が入った極限公式を知った.
・問題演習を通し,極限を学んだ.
それでは,さっそく本編に入っていきましょう.
~微分とは~
まずは第1章‐2の方からスタートということで,ここでのキーワードは『微分』です.その言葉の意味から考えたいと思います.微分とは,ある関数における傾きを求めることを言います.言葉を図にして表しましょう.
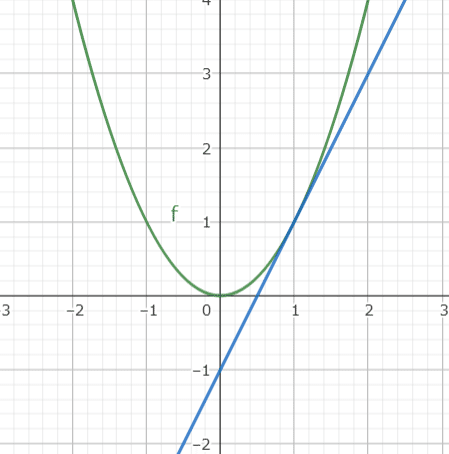
この図は$${y=x^2}$$という関数の座標$${(1\,,\,1)}$$の点に対して,$${y=2x-1}$$という1つの接線(1次関数)を引いた図です.この1次関数こそが微分の鍵となるのです.先ほどの言葉に$${+\alpha}$$するならば,ある点における接線を求めることこそが微分なのです.正確に言うと切片は微分だけじゃ求まらないのですが,傾きに関しては微分を使って求めることができます.この傾きを求めることを『微分係数を求める』といいます.それでは,この微分係数の定義式を今から見ていきたいと思います.
$${\mathrm{def.}\text{微分係数}\\f'(a)=\lim\limits_{h\to a}\dfrac{f(h)-f(a) }{h-a}}$$
今回からは定義式は$${\mathrm{def.}}$$とし,定理は,$${\mathrm{the.}}$$とする.それぞれ,definitionとtheoremからきている.
一般の教科書には微分係数の前に,平均変化率があると思うがこの式は微分係数の極限をしないものなので,今回は省かせていただきます.それでは微分係数の定義式にもあるように,微分と極限の関係についてみていこうと思います.
~微分と極限の関係性~
この2つの関係性は簡単に言ってしまえば,平均変化率というものをより厳密化するために極限が平均変化率を助けるという関係性だ.これが合体することで微分公式を作ることができる.
図の様にすごくこの2つは仲がいいわけです.あまりこんなことを言ってしまっては何なのですが,このような図を出すということは,ネタが切れているということです.ということで,次の講の方が重要ではあるので次に進みたいと思います.
~微分の定義~
さっきまでの面白い(?)のは後にして,続いてやるのは第1章‐3である導関数についてです.言葉としては微分と導関数で違いますが意味の違いはありませんのでどちらを使っても問題ありません.さっそくこれは定義を見ないと何も始まらないので定義からやりたいと思います.
$${\mathrm{def.}\\f'(x)=\lim\limits_{h\to0}\dfrac{f(x+h)-f(x)}{h}}$$
ということで,これが定義式です.では問題を解いていきましょうと言われてもさっぱりだと思うので,例題を見ていきましょう.
《例題》次の関数を微分せよ.
$${f'(x)=x^2}$$
$${\mathrm{solv.}}$$
$${f'(x)=\lim\limits_{h\to0}\dfrac{(x+h)^2-x^2}{h}\\f'(x)=\lim\limits_{h\to0}\dfrac{x^2+2hx+h^2-x^2}{h}\\f'(x)=\lim\limits_{h\to0}\dfrac{h(2x+h)}{h}\\f'(x)=\lim\limits_{h\to0}(2x+h)=2x_{//}}$$
このような感じで微分をしていきます.
~微分公式~
続いては微分の公式を紹介していきたいと思います.
~三角関数~
$${(\sin x)'=\cos x\\(\cos x)'=-\sin x\\(\tan x)'=\dfrac{1}{\cos^2x}}$$
~指数・対数関数~
$${(\log x)'=\dfrac{1}{x}\\(\log f(x))'=\dfrac{f'(x)}{f(x)}\\(e^x)'=e^x}$$
~$${n}$$次関数~
$${(x^n)'=nx^{n-1}}$$
これらの公式は全て微分の定義式から導出することができます.$${n}$$次関数に関しては先ほどの例題で示したような感じであります.また,三角関数に関しては和積の公式であったり前回の極限公式を使用するので導出は少し大変でしょう.
~高階導関数~
続いては,1階微分ができるのであれば,2階以上できる関数はもちろんあります.例えば,三角関数は4階目で元の関数に戻るし,指数関数$${e^x}$$は1階目から全く同じ関数です.なので,そのような関数を紹介していきたいと思います.
$${n}$$次関数はまず$${n=0}$$になるので最終的には0となります.なので何階でも微分することは可能ではありません.続いて,三角関数です.この関数は全て何階でも微分可能です.このような$${n}$$階微分可能な関数を,$${C^n}$$級の関数とも言います.
おすすめの演習問題かなと思います.他にも多くの問題があるので,ぜひいろんな問題を解きましょう.
~さいごに~
今回も読んでくださりありがとうございました.ここでは基礎中の基礎である微分しかやっていないので,もっともっと基礎となる部分があります.次週は,応用の部分もやりますがその前に微分の方法についても話そうと思います.
それではまた次回のnote連続講義でお会いしましょう.
さようなら!
