
【写真/動画つき】よく分かるA*アルゴリズム
この記事では、
地図のルート検索やロボットなどで使用されるA*パスファインディングというアルゴリズムについて紹介します。
このアルゴリズムは与えられたマップから最適で最短距離を探すためのアルゴリズムになります。
Googleマップや自動運転ロボットなどの技術の根幹となる経路探索の手法としてのアルゴリズムです。
自己紹介
みなさんこんにちは!
世界を体験できるメディアをミラーワールドを通じて作っているかっつーです。それを作るための背景や思いなどについてはこちらの記事を参考にしてください!
作るまでの具体的なステップについてはこちらの記事をご参考にしてください。
僕は世界のあらゆる境界線に関心があります。細胞や自己と他者、障害、国境、社会的対立など世界は境界線の積分でできていると考えています。
これらの境界線をテクノロジーによって、なめらかにし、自由自在にすることができれば、人々が生きやすいなめらかな社会が実現できると考えています。
この記事の読者ターゲット
ゲームAIの根幹技術であるA*パスファインディングについて簡単に理解したい人
A*パスファインディングの概念的な理解とコード的な理解を紐づけたい人
A*パスファインディングを図解で理解したい人
ゲームAIとA*パスファインディングの関係性や使用場面について理解したい人
この記事を読むのにかかる時間は「5分」です。
A*パスファインディングとは?
あるマップの最短経路を見つけるための効率的な探索手法です。
このアルゴリズムは、ゲームAI、ロボット工学、地理情報システム(GIS)などの様々な分野で応答されている根幹のアルゴリズムです。
A*探索アルゴリズムとも呼ばれます。
A*アルゴリズムは与えられたマップ内のスタート地点から、マップ内のゴールまでの最短ルートを探索します。
このアルゴリズムは1968年にPeter E. Hart、Nils J. Nilsson、Bertram Raphael これら三人が発表した論文で使われた用語がもととなってA*という特殊な名前になりました。
具体的には、スタートからゴールまでの最短経路を確実に見つけるアルゴリズムを許容的(Admissible)と読んだことからその冒頭部分のアルファベットを取って、Aとなりました。
スター(*)の意味は、経済学でもよく用いられる最適な状態を*を使って表しています。
もっともマップ内のスタートからゴールまでの探索回数が最適になるものをA*と表現したのです。
A*パスファインディングの基本的な考え方
A*パスファインディングについて理解するためには3つの重要な要素があります。それは、
スタート
ゴール
コスト
予想コスト
です。
スタート地点とゴール地点はわかるかと思います。
コストは、スタート地点とゴール地点の間の時間や距離、お金などになります。
**スタート地点からの距離や時間、お金などがもっとも少なくなるように移動するにはどうすればよいか?**というのを数学的に解くのがこのA*パスファインディングになります。
具体的には、コストは**コスト関数 f(n)**を用いて探索を行います。
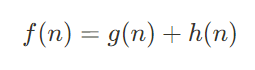
g(n)はスタート地点からn地点までの最小コストです。
h(n)はn地点からゴール地点までの予想コストのことです。
もし仮に、g(n)とh(n)の最適な距離である、g*(n)とh*(n)を神様視点で最初から知っていたら、f*(n)も一撃でも止まりますよね?道に迷うこともないはずです。
しかし、実際にはそんなふうに最初から最適な距離を知ることはできません。
そこで、重要なのが予想コストになります。
予想コストとは?
予想コストは、実装ではヒューリスティック距離h(n)と呼ばれます。これは、正確な距離を表しているのではなく、仮に見積もり予測を立てた距離になります。現在地からゴールまでどれくらいかわからないけど、大体あっちの方!みたいなことは人でもあると思います。
下記で示す実装では、n地点とゴール地点の間を直線距離で結んだユークリッド距離を計算しています。
いわゆる三平方の定理です。


黄色い点からGまでがヒューリスティック距離(予想コスト)になります。
予想コストが最小化する場所を頑張って探していくのがこのA*あるごりすむになります。
その過程をまずは動画で表示します。
具体的な数字を交えながら最適化していく様子を画像とともに下記に示します。
とあるパターン










別の事例


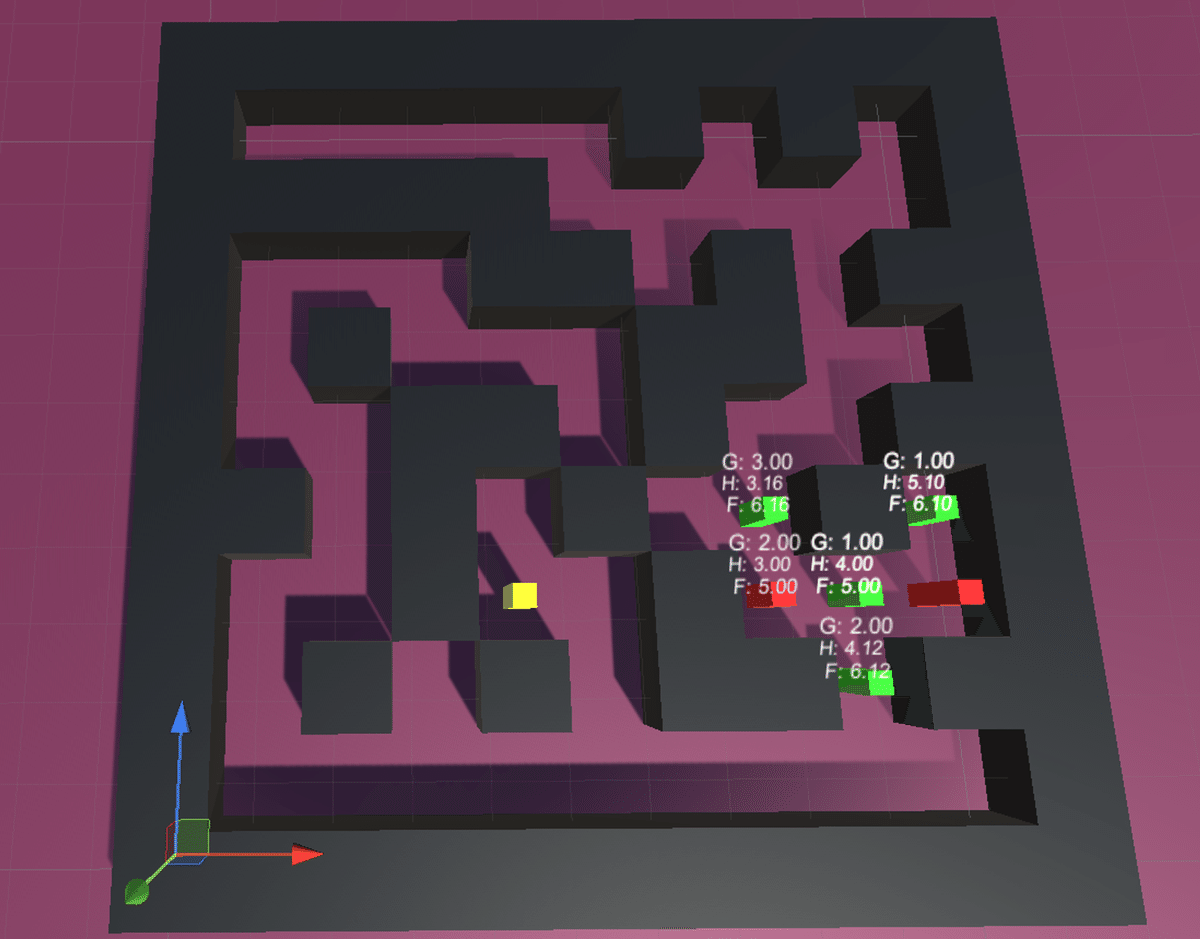










このように、現在位置から移動可能な候補を絞って移動しながら、ゴール地点とn地点との間をユークリッド距離で計算しつつ、もっとも短くなりそうな経路を更に絞っていきながら進んでいることがわかるかと思います。
そうすることで、すべてのマスを計算することなく最短距離を計算することができるのです。
A*アルゴリズムの弱点
一見かなり良さげなアルゴリズムに見えますが、弱点も存在しています。
それは、ゴール地点が移動する場合です。
都市や地図の場合、目的地が移動することはほぼ無いでしょう。しかし、友人との距離を正確に計算し、それをマップ上に経路として表示するのは非常に困難です。
なぜなら、目的地とn地点が同時に移動していることから、コストが常に変動してしまい、最適解を見つけるのに時間がかかるためです。
予想コストがどれだけ正確に計算できるかがこのアルゴリズムの肝なのです。
ゲームAIとの関係性
このアルゴリズムはゲームAIにも活用されています。
ゲーム内のエージェント(キャラクター、モンスター、NPCなど)が最短かつ最適な経路を見つけて、目的地に移動するために利用されます。
具体例
ロールプレイングゲーム:NPCや敵キャラクターがプレイヤーを追跡するときや、複雑なダンジョンをナビゲートするときにA*アルゴリズムが使われます。これにより、キャラクターは壁や障害物を回避しながら効率的に目的地へ移動できます。
シミュレーションゲーム:都市建設やマネジメントシミュレーションゲームにおいて、市民や車両が目的地までの最短ルートを見つけるのにA*が使用されます。これにより、交通の流れを最適化したり、住民の移動効率を向上させたりすることができます。
原神などでも、この技術は応用されています。パスファインディングという点では、NPCが自身のキャラクターを誘導する際に、目的地までの距離を計算して、その場所まで移動しているはずです。(すごすぎます。
まとめ
Aパスファインディングアルゴリズムは、スタート地点からゴール地点までの最短経路を効率的に見つけることを可能にします。このアルゴリズムは、ゲームAI、ロボット工学、地理情報システムなど幅広い分野で応用されており、その計算の基礎はスタート地点からの実際のコストとゴール地点までの予想コストの合計に基づいています。Aアルゴリズムの理解は、最適な経路探索を必要とするあらゆる技術分野での開発や研究において、不可欠な知識となります。
まとめ
A*パスファインディングは最短経路を効率的に探索するアルゴリズム。
ゲームAI、自動運転ロボット、GISなど多様な技術分野で応用されている。
スタート地点からの実際のコストとゴール地点までの予想コストを基に動作する。
A*アルゴリズムの弱点はゴール地点が移動する場合のコスト計算の複雑さ。
技術開発や研究において、最適な経路探索に関する深い理解が求められる。
