
ついに「2進法」が理解できた……!感動の授業をおすそ分け【高校の情報Ⅰが1冊でしっかりわかる本】
こんにちは、編集部KMです。
突然ですが、みなさんは「2進法」をご存じでしょうか。2進法とは、0と1だけで表現する数字の表し方です。0010011とか、110101とか。
たとえば私が先ほど適当に入力した「110101」は、10進法(人間が普段使っている数え方)で表現すると「53」です。
私も2進法なんてさっぱりわかりませんでしたし、日常生活の中で使うこともないので、覚える気もありませんでした。『高校の情報Ⅰが1冊でしっかりわかる本』の担当編集になることになった1年前までは……(いや、自分で企画をたてたんですが)。
そう、1年前のわたしは焦っていました。
「情報Ⅰ」の担当編集になったのに、2進法がまったくわからない。
教科書を見たら2進法について書いていたけど、2の累乗がどうのこうの言われても、「数学じゃないのになんで累乗!?」と脳みそが拒否反応をしめします(典型的な文系人間……)。
2進法が一発で理解できる、感動の授業!
そんなとき、『高校の情報Ⅰが1冊でしっかりわかる本』の著者である鎌田高徳先生から、「うちの高校の授業を見に来ませんか?」というお誘いがありました。
その日の授業のテーマは2進法。
つい先日まで中学生だったぴちぴちの高校1年生に交じって鎌田先生の授業を受けたのですが、その数十分だけで2進法が一発で理解できてしまったんです。すごくないですか?
というわけで、今日はその感動の授業をおすそ分け!
この投稿を読み終えるころには、みなさんも2進法をバッチリ理解できていることをお約束します。
点が16、8、4、2、1のカードをご用意ください
まず、点が16、8、4、2、1書いてあるカードをご用意ください。裏面は無地で。想像力が豊かな方は、頭のなかで想像するのでもOKです(でも、カードがあったほうが圧倒的にわかりやすいです!)。
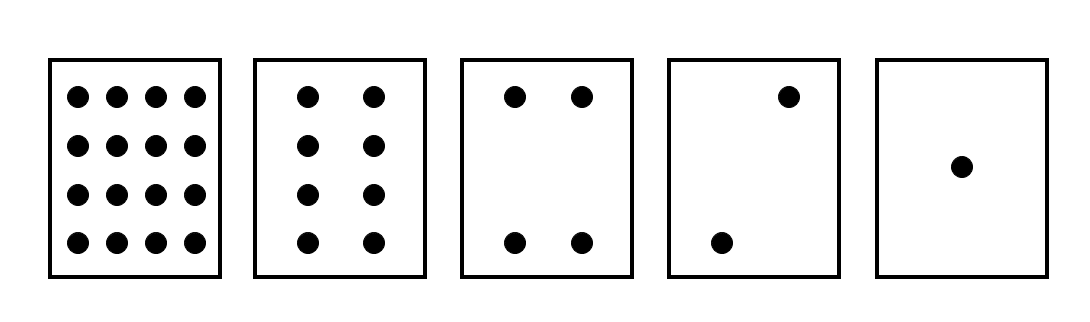
それで、このカードを裏返したり表にしたりして、見えている点の数をかぞえるんです。ちょっと練習してみましょう。
作れる一番小さい数(最小)は?
全部裏返したときなので、0です。

作れる一番大きい数(最大)は?
点が全部見えているときなので、16+8+4+2+1=31です。
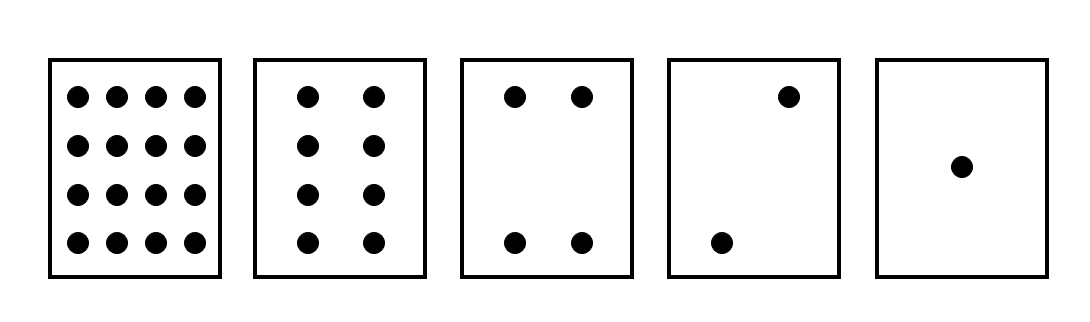
最小と最大の間の整数は、全部で何個作れる?
最小が0、最大が31でしたね。ということは、0、1、2、……、30、31なので、32個です。
ある数(たとえば15)をカードで作れるやり方は何通りある?
どの数も、1通りでしか作れません。

もう1枚カードを追加する場合、点の数はいくつ?
16×2で、32です。

そのとき作れる一番大きい数はいくつ?
↑の画像の点の数を足せばいいので、32+16+8+4+2+1=63です。
100までの整数をすべて表すには何枚カードが必要?
32の次のカードは64(32×2)になります。
64+32+16+8+4+2+1=127まで作れるので、64、32、16、8、4、2、1の7枚のカードが必要です。
「点が見えない状態」を「0」、「点が見える状態」を「1」で考える!
みなさん、だんだんわかってきましたでしょうか?
そうです、1ならカードを表、0ならカードを裏にして、見えている点の数を数えていくと、2進数を10進数に変換できるんです。
たとえば「10101」なら……

16+4+1で、21!
2進数の「10101」は、10進数だと「21」というわけです。
念のため、もう一つ練習してみます。たとえば「01101」なら……

8+4+1なので、13ですね!
2進法で秘密のメッセージを送ろう!
鎌田先生の授業ではこのあと、アルファベットと数字の対応表が配られ、2進法で秘密のメッセージをお互いに送り合って解読しよう、というワークがありました。

「love」と送りたかったら、見える点の数を「12、15、22、5」にすればいいから、

「01100、01111、10110、00101」という暗号に!
この暗号を送り合うワークで、高校生たちはとっても盛り上がっていました。暗号を作る(10進数を2進数に変換する)のも、暗号を解読する(2進数を10進数に変換する)のも、楽しいんですよね~。
やーっと2進法が腑に落ちました!
おそらく人生で何度かは2進法の仕組みに触れる機会があったと思うのですが、これまでまったく理解できなかったことが、この授業でやっと理解できました。
これからは、ちょっとだけ時間をもらえれば(頭の中でカードの点を足す時間をもらえれば)、2進数を10進数に変換できるし、10進数を2進数に変換できます。
「そうだったのか!」が詰まった1冊です
『高校の情報Ⅰが1冊でしっかりわかる本』は、2進法以外にも、「そういうことだったのか!」がたくさん詰まった1冊です。3人の登場人物の会話で話が進んでいき、ときには手を動かしながら学べるので、小さな感動がたくさんあるはず。
「情報Ⅰ」は2025年の共通テストの出題科目にもなるということで、「何から勉強を始めたらいいの……っていうか情報って何……?」と困惑している方も多いと思います。
そんな方が「情報Ⅰ」の基礎を学ぶのにピッタリの1冊ですので、ぜひお手にとってみてください!
最後までお読みいただき、ありがとうございました!(編集部KM)
