
野口広『カタストロフィーの話』と小林康夫『君自身のアートへ』

——現代数学の社会的応用』
NHKブックス272、日本放送協会発行、
昭和51年12月30日 第1刷発行、
昭和53年6月1日 第3刷発行
Amazonで購入した古書。
今からもうふた昔以上前、「カタストロフィー」という言葉にとり憑かれていた頃があり、藤岡市立図書館で見つけた野口広『カタストロフィーの話——現代数学の社会的応用』(NHKブックス、日本放送協会発行、昭和51年12月30日 第1刷発行)を借りて、フランスの数学者ルネ・トムの「カタストロフィー理論」を知った。その難解な数学的理論には理解が及ばないものの、第二話で紹介されていた「ジーマンのおもちゃ」に興味を持った。noteでの「写真集《KOBE/1995.3.》」の記事で、小林康夫氏の近著『君自身のアートへ』を引きながら、「カタストロフィー」について少し書いたので、もう一度、この本を見直したいとAmazonで検索すると、古書が安価で販売されていたので購入した。鉛筆でいたるところに傍線や波線が引かれており、前の持ち主の勉強の跡がうかがえる。
「ジーマンのおもちゃ」は1973年、東京で行われた「多様体とこれに関連した話題」というテーマのトポロジー国際学会に、イギリスの数学者ジーマン教授が携えた、カタストロフィー理論を分かりやすく説明するための簡単な玩具で、この本には図と作り方が掲載してあり、あの当時、自作してみた。20年以上も前のことを、届いたばかりの古い本を見ながら反芻する。
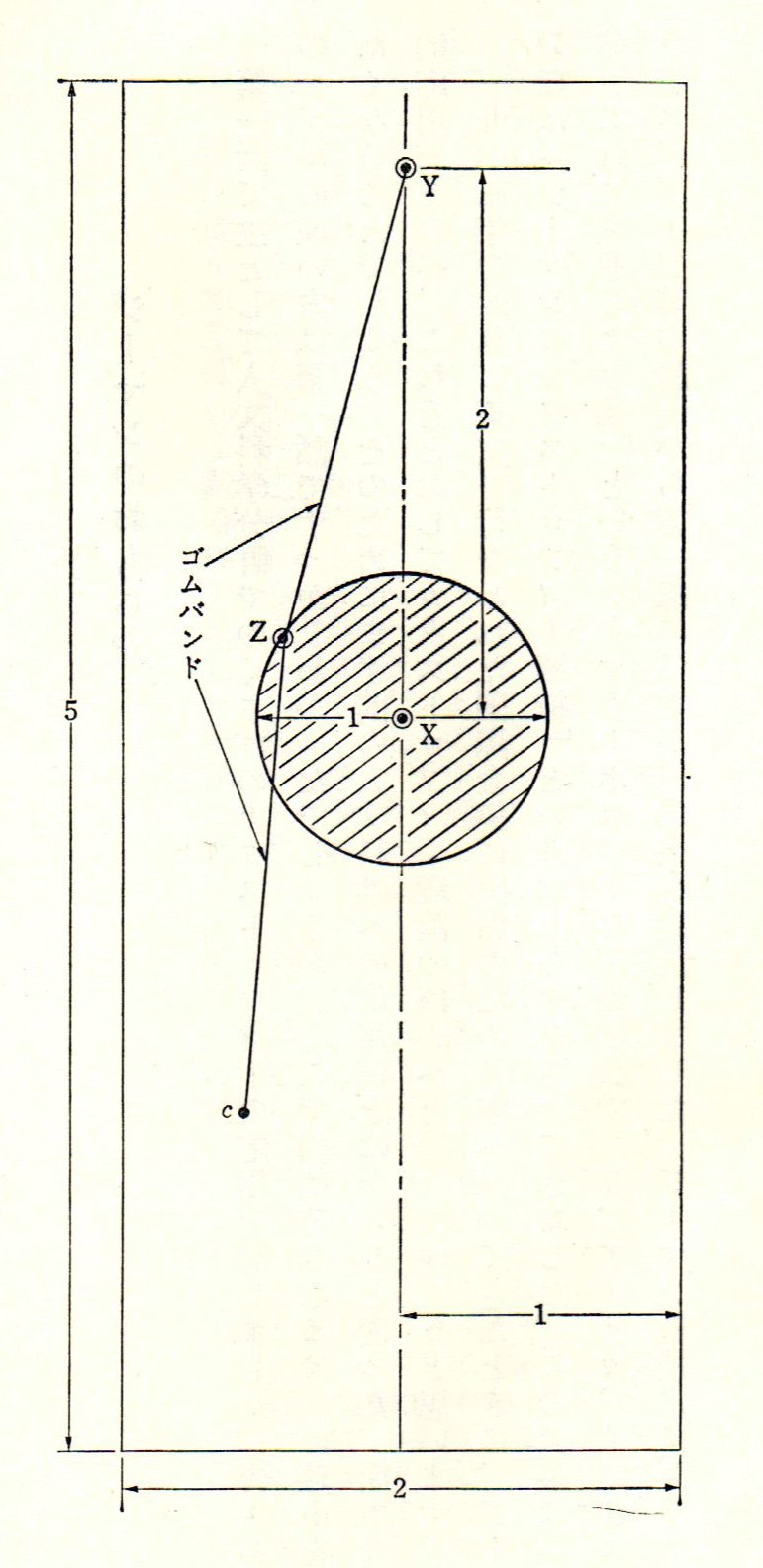
▼作り方
(かつて自身で工作したように文章を変更)
輪ゴムを伸ばさず平たく畳んで、その長さを「1」という単位とする。ボール紙で、長方形の台紙を縦「5」×横「2」の長さに、次に直径「1」の大きさの円板を制作する(円板の直径と輪ゴムの長さが同一)。台紙の中心よりやや上方の位置「X」と、円板の中心に穴を空け、小さなボルトを下から通し、台紙と円板とをナットで固定する。このとき、円板が自由に回転できるように、円板の穴はボルトより少し大きめにし、円板の上下にワッシャーを入れるとよい。Xより上方「2」の位置「Y」に穴を空けて下からボルトを通し、輪ゴムの一端をボルトにかけてナットで固定する。円板の任意の端「Z」に穴を空け、下からボルトを通して、「Y」に一端を固定した輪ゴムの他端と、もう一本の輪ゴムの一端とをナットで固定する。もう一本の輪ゴムの他端「c」を引っ張って、円板が自由に回転できるように、「X」と「Y」に取り付けたナットを緩めて、ボルトの長さを調整する。これで完成。
▼おもちゃの実験
(文章を変更)
「Z」にかけた二本の輪ゴムを伸ばした状態で、二本目の輪ゴムの他端「c」(これを「自由端」と呼ぶ)を竹串などで引っ張り、台紙上を上下左右にゆっくり動かす。すると円板は自由端「c」の動きに沿って少しずつ左右に回転するが、自由端「c」がある点を通るとき、円板が急に「しゃっくり」するように大きく上へ跳ね上がる瞬間がある。こうした一瞬に起こる不連続な大変化を「カタストロフィー」と呼ぶ。

カタストロフィーを起こすときの
自由端「c」の軌跡B
ここで鉛筆を用意して、「ジーマンのおもちゃ」の円板がカタストロフィーを起こす際の、自由端「c」の軌跡をプロットすると、図2のように点Pを尖端とする山型の左右対称の曲線になり、この曲線を「分岐集合B」と呼ぶ。尖端の点Pは直線「XY」上にあり、XP=1.41ぐらいの距離にある。
この本では、この単純な「ジーマンのおもちゃ」の不連続現象を、「ルネ・トムの定理」を使って延々と解析してあるが、私の理解は及ばない。この工作でひとしきり遊んだ後(自由端「c」を鉛筆でプロットし「分岐集合B」の軌跡を描くのは難しく、そこまでには至らなかった)、しばらく書棚に飾っていたが、いつの間にか捨ててしまった。
今、「カタストロフィー理論」をコトバンクで調べると、
▼カタストロフィー理論
1960年代にフランスの数学者R.トムが、現代数学のトポロジーを科学全般に応用しようとして考え出した理論。ギリシア語のカタストロフェ(上下転倒の意)から「破局の理論」ともいう。徐々に連続的に変化していく過程や状態が、ある時点で突発的、不連続的に大きな変動が起こる場合をカタストロフィーといい、トムはその要因となる個数が4個以下の場合には7つの基本的タイプしかないことを証明。さらに英国のE.C.ジーマンらと幾何学的モデルをつくり、生物学、社会学、経済学、心理学などあらゆる分野の種々の不連続的現象を説明した。
(出典 株式会社平凡社 百科事典マイペディア)
とある。「(カタストロフィーを引き起こす)要因となる個数が4個以下の場合には7つの基本的タイプしかない」とはどういうことか。ネットで「カタストロフィー理論 7つの型」と検索すると、「科学におけるカタストロフィ3(ルネ・トムのカタストロフィーの理論)」というサイトに行き着いた。「魚の楽しみを知る」という面白そうなサイトだった。
▼勾配ベクトル場で支配される自然界の現象は、その現象が有限個の状態しか持たないならば、7種類のカタストロフ型しか持ち得ない。
「勾配ベクトル場」とは何か、そもそも理解できないが、これがルネ・トムの定理らしい。そしてその「7種類のカタストロフ型」が列挙されていた。その7つは、
①折り目カタストロフ(Fold catastrophe)
②カスプ(尖った先端)カタストロフ(Cusp catastrophe)
③ツバメの尾カタストロフ(swallowtail catastrophe)
④蝶カタストロフ(butterfly catastrophe)
⑤双極的臍カタストロフ(Hyperbolic umbilic catastrophe)
⑥楕円的臍カタストロフ(Elliptic umbilic catastrophe)
⑦放物的臍カタストロフ(Parabolic umbilic catastrophe)
と呼ばれるらしい。『カタストロフィーの話』第八話「初等カタストロフィー」でも、これら7つのカタストロフィーの型が説明してあったが、②は「くさびのカタストロフィー」と呼ばれていて、「ジーマンのおもちゃ」の引き起こすカタストロフィーがその型であるようだ。

水声社、2024年12月10日第1版第1刷発行
装幀:宗利淳一
ここからnoteでの前記事《KOBE/1095.3.》に引き続き、小林康夫『君自身のアートへ』(水声社、2024年12月10日第1版第1刷発行、装幀:宗利淳一)を再びひもとこう。その「Art after Art——迷える若きアーティストたちへ」と題された最終章の第四章で、ルネ・トムの「カタストロフィーの7つの型」に倣うようにして、「君たち」が「はてしなく迷う」ためのYasuo流「迷悟7則」が、即興的パフォーマンスとして披露されている。
第一則=「私」という孤独を引き受ける
自分自身の「孤独」の「青の時代」を「通過」しよう。
第二則=繊細でダイナミックな、秘密の身体を!
「意識」ではなく「身体」で「線」を引け、指数関数的な膨大な数をこなそう。
第三則=NEO-PREHISTORY(新・先史時代)にようこそ!
この時代の人類史次元での激しい転換・変化についての自分なりの感覚!を見出そう。「私」とはひとつの「例外」であり、解決できない「謎」である、その「謎」を激しく「生きる」こと。
第四則=ノイズに耳を傾ける
「無秩序」から「秩序」が生まれる、それこそが「アート」という活動の核心となるエネルギー原理。この第四則で、数理物理学における「時空の特異点で分岐(カタストロフ)が起きる数学モデルであるカタストロフ理論」に触れられている。
第五則=〈美〉を封印する
世界は〈美〉という人間の感性的な判断基準を超えて存在(あ)る。この第五則では「7つのカタストロフ」の2番目の「カスプ・カタストロフ」への言及があり、次のように述べられている。
▼「カスプ」とは「尖点」ですから、(7つのカタストロフの)1番目の「折り目・カタストロフ」とは異なって、「折り返し」は、湾曲するカーブではなく、「尖点(せんてん)」となっています。その尖った点にこそ、わたしはアーティストの存在を託しているのかもしれません。
小林氏はこの「カスプ・カタストロフ」の「折り返し」「尖点」を、「反転・転換可能性」を意味するreversibleという言葉に重ね合わせ、自身が「二十歳前後に熱中して読んでいた」フランスの現象学者モーリス・メルロ=ポンティ最晩年の「研究ノート」での、▼「『見えるもの』と『見えないもの』とのあいだの交叉的なréversibibité(転換可能性)」についての思考を想起されつつ、▼「自分が地球という惑星に住む『人類』であるというその存在のあり方を、歴史的に、外から地球(人類)を見るような視点から見直すことが、今後のアートに託されているのではないか」、▼「アートとは、まさに『見えるもの』と『見えないもの』が交叉するところなのですから」、▼「われわれは、いま、まさに、われわれ『人類』がどのように存在しているのか、を発見し、認識しなければならない時代に差し掛かっているのですから。アートこそ、まさにその根源的な『転換可能性』を究極にまで推し進めるアクティヴィティにほかならない」と、パフォーマティヴな記述を展開されている。
第六則=アート、誰のために?
だが不思議なことに小林氏は、▼「この『折り返し』点は、君自身の外に、強いて言えば、誰も知らない外になければならない」と主張される。
▼人間は、——つまり「人間の脳は」と言ってもいいのですが——根源的に、そのような「Inside-Out」(「裏返しに折り返されていくいくつもの〈襞〉」)として自己形成を行なっています。われわれは日々、無数の〈襞〉を折り重ね、折り畳みすることで自分の存在を織っている。そして、アートこそ、カンヴァスや絵の具など外部にある媒体を通じてそのような「折り返し」が外化され、実践されるアクテヴィティです。
そしてそのようなカタストロフィックな「尖点」の外化=アート行為が、単なる「自己満足」や「趣味」に陥らないために、「誰のために?」という倫理的問いが絶えず問われなければならない、と。
▼わたしが願うのは、ただただ君自身が、けっして答えのないその問いを、それでも、自分自身に、自分のアートに、開くこと、そして答えのないその開けに君が耐えることです。/そして、あえて言うならば、そのとき、アートは限りなく〈祈り〉へと近づくのではないでしょうか?
第七則(空白)
この最後の第七則で、小林氏は、「それこそが、わたしにとっては、真正のアートの唯一の指標」=「これこそ、わたしにとっての変わることなきアートの定義」として、自著『知のオデュッセイア 教養のためのダイアローグ』(東京大学出版会、2009年)からの自己引用を掲げられる。
◉(……)すべてはひとつながりのひとつの人生である。問題はただ、その「ひとつ」を日々新たなものを求めて生きるか、過去を維持しようとして生きるか、だけである。他者からの、あるいは「遠い呼び声」に応えようとするのか、それとも誰の声にも耳をかさず、ただ自己を保守しようとするのか、はっきり言っておきたいが、アートというものは品のよい「趣味」などとはなんの関係もない。それは、つねに自己から「一歩外へ」出てすら、新しい生、そう、そうダンテのあのVita Nuova(新生)を希求する激しく燃え上がる火のことなのである。
▼今回、わたしが識らない君に向かってこのテクストを書いているうちに、この〈過激〉をこそ、ただ「私」というのではなく、その「私」が生命として存在しているこの「われわれ人類」、この「地球」という〈境域〉sphereへと、reversible、折り返さなければならないのでは、という思いが湧き上がってきたのです。そこにこそVita Nuovaの希望があるのではないか。/「第七則」と書いた後の空白に、いま、Vita Nuovaの一語を書きとめて、わたしは、すさまじいスピードで時代に追い越され、取り残されていく、二十世紀の精神の最後の〈希望〉を刻み込んでおくことにします。
第七則 振り返って、Vita Nuova!
実にpassionに満ちた舞踏的パフォーマティヴなエクリチュールは、ご本人にとっても「思いがけず」、「Vita Nuova」という言葉で締め括られた。ここに掲げられた「はてしなく迷う」ためのYasuo流「迷悟7則」を心に刻み、反芻しながら、この激しい「カタストロフィー」の時代をどのように生きればよいのか、答えなき問いを自らに問い続けよう。
野口広『カタストロフィーの話』には、第四話「生物学とカタストロフィー」、第五話「粘菌の子実体形成」という話も掲載されている。ルネ・トムは、1961年に西ドイツの博物館で蛙の発生の模型をみて、その形態の不思議さに打たれ、その感動が一つの動機となってカタストロフィー理論を考案されたのだという。この第四・五話は、「おもちゃ」のジーマン教授が考えられた発生生物学(developmental biology)へのカタストロフィーの応用についての話で、以前は読んでいなかったので、「朝勉」で読み始めてみよう。前の持ち主が引かれた踊るような鉛筆の傍線や波線に導かれて……。
