見出し画像

Unityのシェーダーで三角形/六角形タイル（HLSL）

カキレモン

こんにちは、カキレモンです。お久しぶりですね。

Unityのシェーダーで色々遊んでいたところ、面白そうな記事を見つけました。

もとの記事ではShaderGraphを使って実装しているのですが、個人的にノードベースのプログラミングは肌に合わないので普通のコード記述（HLSL）で同じことができないかいろいろ模索しました。

ShaderGraphは基本的にアルゴリズムをグラフにしているだけなので、ほとんどの部分はビルトインの関数を使って機械的に変換できます。しかし引用記事のシェーダーでは以下の２つのカスタムノードが使われており、これは自分で関数を書く必要があります。

カスタムノード①：UV座標を三角形状にタイリングする
カスタムノード②：ドメインワーピング（ノイズ生成）

そこで今回は、①の処理をHLSLに落とし込んでいくことにします。ちなみにもとの記事のカスタムノードはソースコードが公開されていますが、あえて直接は参考にしていません。

座標変換

先にノイズについて調べていたとき、偶然こんな記事に出会いました。

「シンプレックスノイズ」の項に座標を正三角形のグリッドに変換するアイデアが書かれていました。これはそのまま使えそうです。参照先の記事でも図付きで説明されていますが、本記事でも改めて解説してみます。

画像1

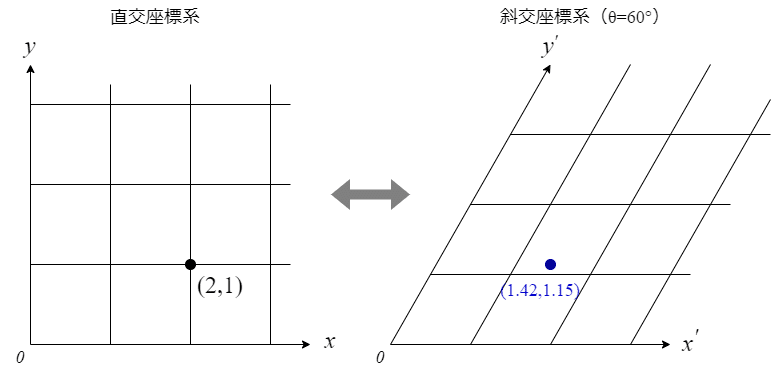
まず前提として、座標に適当な行列をかけると別の座標系に変換することができます。例えば上図では、直交座標系（図左）の(2,1)が斜交座標系（図右）でおよそ(1.42,1.15)に対応します。

座標変換の原理や意味は面倒なので深く説明できませんが、例えば碁盤を斜めから撮影したとき、写真上の座標と実際の碁盤上の座標の対応と考えると少し分かりやすいかもしれません。いずれにせよ計算自体は行列を掛けるだけなのですこぶる楽です。

三角形タイリング

さて、先の図の斜交座標系の方に注目すると、正三角形２つを繋げたタイルが並んでいるように見ることができると思います。各三角形の頂点が座標系の格子点に一致しているので、ある点がどのタイルに乗っているかは座標の整数部分に表れます。

さらに小数部分を使ってタイル内の２つの正三角形のうちどちらに乗っているかを判定します。これは「直線x+y=1に関して点（座標の小数部分）がどちら側にあるか」と考えればよく、非常に簡単に判定できます。

画像2

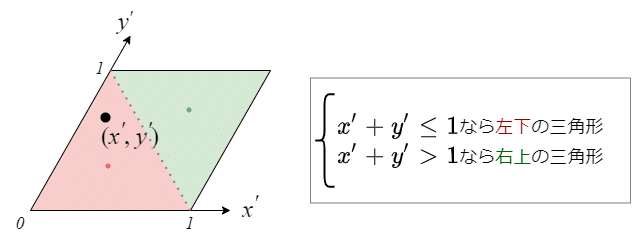
最終的に三角形の重心を返すようにしたいので、上記の判定（どちらの三角形に乗っているか）によって適当なオフセットを加算した上で直交の座標系に戻します。ちなみに三角形の重心は上の図にも小さい点で示されていて、この斜交座標系での座標はそれぞれ(1/3,1/3)、(2/3,2/3)です。

static float r3 = 1.73205080756;    // sqrt(3)の値
static float r3i = 0.57735026919;   // 1/sqrt(3)の値

// 直交<->斜交の座標変換行列
static float2x2 tri2cart = float2x2(1., .5, 0., r3 * .5);
static float2x2 cart2tri = float2x2(1., -r3i, 0., r3i * 2.);

float2 triCoordinate(float2 uv, float scale = 1.) {
   uv = mul(cart2tri, uv * scale);
   float2 index = floor(uv);    //整数部分
   float2 pos = frac(uv);       //小数部分
   
   // 三角形の重心座標を計算
   index += (2. - step(pos.x + pos.y, 1.)) / 3.;
   
   return mul(tri2cart, index) / scale;
}

最終的に、コードはこうなりました。存外に短く書けたと思っています。

六角形タイリング

六角形のタイリングも同様に座標変換を利用してやっていきます（六角形に関しても同様にr-ngtmさんがShaderGraph用のカスタムノードをすでに公開されていますが、本記事ではあくまで普通のHLSLの関数として記述することを目標にやっていきます）。

こちらでは以下をちょっと参考にしました（が、ちょっと違うアプローチを取っています）。

三角形ほど単純にはできませんでした。あまりよく考えていないのでもっと簡単な方法があるかもしれません。

三角形のタイリングの際は三角形の頂点が格子点になるように座標変換しましたが、ここでは各六角形の中心が格子点に一致するように座標変換します。

今度は１枚のタイル内に４つの正六角形が存在することになります。例によって小数部分を用いて場合分けを行うのですが、面倒なので詳細は割愛します（下図参照）。

画像3

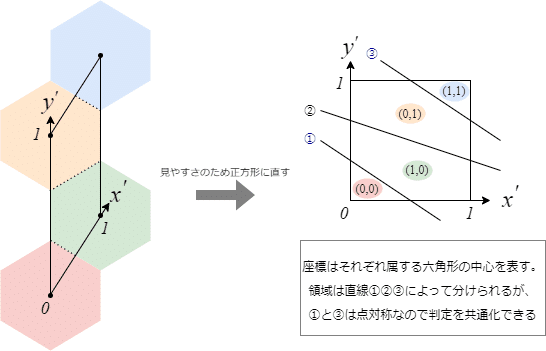
コードは以下のようになりました。

// r3, r3iの値は上に同じ

// 直交<->斜交の座標変換行列
static float2x2 cart2hex = float2x2(2, 0, -1, r3i);
static float2x2 hex2cart = float2x2(.5, 0, r3 * .5, r3);

float2 hexCoordinate(float2 uv, float scale = 1.) {
   uv = mul(cart2hex, uv * scale);
   float2 index = floor(uv);    // 整数部分
   float2 pos = frac(uv);       // 小数部分
   
   // 上半分かどうか
   float upper = 1 - step(pos.x + pos.y * 3., 2.);
   // 領域は点対称なので上半分なら折り返す
   pos = lerp(pos, 1. - pos, upper);
   // 右側の六角形に含まれるかどうか、折り返しも考慮して判定
   float right = 1. - abs(upper - step(pos.x * 2. + pos.y * 3., 1.));
   
   // 六角形の重心座標を計算
   index.x += right;
   index.y += upper;
   
   return mul(hex2cart, index) / scale;
}

使い方？

上述したtriCoordinate・hexCoordinate関数はそれぞれ受け取ったuv座標が含まれる三角形/六角形の中心座標を返します。

適当に突っ込むとこんな感じですね。（画像内のコードはフラグメントシェーダーの中身です）

画像4

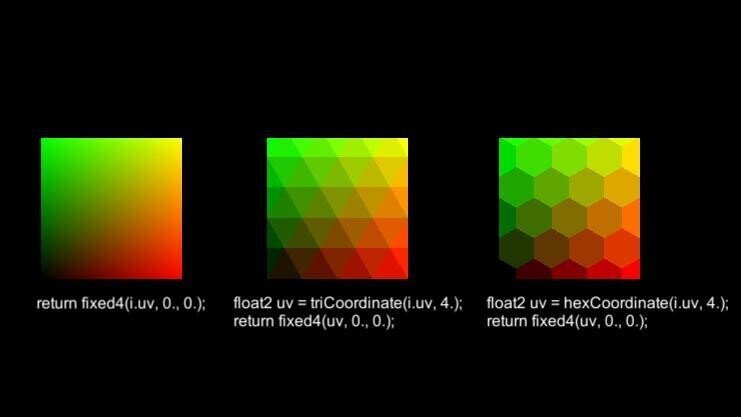
例えばタイリングしたuv座標を用いてテクスチャを貼ればいい感じのモザイク模様にできると思います。

結局やってることはr-ngtmさんがすでに公開しているカスタムノードと何ら変わりないので使い方に特に新規性はないです、すみません……

よく分かっていませんが、cgincファイルにしておくと関数を使い回せて便利かもしれません。

おわりに

いつもはPowerPointを使って作図していますが、初めてdraw.ioで作図してみました。やたら図形から矢印を伸ばそうとしたり線を勝手に近くの図形に繋げようとしたりしてくる以外は使いやすかったです。（多分これからも使うと思います。）

ちなみに今回触れなかったドメインワーピングも含めノイズに関する処理は上でも一度リンクを挙げたThe Book of Shadersで丁寧に解説されています。適当にいじるとこんな感じの模様が出ました。（左は単純にドメインワーピング、右は三角形タイリングをノイズで歪めたもの）

ということで今回は以上です。

それではまた。

この記事が気に入ったらサポートをしてみませんか？