物理でベクトル表記を使う意味
世界の果てを見せてあげよう!
白井です。ウテナっぽい登場です。
ベクトルとテンソルのお話
の続きです。
今日は、
「ベクトルとスカラ」
についてです。
ひとまずここでは、ベクトル量を図形的に
「有向線分」
と解釈しておく事にします。
スカラはベクトルに対して、
「りんごが"3"個、標高が"1200"m、電位が"-5"V」
というように、
「数量」だけの情報
を言います。
ベクトルには2つの表記方法があります。
例えば、
<a> = (a1, a2)
という
「ベクトル表記」と「座標表記」
です。
座標表記は、当然座標のとり方によってその値が変わってきます。
ここで、スカラとベクトルの根本的な性質の違いについて考えてみましょう。
例として、
山の高さと勾配(下図)
を表すことを考えてみます。
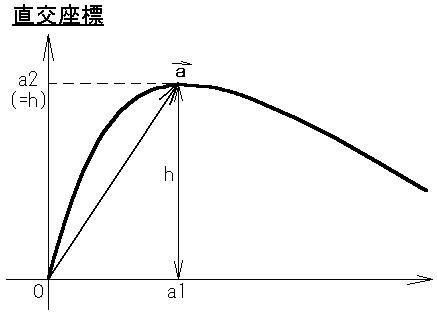
直交座標において、
頂上の地点"a"の高さが"h"
で、位置が
<a> = (a1, a2)
と表されたとします。
この場合、
高さ"h"がスカラ、位置"a"がベクトル
で、
"<a>"がベクトル表記、"(a1, a2)"が座標表記
です。
これに対して、
鉛直軸を"θ"だけ傾けた「斜交座標」
を考えてみましょう。
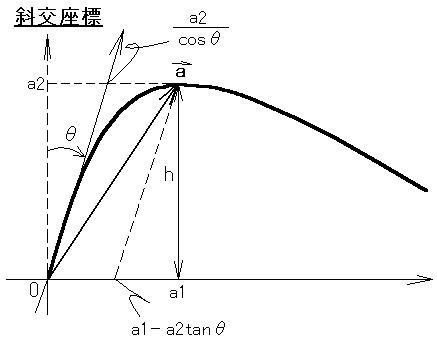
高さ"h"は座標軸に関係なく
「ある基準から何m」
とかいう風に決まっているので、直交座標のときと同じです。
ところが、位置"a"の座標表記は、軸が傾いているのでそれに合わせなければなりません。すなわち図では、
<a> = (a1 - a2tanθ, a2/cosθ)
となるのです。
つまり、
スカラは座標系によらず常に同じ値
になりますが、
ベクトルの座標表示は座標系によって異なってしまう
のです。これが、ベクトルとスカラの重要な違いです。
さて、
座標表示が座標系によって異なる
のは至極当然なことなのですが、じゃあ座標が斜交になったことで、
ベクトル"<a>"自体は変化
したのでしょうか?
No!です。
図で、
原点にあった山の位置から頂上を目指すベクトル
は変化していないことを確かめてください。(座標系の取り方によって「山が変形する」ということはありえない。)
つまり、
「ベクトル<a>」
とベクトル表示したとき、これは
座標系とは独立に存在する、普遍であるべき量
なのです。これが、ベクトル表示と座標表示の重要な違いです。
ちなみに物理の相対性原理とは、
物理法則の絶対性(座標系によらないこと)
とも言えますが、それを主張するためには「数学的表現」として、
ベクトル量はベクトル表記で記述されなければならない
のです。
ちなみに、この
「直交」→「斜交」
の座標変換を
(a1', a2') = T(a1, a2)
とすると、
T = (1, -tanθ | 0, 1/cosθ)
という「2×2の行列形式」で書かれます。これが
「テンソル」を捕らえる上での手がかり
となります。
■「行列」の表記について
テキストで行列の全要素を表記するため、
行の区切りを「縦線"|"」、列の区切りを「カンマ","」
で表すことにします。つまり、
![]()
ということになります。適宜、読み替えてください。
なお、一般的なテンソルの表記は成分表記で
η_i^j
と、
下付き添え字を"_"、上付き添え字を"^"
で表せます。
