変化ではなく状態が知りたい
経済では、財政状態の見方として、「フロー」と「バランス」というのがあります。
フローは、例えば
今月は入金が50万円、出金が45万円
というように、「収入」と「支出」という、言わば「変化」の事です。
それに対してバランスは、
今月末で現金は30万円、貯金は200万円、投資信託は500万円、ローンの支払残高は300万円
というように、「財産」と「借金」という、言わば「状態」の事です。
これはどちらも必要な情報なのですが、日々の生活ではどちらかというと、変化の方が重要になります。例えば、
「今月は収入が多かったから少しは贅沢しちゃおっか」
っていうのは、フローからの判断となります。
それに対して、
「ローンを組んで車を買おうか」
とか、
「将来のためにプログラミングスクールに通おうか」
といった、大きな金額の買い物をしたり、長期に渡る出費に関する事は、フローよりもバランスで判断することと思います。
これを間違うと、後々借金が残ったりして苦労したり、逆に安物買いとなって損をしたりすることもあるわけです。
物理量も、じつはこの「変化」と「状態」という2つに分類することが出来ます。これを意識しないと、特に熱力学では混乱してしまいます。
(何かとてもいい話をしようと思ったんですが、そこに話をつなげることが出来ず、失意のスタートです。。。)
さて前回から、熱力学の解析的手法についての話に入りました。前回の記事は
カルノーサイクルは、
( 1 )等温膨張→( 2 )断熱膨張→( 3 )等温圧縮→( 4 )断熱圧縮
という過程があります。そのため、P-V線図では「等温線」と「断熱線」だけで画けるので、これを作図してみましょう(下図)。
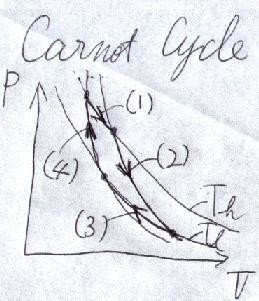
ちなみに、サイクルの線図を作図する時は、必ず
どっち向きに経路をたどるのか
を表わす「矢印」を明記しましょう。もしこれが反対向きに回っているとしたら、「カルノー冷却機」を意味してしまうからです。
上図のように、カルノーサイクルの仕事は、高熱源と低熱源の等温線と、高温と低温での断熱線に囲まれた面積になり、その熱効率は以前述べたとおり
η= (Q[high] - Q[low])/Q[high] = (T[high] - T[low])/T[high]
と簡単な形で書けました。そこで、クラウジウスはこう考えたわけです。
「P-V線図上に画かれた任意の可逆なサイクルの熱効率は、微小なカルノーサイクルに分割して計算することは出来ないか?」
つまり、下図のようにするわけです。
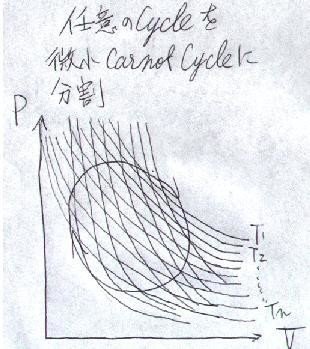
これってまさに、積分の考え方ですよね。
ところで、カルノーサイクルの特徴は、
「高熱源からエントロピー"⊿S"を受け取り、低熱源へエントロピー"⊿S"を捨てる」
ということでした。つまり、
「受け取るエントロピー」と「捨てるエントロピー」が等しい
わけです。
すなわち、微小に分割したカルノーサイクルの各区画で、
⊿S[k] = ⊿Q[k]/T[k] - ⊿Q[k+1]/T[k+1] = 0
("k"は区画の番号で、"k"番目で捨てたエントロピーは、そのまま次の"k+1"番目で受け取られる)
が成り立っています。これを極限まで微細化し、連続的な和をとれば、
⊿S =∮dS =∮δQ/T = 0
つまり、
任意の「可逆」なサイクルでのエントロピーの差し引きは"0"
になるわけです。これは、一体どういうことでしょうか?
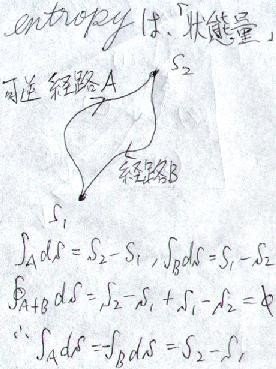
任意の「可逆過程」を組み合わせてサイクルを作ります。可逆であれば、エントロピーの差し引きが"0"になるので、
可逆な経路"A"でエントロピーを"⊿S"増やして、「別の」可逆経路"B"で同じ"⊿S"だけエントロピーを捨てる
ことが出来ます。つまり、
どんな経路であっても、可逆過程であればその経路によらず、エントロピー"S1"、"S2"という「状態」が定義できる
わけです。
それは、
エントロピーは「状態量」である
ということを示しています。
これは、力学で出てくる「位置エネルギ」が
基準点との高さの差
だけで決まり、
途中その場所まで「どう至ったか」
には依らないのと、同じように考えることが出来るということです。
つまり、ある熱的状態"A"と"B"があったら、その二つを
任意の可逆過程で結んで線積分
を行います。そうすれば、
「過渡的な状態変化」を考えることなく「結果」を吟味
することが出来るわけです。
このように、熱力学は主に、ある過程の前後の状態から考える「マクロ」な現象を扱っているのです。さらに「過渡的な状態変化」に踏みこむには、分子などの微視的相対運動や熱振動を考えねばならず、それが「ミクロ」な現象を扱う「統計力学」になるわけです。
■「状態量」「保存量」など
熱力学では、状態量とか保存量というのが良く出てきます。この二つをちゃんと理解していないと、沢山出てくる関係式を理解できなくなります。
まず「状態量」というのはその名の通り、状態を表わす量です。今まで出てきた熱力学に関する量では、
「絶対温度」"T[K]"、「圧力」"P[Pa]"、「体積」"V[m^3]"、「エントロピー」"S[J/K]"、「物質量」"n[mol]"
が状態量になります。一方、
「入熱」"δQ[J]"、「仕事」"δW[J]"
は、一般には状態量ではありません。
違いとしては、例えば状態量である温度は、制御装置などを使って「値を調整」できるものです。しかし、入熱量は「結果を測定」することしか出来ません。
物理数学的には、例えば、"Z"が"u, v, x, y"の変数であるとき、
dZ = vdu + ydx
などの全微分がとれる場合、経路に依らない「状態量」であるわけです。
「保存量」は、時間的に変化しない量ということで、例えば「定積変化」だったら、「体積"V"」が保存量になるわけです。つまり、「ある拘束条件を表わす量」ということが出来ます。
ちなみに、定積過程で熱の出入りがある場合、温度や圧力が「変化量」になります。
この辺がよくごっちゃになるところで、「保存量」は「状態量」ですが、「状態量」であっても必ずしも「保存量」ではなく、ある過程でどの量が固定されるのかという事を考える必要があるわけです。
ちなみに、「状態量」は「示強変数」と「示量変数」に分類されます。それはまた、別の機会にお話ししようと思います。
