ナウなヤングのフックの法則

　若い頃はイケイケな格好でブイブイ言わせていた白井です。

　ブイブイって何なんですかね。豚ですが？それはブヒブヒ。

　ベクトルとテンソルの話の続きで、今回はテンソルについて触れていきたいと思います。

　わだしがナウなヤングの頃は、「テンソル」というのを理解するまで本当に苦しみました。

　もちろん数学の概念なんていうのは、具体的なイメージが出来なくても使えるようにさえなればいいんです。でも、自分なりに腑に落ちる理解が出来なければ覚えることが苦痛になるんですよね。

　そこであきらめてしまったらそれまでなんですが、いわゆる「落ちこぼれる」っていうのは、それより先に進めなくなってしまう事じゃないかと思うんです。それで、先に進めた人も、実は本当に納得しているわけではないというのが、大半なのではないでしょうか。

　それでも、自分が使うだけならそれでいいんです。問題は、人に教えるときです。自分でも本当に納得していないので、「これは覚えるしかない」となってしまって、落ちこぼれる人が出てくるんだと思います。

　私にとって、「テンソル」という概念がその一つでした。

　なので、ここでの話は、入り口を無事抜け出して、

よし！じゃあリーマン幾何学の計量テンソルに挑戦してみよう！

という気持ちになるまでの理解の過程を共有しようかと思います。

　●テンソルの顔

　テンソルは、複数の「顔」を持っています。

　まず数学的な面から見てみると、

１、ベクトルの概念の拡張で、

「行列」は「2階のテンソル」

「ベクトル」は「1階のテンソル」

「スカラ」は「0階のテンソル」

と言えることです。だから、もちろん2階より上のテンソルもあって、

「3階のテンソル」

というと、

四角い箱に数字がみっちり並んでいるイメージ

です。4以上は具体的なイメージはしようもないのですが、拡張して多次元的に数が並んでいるもの、つまり数の塊です。

　もう一つの顔としては、実用的には

２、あるベクトルから他のベクトルへの「写像」を与えるもの

となります。

　「写像」というのは、前回お話しした「ベクトルの座標変換」のことです。

　ただ、

「こっちのベクトルからあっちのベクトルへ変換したよ～」

ではなんのことやらさっぱりだと思います。

　そして問題は3つ目。物理では、

３、これが具体的な物理量である

ということで、

数学的な「変換」が、何故具体的な「物理量」になるのか

というところに結び付ける理解が必要になります。

　なので、ここでは

「応力テンソル」

というものを例にとって考えていきたいのですが、まずこの「応力」についてお話します。

　●応力とは

　一般的な物体は、力を加えると変形します。

（高校物理の力学の範囲では、変形をほとんど扱わないので「剛体」というものを考えていますが、これは理想的なものです。）

　バネを考えてもらうとわかりますが、

変形すると元に戻ろうとする力

すなわち「弾性力」が発生します。

　バネの場合は「縮む」ということがはっきりと目で見てわかるのですが、例えば固そうな鋼鉄の内部にも、

微視的にバネのような機構

があって、力を加えれば変形して弾性力が生じます。この内部に発生する力を「内力」といいます。

これは具体的には、強制的な変形に対する、

物体を構成する原子や分子同士の反発力

になります。

　内力は、下図のようなイメージです。

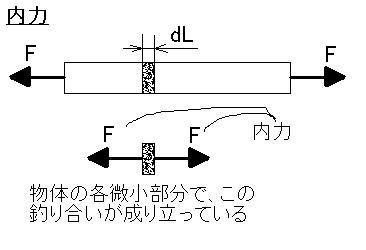
　棒を長手方向の軸と平行に引っ張る

とします。このとき棒全体では、

大きさが"F"で等しく、互いに逆向きの力

同士で釣り合っています。

　ここで、

仮想的に微小部分"dL"で切り取ってやった

とすると、やはり

同じ釣り合いが成り立っている

のです。

　さて、この内力による物体の「変形」を考えてみましょう。

　変形に関係するのは、内力の大きさだけではありません。同じ力をかけても、

太い棒は変形しにくく、細い棒はすぐ変形して

しまいますね。つまり、

力を受ける断面の面積

が関係している訳です。

　応力と言うのは、この

物体の変形に関係した量

のことで、

内力を断面積で割った値

σ= F/S

で定義されます。

単位面積当たりの力である「圧力」

と同じ単位で [Pa]（パスカル）になります。

　また、変形する量も、

長い棒では大きく伸びますが、短い棒ではあまり伸びない

ということで、

変形量を元の長さで割った値

ε= δL/L

を考えてやります（下図参照）。これを「ひずみ」と言います。

（長さを長さで割っているので、単位はありませんが％で表したりします。）

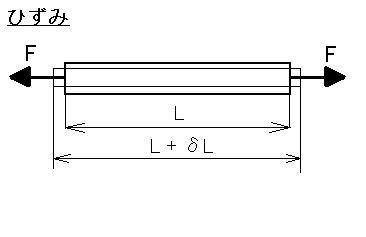
　「応力」と「ひずみ」。これは材料力学での基本的な物理量となります。

　この二つの間には、次のようは比例関係が成り立ちます。

σ= Eε

これを、「フックの法則」と言います。

（ちなみにバネのフックの法則

F = kx

と同じ形ですが、ホントはバネの方は正確には成り立たなくて、

この近似が出来る範囲で使用する

ということになります。）

　"E"は「ヤング率」と言って、

ひずみによって発生する応力の比率

を表し、硬いものほど大きくなります。

　それでは、ザギンにシースーイークーなので、この辺で。