やっと見えたエントロピーの顔の一部
「顔の一部」と言ってもメガネではありません。(古い)
さて、熱力学の歴史とエントロピーの概念について、自分なりに調べたことを整理して書き綴っていて思うことがあります。それは、改めてこの概念は、いろいろな側面からアプローチすることによって、やっと全体像が見えてくるものだという事です。
エントロピーに限らず、数学や物理の理論は、確かに「結論」は一つです。しかし、その結果をどう捉えて、現実の事象をどう説明していくのかというのは、人により様々です。
裏を返せば、多種多様で複雑に見える現実の事象も、実はその裏に横たわる根本原理は同じであり、極度に抽象化された仮説により、それを見出すことが出来るということを示唆していると思います。
さて今回は、トムソンが考えた絶対的な温度の基準から、エントロピーという概念が導かれるまでの経緯を、考えてみたいと思います。
前回の記事はこちら
トムソンの考えた温度目盛はこういう物です。もう一回、「カルノーサイクル」を復習すると、
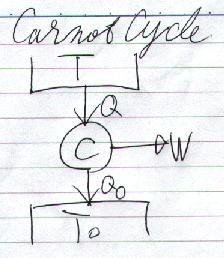
もらった熱は"Q"、捨てた熱が"Qo"。で、行った仕事が、
W = Q - Qo
という、サイクルで吸収した熱がそのまま仕事になるサイクルでした。このとき熱効率"η"は、
η= (Q - Qo)/Q = (T - To)/T --- ( 1 )
と書けました。さて( 1 )式を次のように変形します。
1 - Qo/Q = 1 - To/T
↓
Qo/Q = To/T
↓
T/To = Q/Qo --- ( 2 )
一体これは何を表しているか?
カルノーは、
「熱源の温度差が大きければ大きいほど、熱効率が大きい」
と言っています。これはこう言うこともできます。
「熱源の温度差は、吸収した熱量が大きいほど大きい」
つまり( 2 )式は、
温度の「比」を、カルノーサイクルが熱源からもらった熱と捨てた熱の「比」で「定義」した式
ということになるのです。
これが「熱力学的温度目盛」というものです。これによって、物質によらず、理論的に「温度差」が導けることになりました。
つまり"To"として何か基準を定めてやれば、全ての温度がこれで決まります。
では基準を何にするのか?
という話ですが、実は「絶対温度」らしきものは、
V = bT(気体の体積が温度に比例する)
という「シャルル(ゲイリュサック)の法則」から定義されていて、
低圧、低温の極限で
PV/T = 一定
という「ボイル・シャルルの法則」が成り立つならば、
絶対零度 = -273.15℃
である事が測定によってわかっていました。
トムソンは熱力学的温度目盛が、「理想気体」のときのこの目盛と同等であることを示し、現在では
「水の三重点」の温度(摂氏0.01度、圧力0.611kPa)
を
To = 273.16K
としています。
さて、ちょっと先を急いで、( 2 )式をさらに変形すると、
Q/T = Qo/To
となり、これは
「熱源とやりとりした熱"Q"」と「そのときの温度」の比が一定
であることを示しています。カルノーサイクルにおいては、この
Q/T
という量が不変になるのです。
1865年、クラウジウスがこれに、「エントロピー」と名付けました。これが、エントロピーの概念の発見です。(「エントロピー(entropy)」は、ギリシア語の「エネルギー(energie)」と「変化(trope)」を合わせた造語です。)
さて改めて、「等温過程」でやり取りした熱を"⊿Q"、その時の温度を"T"と書くと、やり取りしたエントロピー"⊿S"は、
⊿S = ⊿Q/T
と書けます。「カルノーサイクル」ではつまり、
高熱源から"⊿S"をもらい、低熱源に"⊿S"を捨てた
のです。
カルノーは、
「仕事は、カロリックの高熱源から低熱源への移動によってなされる」
と言いました。つまり、
カルノーの言う「カロリック」とは「エントロピー」の事
だったのです。カルノーサイクルの熱効率は、逆に、先にこのエントロピー"S"という量があると認めてしまえば、
Q[high] = T[high]⊿S, Q[low] = T[low]⊿S
より、
η= (Q[high] - Q[low])/Q[high]
= (T[high]⊿S - T[low]⊿S)/(T[high]⊿S)
= (T[high] - T[low])/T[high]
となります。これが実はカルノーサイクルのもう一つの特徴で、熱効率を最大化するサイクルは他にも沢山あるのに、何故カルノーサイクルが基本に置かれるのかも、ここに理由があります。
実際はクラウジウスは、トムソンの仕事を見てこれを考えたわけではないので、ここでは別のアプローチを取っている事になります。
クラウジウスは、この"Q/T"という量が、熱力学的過程の可逆性の指標になると考えました。
次回は、クラウジウスの仕事を見てみたいと思います。
