座標とともに変わる物差し
突然ですが,みなさんおでんの具は何が好きですか?
私ははんぺんが好きです.〇ブン〇〇ブンで,おでんの保温器にぷかぷか浮いているはんぺんを見ると,暑い日でも食べたくなってしまいます.
ということで今日は,ベクトルの「共変」「反変」の話です.
前回までの記事は,
テンソルとは一体どういうものかという事を,
「応力」の概念
を使って簡単に説明したわけですが,あの議論の中では
どういう座標系か
ということを考慮していませんでした.もっと言うと,
「3次元ユークリッド空間」(線形でベクトルの内積が定義できる)
で,
「デカルト(直交)座標系」
を主に想定したものでした.
実は,直交座標系を設定して考えられる問題に対しては,テンソルの概念のありがたみはあまりありません.テンソルがその本領を発揮するのは,
曲がった座標系を考えるとき,さらには曲がった「空間」を考えるとき
なのです.その「曲がった座標系」を考えるには,
「反変」「共変」という考え方
が必要になります.今日はそれについて考えていきます.
例によって,まず
2次元の「斜交座標系」
で考えてみることにします.
何か新しい概念を考えるときは,
一番単純なモデルで考えてみる
と良くわかります.
「空間」よりも「平面」,「曲線」よりも「直線」
という風にして,
その概念が必要になる最小限の要素まで次元を落としていく
と,本質が見えやすくなります.(もちろん,そこから「一般形」を類推していくことも大切です.)
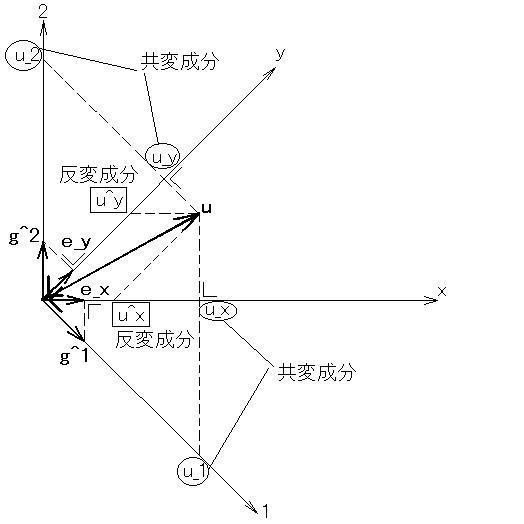
[Fig.1](画像だけ別ウィンドウで表示すると便利です)
Fig.1のように
"u"というベクトル
があり,
x軸とy軸が斜交した座標系
を設定したとします.
"e"は「x-y斜交座標系」に固定した単位ベクトル
で,
この座標系で"u"を計った目盛り
を,
(u^x, u^y)
と表すことにします.これを、「反変成分」と呼びます。(理由は後でまとめて説明します.)
ここで,
u^x
と書いたのは,「"u"の"x"乗」ということではなく,
"x"の添字を上に書いている
ということです.また,
x軸とy軸に垂線をおろしたところの目盛
を
(u_x ,u_y)
とします.これは,「共変成分」と呼ばれるもので,さっきとは逆に
下付き添字
で表します.
さて,反変成分の方は,
平行四辺形の性質
から単位ベクトルを使って,
u^ = u^x e_x + u^y e_y
と,ベクトル"u"を表現することができます.("u^"と書いたのは,x-y座標系で見て反変成分で表されていることを示しています.)
しかし,
共変成分ではこのような表現ができない
事は,視覚的に確認できると思います.
そこでちょっと工夫をして,Fig.1のように
「y軸に直交するように1軸」
「x軸に直交するように2軸」
というふうに
新たに斜交座標系を設定
してやります.そうすると図のように
共変成分と,新たな1-2座標の基底ベクトル"g^1", "g^2"
を使って,
u~ = u_1 g^1 + u_2 g^2
と書けます.("u~"と書いたのは,1-2座標系で見て共変成分で表されていることを示しています.)
ここで,
"u_x"と"u_1"または"u_y"と"u_2"のつくる三角形
に注目して頂きたいのですが,それぞれが
基底ベクトル "e_x"と"g^1"、"e_y"と"g^2"によってつくられる三角形と相似
になっていることが確認できます.すなわち
長さの比が
e_x : u_x = g^1 : u_1
e_y : u_y = g^2 : u_2
となっていて,
「"u_x", "u_y"というのは,x-y座標系で単位ベクトル"e_x", "e_y"で計った目盛の値」
「"u_1", "u_2"というのは,1-2座標系で基底ベクトル"g^1", "g^2"で計った目盛の値」
であるので,値としては
u_x = u_1
u_y = u_2
ということになっています.このように,
x-y座標系から1-2座標系に座標変換
した時,
基底ベクトルに合わせて共に変化して行く成分
という意味で「共変成分」と呼ぶのです。
それでは"u^x", "u^y"はどうかというと,この成分は
「x-y斜交座標系」のみで通用する成分表示
であって,そこから仮に,
「1軸」「2軸」に垂線を下ろしていく
とすると(図示していないので頭の中で下ろしてください),その値は,
基底ベクトルの長さに反して小さい値になっている
事が分かると思います.こういう,
ある座標系に固有の成分量
で,座標変換に伴う
「基底ベクトル」の変換に反した変換をされる成分
ということで,「反変成分」と呼びます.
そろそろおでんが食べたくなってきたので,次回はもうちょっと別の極座標の例で具体的に考えていきたいと思います.
