やっぱり温度って不思議

　なんか考え始めると、その思考の周辺で思いつく色々な事も気になって、いつのまにかフォーカスがシフトしてしまい、間にいろいろ違う話題がはさまりがちになっています。私の悪い癖ですね。

　しかし、改めてアウトプットというのは、それだけで学びの切っ掛けになりますね。この note は、過去に私が得た気付きをまとめる為に始めたつもりなんですが、数年経ってまとめ直すと、今の視点で新たな気付きがまた出てくるんです。

●アウトプットを意識したインプットが大事

　またまた余計な話ですが、最近、

知識のインプットばかりでなくアウトプットが大事

という話を聞いたりするんですが、まずはやはりインプットが無いと、そもそもアウトプットが出来ません。しかし、重要なのは、

インプットの仕方

なんです。さらに、質と量の問題もありますが、

量を「こなし」ながら質を高める

が正解です。ただ大量にインプットするのに、「こなす」も何もないと思うかも知れませんが、

アウトプットを意識しながらインプットする

という事をやっていると、インプットもかなり集中力が必要です。

　そして、よく

「メモが大事」

という話も最近言われていますが、要するに、「メモを取る」という行為は、

インプットした知識の即席アウトプット

なんです。だから、メモの本質は

アウトプットを意識してインプットする事

であって、「殴り書き」でも「板書写し」でもないんですね。

　逆に、頭の中でアウトプットのための整理が出来ていれば、「書く」という行為自体必須ではないんです。ただ、そんなことをできる人は、よほど頭の回転が速い人なのでしょうけど。

　のっけからいきなり盛大に話が逸れてしまいましたが、「ジュールトムソン効果」の話の続きです。

　「ジュールの実験（断熱自由膨張）」と「ジュール・トムソンの実験（断熱搾り膨張）」を紹介しました。そしてこの実験では、

気体の膨張に伴い、気体の仕事に関係なく温度が低下する場合がある

ということでした。そのメカニズムを、分子論から考察してみたいと思います。

●内部エネルギの中身

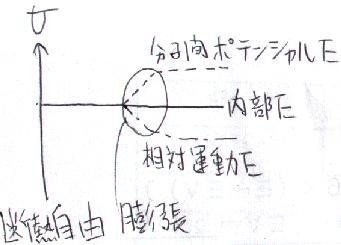
　内部エネルギーの「中身」を分子論的に見ると、

（内部エネルギー）=（分子間の相対的な運動エネルギ）+（分子間距離によるポテンシャルエネルギ）

という事になります。「温度」に関係するのは、このうち「運動エネルギ」の方であると言う話がいわゆる「分子運動論」です。

　一方、体積膨張に関しては、「ポテンシャルエネルギ」が関係してきます。

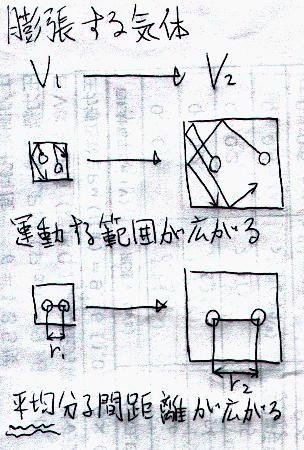
　「膨張」と一口に言っても、「気体」は「固体」のように

ただ寸法が大きくなる

という感じではありません。気体では分子がもともと激しく運動をしているので、その

運動の範囲が広がる

つまり、

分子間の「平均距離」が広がる

と考えるということになります（下図）。

　分子間距離が広がるということは、「分子間のポテンシャルエネルギ」が増加するということです。つまり、ジュールの「断熱自由膨張」の実験では、

外部に仕事をしていなくても「分子間引力」に対して仕事をして

いて、

その分「相対的運動エネルギ」が減少している

わけです（下図）。

　よって、

分子間力の働く「実在気体」

では、

　相対運動のエネルギが形として表れている温度が下がる

のです。この現象は、

分子間力の働かない「理想気体」

では説明が出来ません。

●ジュールトムソンの実験と温度の正体

　また「ジュール・トムソンの実験」では、

（エンタルピの変化）－（分子間ポテンシャルの増加）＜０

となるとき、温度が低下する

ということが言えます。

　何故、温度が低いとこれが負になるのかというと、

温度が低い時は内部エネルギーが小さい

ので、分子間のポテンシャルエネルギが小さく、

膨張した時の「ポテンシャルエネルギの増加」が大きい

からです。

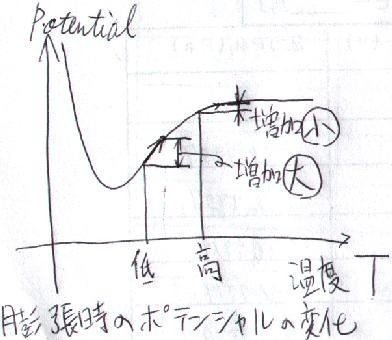
　分子間力によるポテンシャルが、何故こういう曲線になるのかは、「分子間力」のイメージについてまた記事を書きたいと思います。

　温度が「上がる」場合の話ですが、この実験を厳密に説明するには、「実在気体の状態方程式を理解する必要があります。「逆転温度」に対しては当然「逆転圧力」という見方も存在するわけで、「P-T曲線」上に現れる「逆転曲線」で表わされます。

　ただ、完全にイメージだけで言うと、

気体の温度と圧力が高い

場合、

温度が高いのでもともと分子は激しく運動をしたい

のですが、高い圧力で一定の体積に圧縮されているため

広い範囲で運動できずに押し込められている

という事になります。そして、

体積が増えると、熱運動できる範囲が広がって、運動が激しくなる

という感じです。

　ところで、気体分子運動論をかじっただけだと、

「圧力」も「温度」もどちらも「分子の運動」によるもの

という感じがするので、膨張して圧力が下がるのに、温度が上がるのは不思議な感じがするのですが、この

ジュール・トムソン膨張で温度が上がる

という現象は、

温度と圧力が本質的に異なるもの

という事を示していると言えます。

　確かに温度というか、熱の伝わり方は「接触（熱伝導）」だけでなく、「電磁波（熱輻射）」もあります。

　つまり、圧力は微視的には

分子の運動の力学的現象

であるのに対して、温度は

電子の運動も関係する電磁気学的現象

でもあるわけです。

　改めて、温度というものは不思議なものだと感じます。

●ジュールの直観と先見性

　ここで、分子間力の働かない理想気体について考えます。分子間力が働かなければ、当然

自由膨張しても温度が変化しない

ので、内部エネルギを

U = U(V, T)

と考えると、ジュール・トムソン過程は「断熱過程」であり、

U(V1, T) = U(V2, T)

であるので、

(∂U/∂V)t = 0

　つまり、等温下での体積変化では、「内部エネルギー変化」は無い事が言えます。これを「理想気体のジュールの法則」と言ったりします。

　十分「希薄」な気体は分子間力も弱く、理想気体とみなせる

ので、

希薄な気体でジュールの実験を行えば、温度変化は無い

わけです。またジュールの法則より、

理想気体の内部エネルギーは、「体積」には依存しない

ことが言えます。

　ここで疑問なのは、

「断熱過程で仕事をしないなら、内部エネルギーの変化が"0"であることは直観的にもわかりそうなのに、ジュールの一連の実験では何を明らかにしようとしたのか？」

ということです。前にも書いた通り、

「熱の仕事当量の実験」でもジュールは、水の粒子間の摩擦を予想していたかのような実験を行いました。この頃はまだ、

「気体の分子論」は認められていなかった時代

であり、内部エネルギは、「温度変化」によってしかその表象を捕らえることが出来なかったわけです。

　このジュールの実験も、まるで

ファン=デル=ワールスの唱えた「分子間力」を先駆けて予想していた

かのような実験に思えます。

　ジュールは父親の造り酒屋を継ぎ、大学には所属せず、生涯、学者にはなりませんでした。しかし学者にはない鋭い洞察力で、熱学の理論を先駆ける素晴らしい実験を沢山行ったのです。

　また、ジュールはとても好奇心旺盛で、新婚旅行の時に滝を見て、

「滝では水が落下するので、滝の上よりも下の滝壺のほうが温度は高くなるであろう。」

と考えて、なんと持っていた温度計で測定を始めたというエピソードが残っています。しかし、性格はとても控えめで、亡くなる前に、

「私はちょっとしたことを二つ三つやったけれど、どれも大したことではない。」

という言葉を残したそうです。

　私も、ジュールのような学びの心を忘れない技術者でありたいと、改めて思わされました。