切り口で見え方が変わるのが応力

　缶コーヒーのことを，「缶コーシー」っていう人いますよね．あれって何かの方言でしょうか？元ネタが気になります．

　どうやら白井です．「応力テンソル」の話です．

　前回の記事はこちら．

　前回は，応力には

「垂直応力」と「せん断応力」

があり，せん断応力は，

外力の働く方向と斜めの方向のにとった仮想断面に現れる

ということでした．

　ここで，おや？と思った人がいるでしょう．

　仮想断面はあくまでも「仮想」なのであって，

物理的に意味があればどんな方向に断面を取ったって自由

なわけです．

それぞれの応力の値は断面の取り方で決まる

ので，これでは

応力一意に定義できなくなってしまいます（下図）．

　そこで，発想の逆転をした人がいました．それは，

断面によって変換されるような量

として，応力を定義してしまおうというものでした．その人は，

フランスのA. L. コーシー

です．

　コーシーは，関数解析ではこの人の名前の付かない定理を探すのが難しいくらい有名ですが，もともとは工学屋さんで，Ecole Polytechique の土木科卒業です．つまり，

変形体を扱う力学が専門

だったんですね．

　ところで，応力とは何度も言うように，

外力に対しての反発力として存在

するもので，その総和は

外力と逆向きのベクトル量

となるはずです．

応力を断面によって決める

ためには，

断面と応力ベクトルを対応させる

必要があるわけです．

　断面は

断面の「法線ベクトル」

で決まります．そこでコーシーは，

「法線ベクトル」と「応力ベクトル」を対応させよう

と考えたわけです．概念としては，

応力を調べたいある検査面が決まると，その面の法線が決まり，

その面の法線ベクトルを，回転，伸縮させて変換する

のです．その

変換の演算子のことを「応力テンソル」と呼ぶ

ことにしたのです．

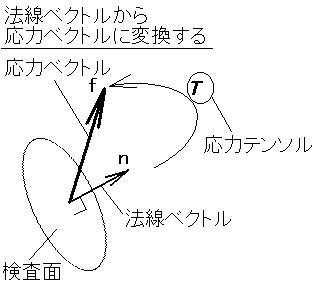
　すなわち上図では，

f = T n

ということになります．具体的な演算の中身は，

応力テンソル"T"が「行列」の形

で書けて，

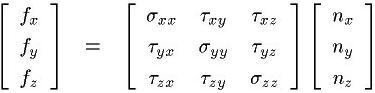
ということになります．

　テンソルの成分は，このように

添字がついた量

で表されます．この場合は

2つの添字がついているので，「2階のテンソル」

といいます．

　ちなみに，一般に

「n階のテンソル」は「(n-1)階のテンソル」の変換

という性質を持っています．しかし，この

「変換の演算」というのは，テンソルにとって1つの性質

なのであって，

それ自体が方向性を伴う実在量

であり，「テンソル」というのはそういった量の「総称」ということなのです．

　「変換」のことを「テンソル」というのではない

のです．

　また，ベクトルの

「ベクトル表示」と「成分表示」の話

と同じように，上の2つの式で，

テンソル"T"と書くのと「行列形式」で書くのでは，普遍性が全く違い

ます（以前のテキストを参照）．

　それは，

ある面の法線ベクトルとそこに働く応力ベクトルが座標系によらない

ならば，

その関係もまた座標系によらないもの

であるべきだということなのです．

　以上がテンソルの物理的な意味になります．

　さて，話が一段落したので，コーシーでも飲みますかね．