真っすぐ切るかナナメに切るか

　そういえば、前に「ななめ45°」っていうお笑いグループがあった気がする白井です。

　今回も応力テンソルに向けて応力の話ですが、「せん断応力」について考えます（一つの文章に「応力」という単語が３つも出てくる文章クオリティ。）

　前の記事はこちら、

●もう一度応力について

　もう一度説明すると、例えばある棒の軸方向に、

大きさが等しくて向きが正反対の力"F"が働いている

とします。当然、

この2つの力は釣り合って

いて、棒は止まっています。

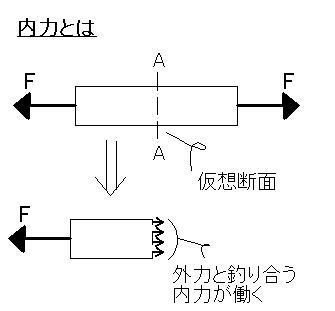
　いま、仮想的に"A-A"という断面を考えると、

ここにも外力"F"と釣り合う力が働いている

はずです。（もしここに何も力が働いてなければ、棒は加速度を持って動き出す。）

　これが棒に働いている「内力」で、

「内力」をその断面積で割った値が「応力」

というのでした。

●軸応力とせん断応力

　さて、応力には2つの種類があります。

　断面に垂直に働く「軸応力」

と、

断面に沿って働く「せん断応力」

です。

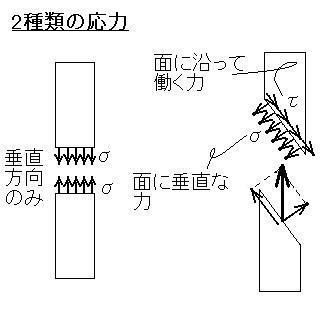
先ほどは、断面を

軸と垂直な方向（すなわち外力と垂直）

に取ったので、上図のように

そこに働く応力は断面に垂直な成分だけ

になります。

　ここで、

軸を斜めに切る断面

を考えてみましょう。

そこに働く内力を断面に投影

してやると、図のように

断面に沿った方向の力

が現れる事が分かります。

　変形する連続体を扱う分野では、

この断面に垂直な方向の応力を"σ"と書いて「軸応力（又は垂直応力）」

断面に沿った方向の応力を"τ"と書いて「せん断応力（又は接線応力）」

と言います。

　この2つの応力を2次元で考えると、下図のようになります。

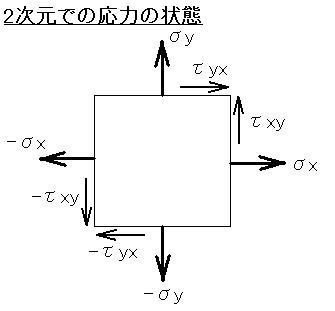
ここで、"τxy"には2つの添字"xy"がついていますが、これは

"x"軸に垂直な、"y"方向のせん断応力

ということを表しています。"yx"だったらその逆です。

　ちなみに、この応力は、

釣り合って物体が静止していることが前提

だったので、

「力のモーメント」も釣り合っていて、

τxy = τyx

ということになります。

●断面によって働く力が変わる？

　ここで、ある疑問が湧いてきます（湧かしてください）。

　断面の切り方なんて無数にあるけど、じゃあ本当に働いている応力はどれを考えればいいの？

　実は、この

断面の取り方こそが座標の取り方

なのであって、取る座標系によって応力の見え方が変わる

のです。

　しかし、

断面の取り方で応力が変わるわけではない

というのが、物理法則の要請です。

　ではその

不変の応力はどうやって表すか

というと、それそこが「応力テンソル」

なのです。

　次回はいよいよ、この応力を組み合わせた

「応力テンソル」

について考えていきたいと思います。

　「はい、ななめ45°」