小学1年算数　大胆提案！「数の合成・分解」は深追いするな！

１年生教科書では、１から１０までの数を習った後勉強するのが「数の合成や分解」です。
「２と３で〇」（合成）や「５は２と〇」（分解）というものです。
これが一部のゆっくりちゃんにとってとんでもなく難しい！
保護者にしてみれば、我が子が１年生になって２か月ぐらいで勉強につまずくことに驚愕してしまいます。

つまずく理由
１．数字という概念の未定着
２．言語的理解の難しさ
３．カリキュラム設計の不適切さ（これって結局足し算と引き算を頭の中でやらせようとしているよね問題）

・・・などが考えられます。

理由１．数字という概念の未定着

数の合成・分解をすばやく処理するには、
「〇〇〇〇〇」＝「５」＝「ご」
という「数量」と「数字」と「読み」が同等のものとして脳内で変換しながら操作できなくてはいけません。
大人になるとこれら３要素がしっかり統合しているので暗算や読み上げ算などを行うことが可能ですが、ゆっくりちゃんの中にはこれらのつながりが未熟な子がある程度います。
数量・数字のつながりが弱い子もいれば、数字と読みのつながりが弱い子もいます。
1から順番に数えないと数が認識できない子もいます。

まずは、子どもがどの数でつまずいているのか確かめる必要があります。
数字カードと数図ブロックをつかってクイズを出してみるとわかります。

「数量⇔数字⇔数の読み方」を統合させる練習

数字と数量・読みの統合　指導例

１～１０の数字カードの中から１枚（ここでは７）ランダムに提示し
「この数なーんだ？」と問います。
子どもが「なな」と答えられたら、その子の中で数字と読みが統合していることがわかります。
次に「ブロック７こちょうだい」と要求します。
ちゃんと７個渡すことができたら、その子の中で数量もしっかり統合して認識していることがわかります。
できなければ、正解を教えて、また時間をおいてから繰り返し強化していけばいいでしょう。

数量と読みの統合　指導例

子どもに１～１０の数字カードをわたしておきます。
教員が数図ブロックを提示し、「この数なーんだ？」と問います。
「７」のカードを示し「なな」と答えることができればその子の中で数字と読みは一致しているといっていいでしょう。

ポイントは、ゲーム感覚で楽しみながらやることです。慣れてきたら、子どもに出題者役をやらせてみてください。より理解が深まることでしょう。

理由２．言語的理解の難しさ。

ゆっくりちゃんの中には「５は３と２」「３と２で５」という言葉をしっかり理解できない子も多いです。なんせ数日前に０～９の数の書き方を学んだばかりの子が、いきなり３つの数の入った文の理解を求められるのだから。
誤解を恐れず言うなら、「できない子が悪い」のではなく「問い方が悪い」ということです。
言葉での理解が難しい子には、はじめのうちは指導者が数図ブロックを提示したりその一部を手で隠したりして「いくつ？」など易しい言葉で問いかけるのがよいでしょう。

数の合成　指導例

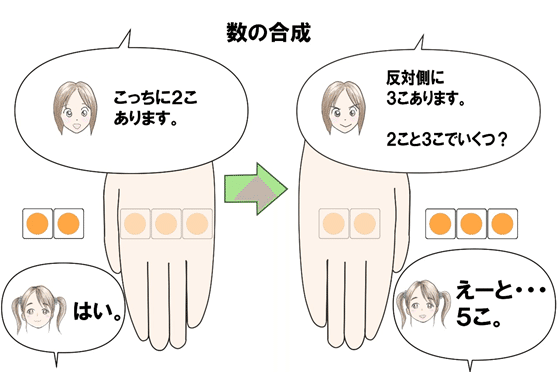
ここではまず、５この数図ブロックを机に並べ両手で隠しておきます。
まず右手で隠したブロックを提示し、子どもが「２こ」あることを確認したら再度隠します。
次に左手で隠したブロックを提示し、「３こ」あることを確認したら再度隠します。
そして、「２こと３こでいくつ？」と問えば、今見たブロックの数をイメージしながら答えることができます。

これは別々に見た２と３を脳内でイメージし、くっつけあわせることで「数の合成」の理解につながります。
それでも間違えてしまう子には、繰り返し右手と左手のブロックを交互に見せてあげれば答えやすくなると思います。

数の分解　指導例

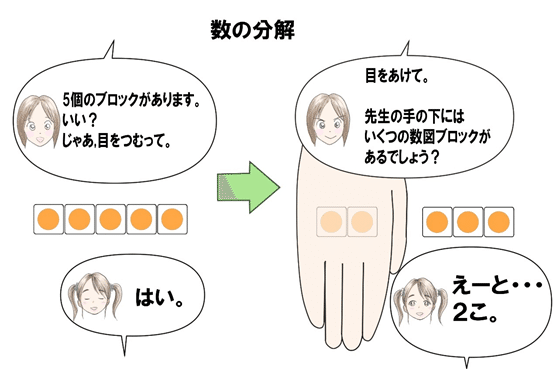
ここではまず、机の上に５個のブロックを並べて提示し子どもと数を確認します。
子どもに目をつむってもらい、その間に２この数図ブロックを手で隠します。
手で隠されたブロックの数を先ほどの記憶からイメージしながら答えることができます。

これは、５という数が２と３に分けられるという「数の分解」の理解につながります。
それでも間違えてしまう子には、最初からもう一度やって記憶を強化することで、答えやすくなると思います。

いずれも、クイズのような感じで楽しみながらやっていき、段階的に数や問い方にバリエーションを加えていけば、ゆっくりちゃんも楽しみながらステップアップしていけることでしょう。

理由３．カリキュラム設計の不適切さ（これって結局足し算と引き算を頭の中でやらせようとしているよね問題）

この単元では、たとえば「８は〇と２」（分解）や「５と３で〇」（合成）というような問題を見かけます。
難しいですね～。

「これって、まだ習っていない引き算と足し算をいきなり暗算でやらせているよね？」とツッコんでしまいます。
子どもは、遊びや生活の中で物の数を数えたり、いくつか加えたり引いたり数えたりしながら、生活経験の中で数概念を獲得していきます。
にもかかわらず、教科書では足したり引いたりする経験より先にこの分解と合成が先に学習します。

先生によっては、できるようになるまで図のような「さくらんぼ算」を何枚もプリントに刷って繰り返し練習させる方もいます。

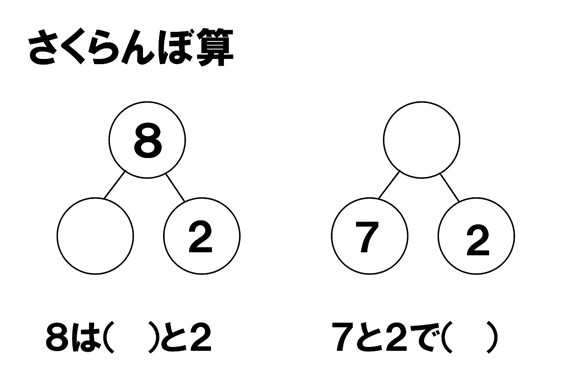
これで分かる子はいいですけど、苦手な子にしてみたら、算数嫌いになる苦行でしかありませんね。

はっきり言ってこれらの学習が理解できていなくても足し算、引き算はできるようになります。
数図ブロックや指などの具体物を実際に増減させ答えとなる数を「１，２，３，４・・・」と数えればいいんです。
こうした指導はガチンコ算数教育者から「序列」と「数量」を混同した「数え主義」として忌み嫌われることが多いです。
しかし、私は前述のとおり、数を物の数を数えたり増やしたり減らしたりするということは、数概念を経験的に学ぶ重要なプロセスだと考えています。
おそらくあなただって、未経験の言語で「１０は２と何？」と尋ねられたら「アン、ドゥ、トロワ、カトル・・・」や「ハナ、トゥル、セ、ネ、タソ・・・」と数えるでしょう。
真の学びとは、生活と教科的な学習事項を子ども自身が認識の中で経験的につなげていくことであって、系統的カリキュラムを順序通りマスターさせることではありません。

まとめ

正直なところ私としては、まだ数概念に不慣れな子に、「数の合成・分解」で過度に時間を費やすのは反対です。
大胆な提案ですが、「数の合成・分解」は深追いしてはいけません！

ここでつまずく子には、軽くスルーさせて次の足し算に進んだ方が理解しやすいと思います。

数図ブロックや指、お金等の具体物を使って増減させたり実際に数えたりしながら計算に慣れ親しんだ方が楽しく分かりやすく学習が進められると考えています。