
「丸」と「三角形」は同じ?
今回は久しぶりに数学の話題!
いわゆる「トポロジー」について書いてみるが、私も全然詳しくないので間違えているところがあればご教示ください。
そして今回は数式はほとんど使いません。
使ったとしても中学校の範囲までとします。
また、使う際は随時説明も入れますので、前提知識もそこまでなく読めます!
「円」と「三角形」は同じなのか?
まあ普通に考えて「そんなわけない!」と思うと思います。
それは当然で、普通に考えると三角と円は全然違うものです。
ここで問題となるのは
「何をもって同じとみなすのか?」
ということです。
少し中学校で習ったことを思い出してみましょう。
図形が合同であるとは?
以下の画像を見てください。
二つ三角形がありますがこれらは同じものでしょうか?

大きさも形も同じ
「なんか回転とかして移動させればぴったり一致しそうだから同じ!」と思われた方が多いと思います。
さて、
「図形を回転、ひっくり返す(対称移動)、平行移動させる」ことでぴったり一致する2つの図形を合同といい≡の記号を使って表します。
この考え方を導入すれば二つの三角形は
合同である
と言えそうです。
そしてこれは形や大きさが同じという意味で
同じ図形!と言えそうです。
図形が相似であるとは?
また以下の画像を見てください。
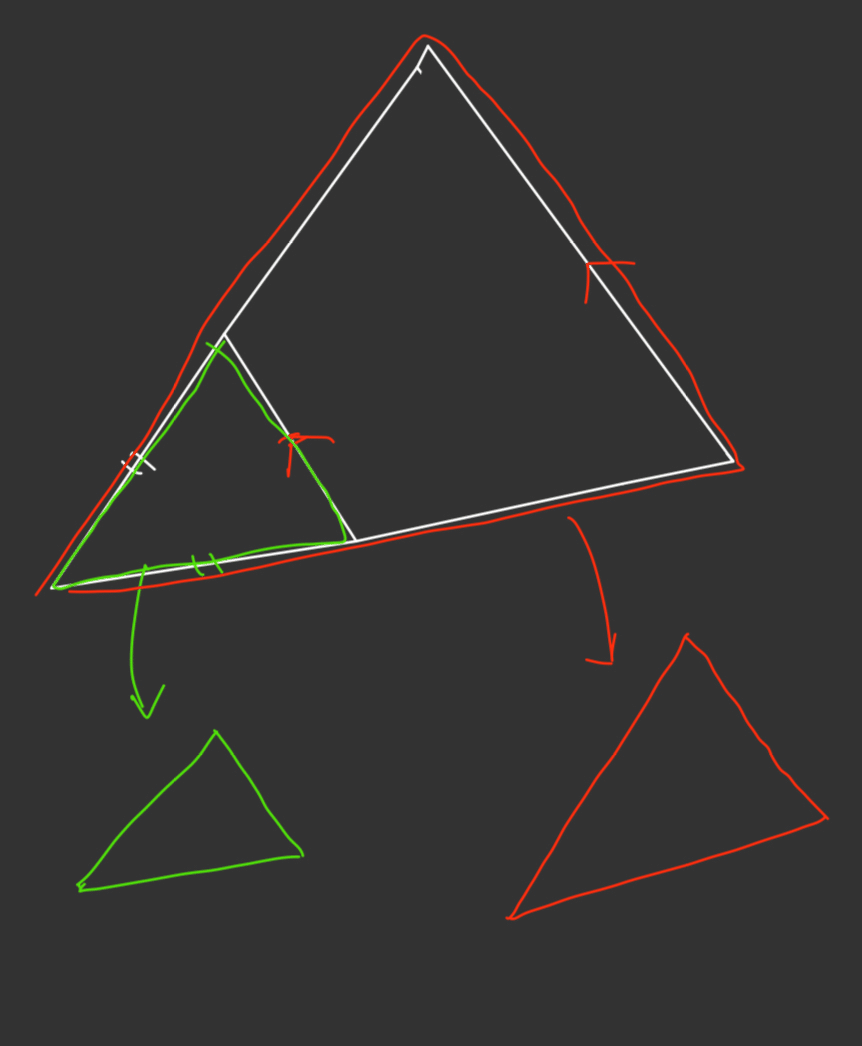
次は形は同じですが大きさは違います。
これは同じと言えるでしょうか?
「図形を拡大、縮小」すれば合同となるものを
相似といい∽で表します。
この考え方を導入すれば二つの三角形は形が同じ(つまり相似)という意味で同じと言えそうです。
図形が同相であるとは?
またまた以下の画像を見てください。

次は形も大きさも違います。
これは流石に同じとは言いにくいです。
でも数学ではこれも同じと言える武器があります。
それが同相です!
厳密には写像や位相などの理解が必要ですが、今回のコンセプトとは外れるので感覚的な説明を
まず、輪ゴムをイメージします。
輪ゴムは当然「輪」ゴムですから円です。
しかし上手く形を変えてあげると三角形を作ることもできます。
このように「破ったりせずその形を再現できるなら」同じものとするのが同相です。
ですので、円とハート型は同相ですし、四角形も同相です。
今までは平面で考えてきましたが立体でも同じです。
これを使うと「取って付きのマグカップとドーナツは同相だ!」という主張もなんとなく理解できるかと思います。
あとがき的な
今回は全く厳密性を考えずに書いてみた。
まあこれはこれで良いのかなと思う。
「円と三角形が同じ!」と主張するのは無理でしょう。となるのは分かるが、それは「同じという基準をどう取るかで変わる!」というのがこの問題の本質だった。
数学をしているとこのように概念を抽象化していくことがよくある。
今回なら合同は一番具体化された例で
合同、相似、同相
の順に抽象化されていった。
私は現代文がそこまで得意でなかったから「具体」と「抽象」は全然わからなかった。
だが、今数学をしてて「抽象化する」ってすごく大切なことなんだと気付いた。
もちろん全てについて具体化して議論することが出来たら一番良い。
だが、一般にそれは現実的ではないから抽象化した概念について議論を行う。
これは考えてみれば至極当然のことでなぜ今までこんなことに気付けなかったのだろう...と感じた。
抽象的なものを理解するのは非常に難しい。
その時は具体例を見ると分かりやすいし、評論などでは「抽象」→「具体」→「抽象」の流れになっている。
私の好きな本で「数学ガール」シリーズの中で主人公は「例示は理解の試金石」とよく言っているがまさにその通りだと思う。
もう少しつけ足すと
中学校などで習う「文字式」も抽象化されたものだった。
公式もある意味でそうだろう。
今の教育で「主体的・対話的・深い学び」が謳われている。
全科目の中で数学はこの目標に対して取り組むのが難しい方だと思っている。
(数学と聞くと苦手な意識を持ってしまう人も多いから...)
でも、数学を数学のままとだけ捉えず、色々なことを学べるとも思えば、まだほんの少しだけでもマシになると思う。
私も塾などで教える時は気を付けていきたい。
10/11(水)変更
タイトルと一部見出しを変更致しました。
御指摘ありがとうございます。
