
特徴的な写像であるプロジェクション【高校数学の延長】
中学数学や高校の数学で使われているのですが、用語をはっきりと習わないものがあります。
集合の直積です。
定義をはっきりと認識すると理解が深まります。
大学の数学の入門的な本には定義が明確に書かれていますが、高校生の段階で認識している人は少ないです。
▼目次
・直積の定義と例
・プロジェクション
集合の直積というあまり聞きなれない数学の用語ですが、算数や中1数学から既に使われています。
実数全体を集めてできる集合をRと書いておきます。
中1の数学で習うxy座標平面、実は集合Rと集合Rの直積集合です。
【直積の定義と例】
集合Aと集合Bがあったときに、この2つの直積集合をA×Bと表します。
この直積集合の要素は(a, b)という形の組になります。
ここで、aはAの要素、bはBの要素です。
A×Bの左から1番目の集合がAなので、(a, b)の組の1番目がAの要素ということを表します。
3つ以上の集合についても同じように直積集合が定義されます。
A×B×C×Dの要素は(a, b, c, d)というようになります。
[例]
xy座標平面のときは、(3, 2)というように2や3はRに含まれる実数となっています。
算数の場合の数の単元でも、直積集合が使われています。
2つのさいころAとBを振ったときの出た目を(1, 5)のように表したりします。
Aのさいころの目が1で、Bのさいころの目が5ということです。
数字でなくても、直積集合は算数や中学数学で習います。
箱Aにリンゴが3個、箱Bにミカンが2個入っています。Aから1個、Bから1個それぞれ果物を取ります。
このときに、集合A = {リ1, リ2, リ3},集合B = {ミ1, ミ2}としておくと、
直積集合A×Bの要素は次の6個になります。
(リ1, ミ1), (リ1, ミ2), (リ2, ミ1),
(リ2, ミ2), (リ3, ミ1), (リ3, ミ2)
場合の数の単元では、6通りの場合があると呼ばれます。
【プロジェクション】
直積集合 A×B の要素である組(a, b)について、1番目のaのことを第1成分(component)、2番目のbのことを第2成分といいます。
このときに、組(a, b)から1番目の成分を取り落とす写像(関数)のことをプロジェクション $${p_1}$$、2番目の成分を取り落とす写像をプロジェクション $${p_2}$$ といいます。
[例]
先ほどの2つのさいころの出た目について説明します。
A = {1, 2, 3, 4, 5, 6},
B = {1, 2, 3, 4, 5, 6}とします。
このとき、直積集合A×Bができます。
文字を使って正確に表すと,
A×B = {(i, j) | i∈A, j∈B }
6×6で36個の要素から成ります。
プロジェクションで取り落とすとどうなるかを書きます。

第1成分を取り落とすか、第2成分にするかということが記号で表せました。
xy座標平面でプロジェクションをすると、座標軸に影がつきます。
第1成分へのイメージ図です。
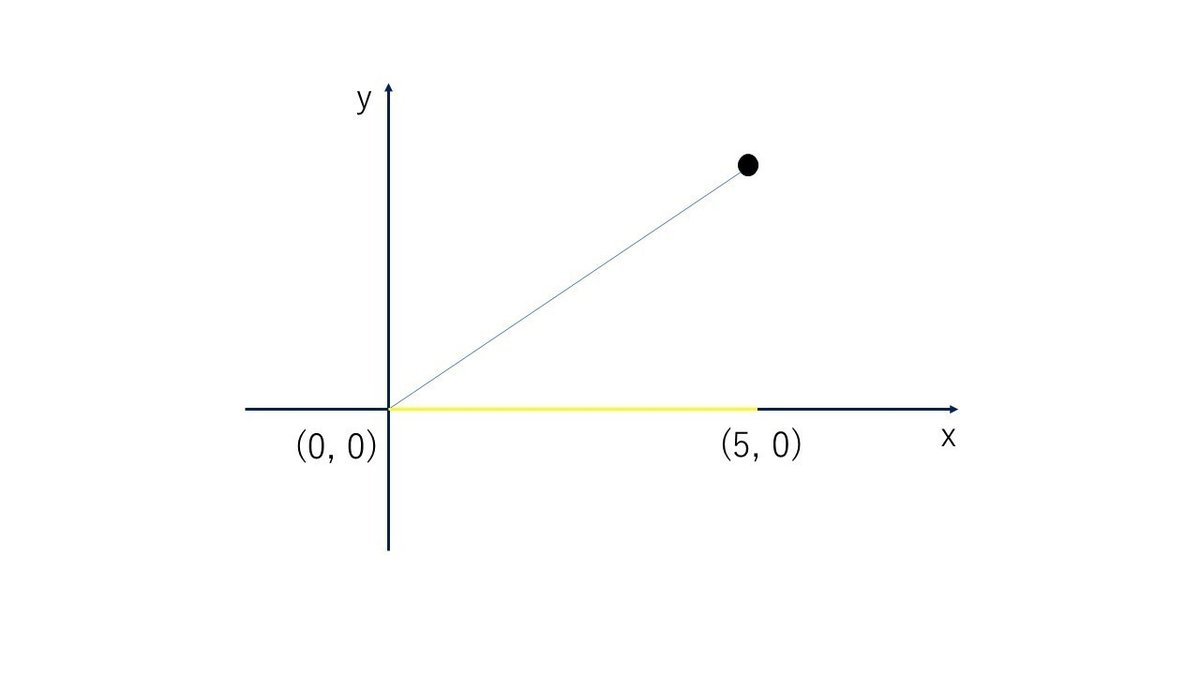
このプロジェクション(射影)は、数学や物理で、しばしば使われます。
分数やマイナスやルートがあっても、同じく影を落とすことができます。
$$
p_{1}\biggl(\displaystyle\frac{2}{3},\,-\sqrt{2}\biggl)=\frac{2}{3},\,p_{2}\biggl(\displaystyle\frac{2}{3},\,-\sqrt{2}\biggl)=-\sqrt{2}
$$
関連する記事として、数学IIIの微積の内容の記事を投稿しています。
タロウ岩井の"岩井の数学ブログ"というサイトになります。
シンプルな具体例で定義の内容をつかんでから、理論の構築へ!
