
o1-previewに日本数学オリンピックの予選問題を解かせてみた
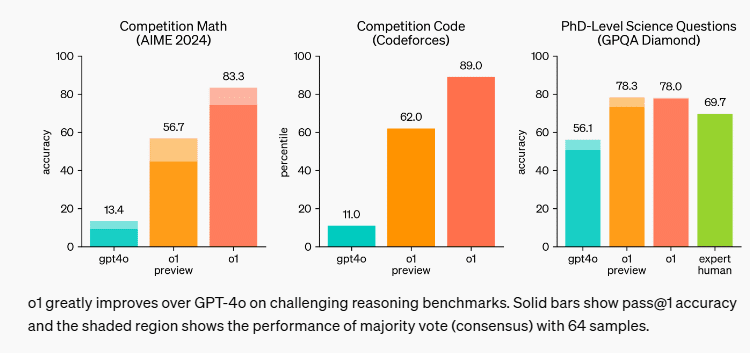
OpenAIの最高性能の推論モデルo1(未公開)のアメリカ数学オリンピック予選(AIME)の正解率は83.3%、o1-previewの正解率は56.7%でした。但し、これは64サンプルの多数決の結果で、1回限りの回答だと、o1-previewの正解率は40%程度(濃いオレンジ色の部分)に落ちます。
今回は、実際に今年1月に行われた2024年日本数学オリンピック予選の問題をo1-previewに解いてもらうことにしました。
なお、2024年予選の決勝進出基準は12点満点の6点で、最高得点は10点でした。(1問1点で部分点無し)
第1問

以下の値は有理数である。これを既約分数の形で表せ。 √((123! - 122!) / (122! - 121!))

筆者のコメント:正解です。
解き方も問題ありません。
第2問

どの桁に現れる数字も素数であるような正の整数を素敵な数とよぶ。3桁の正の整数 nであって、n+2024と n−34がともに素敵な数であるものはちょうど2つある。このような nをすべて求めよ。


筆者のコメント:正解です。
素敵な数となるxを全部リストアップして力づくで計算しています。スマートに解くには、まずxの一の位に注目して、8を足した時に一の位が素数になる素数は5と7のみ。次に十の位に注目して、6を足した時に一の位が素数になる素数は7のみというように絞り込んでいきます。
第3問
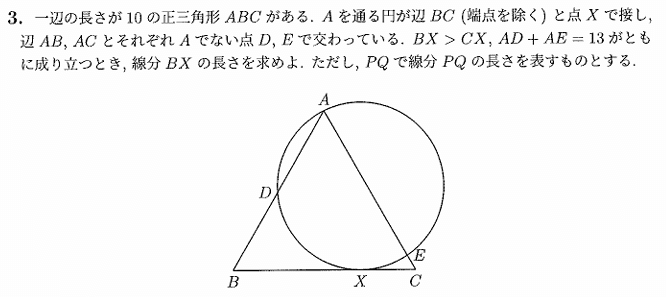
一辺の長さが10の正三角形ABCがある。Aを通る円が辺BC(端点を除く)と点 Xで接し、辺AB, ACとそれぞれAでない点D, Eで交わっている。BX>CX, AD+AE=13がともに成り立つとき、線分 BXの長さを求めよ。ただしPQで線分PQの長さを表すものとする。


筆者のコメント:不正解です。正解は$${5+\sqrt{10}}$$です。
BX=x, BD=yとおき、$${BD・BA=BX^2}$$、$${CE・CA=CX^2}$$の方べきの定理を使って、連立2次方程式の解を求めます。
【o1-miniによる回答】

筆者のコメント:正解です。
途中の面倒な計算を省略していますが、答えは合っています。
第4問

nを0以上5^5以下の整数とする。黒石n個と白石5^5−n個を横一列に並べ、次の操作を5回繰り返す。
石の列を左から順に5個ずつ組にする。各組に対して、その組に属する5個の石を、それらの5個の石のうち多い方の色の石1個に置き換える。
最初の石の並べ方によらず、最後に残る1個の石が必ず黒石であるようなnとしてありうる最小の値を求めよ。



筆者のコメント:不正解です。正解は2883です。
全体の石の数$${5^5= 3125}$$個から最後に白石となる場合の最も少ない白石の数$${3^5=243}$$個を引いて1個足すと2883個になります。
なお、この問題は、o1-miniも解けませんでした。
第5問

10以上の整数nであって、
[n/1][n/2]…[n/10]=nC10
をみたすようなもののうち、最小のものを求めよ。ただし、実数rに対してr以下の最大の整数を[r]で表す。たとえば、[3.14]=3、[5]=5である。

筆者のコメント:不正解です。正解は2519です。
$${_nC_{10}=(n/1)\{(n-1)/2\}\{(n-2)/3\}・・・\{(n-9)/10\}}$$であり、これが[n/1][n/2]…[n/10]と等しくなるためには、n+1が2から10までの数で割り切れればよい。したがって、nの最小値は$${LCM(2,3,4,・・・10)-1=2^3・3^2・5・7-1=2520-1=2519}$$です。
なお、この問題は、o1-miniも解けませんでした。
第6問

AB=AC=5なる二等辺三角形 ABCの辺AB上にAD=3をみたす点Dが、辺BC上 (端点を除く)に点Eがある。点Eを通り直線ABに点Bで接する円をωとすると、ωは三角形 ADEの外接円に接した。ωと直線AEの交点のうちEでない方をFとすると、CF=10が成り立った。このとき、辺 BCの長さを求めよ。ただし、XYで線分 XYの長さを表すものとする。


筆者のコメント:不正解です。正解は$${\frac{14\sqrt{65}}{13}}$$です。
なお、この問題は、o1-miniも解けませんでした。
第7問

次の条件をみたす 3 以上の素数 p と 1 以上 2024 以下の整数 a の組 (p, a) の個数を求めよ。
a < p^4 であり、ap^4 + 2p^3 + 2p^2 + 1 が平方数となる。

筆者のコメント:不正解です。正解は16個です。
第8問

非負整数に対して定義され整数値をとる関数 f が、任意の非負整数 m, n に対して
f(m + n)^2 = f(m|f(n)|) + f(n^2)
をみたしているとき、整数の組 (f(0), f(1), ..., f(2024)) としてありうるものはいくつあるか。

筆者のコメント:不正解です。正解は$${2^{990}+1}$$個です。
f(0)=0の場合はf(n)=0の定数関数で1通りのみですが、f(0)=2の場合は、nが奇数かつ平方数でないときにf(n)=2の場合とf(n)=-2の場合があり、$${2^{990}}$$通りの組があるので、合計$${2^{990}+1}$$個となります。
第9問

円に内接する四角形 ABCD があり、AB=7, BC=18 をみたしている。∠CDAの二等分線と辺BCが点Eで交わっており、また線分DE上の点Fが∠AED=∠FCDをみたしている。BE=5, EF=3 のとき、線分DFの長さを求めよ。ただし、XYで線分XYの長さを表すものとする。

筆者のコメント:不正解です。正解は17/3です。
第10問

100×100のマス目の各マスにJ,M,Oのいずれか1文字を書き込むことを考える。2×2 のマス目であって次のいずれかをみたしているものを良いブロックとよぶこととする。
- その4マスに書き込まれた文字がちょうど1種類である。
- その4マスに書き込まれた文字がちょうど2種類であり、その2種類の文字はそれぞれ 2つずつ書き込まれている。
- その4マスに書き込まれた文字がちょうど3種類であり、左下と右上のマスに同じ文字が書き込まれている。
このとき、次の条件をともにみたすような書き込み方はいくつあるか。
- どの2×2のマス目も良いブロックである。
- 辺を共有して隣り合う2マスの組であって書き込まれた文字が異なるのはちょうど 10000組存在する。ただし、マスの順番を入れ替えただけの組は同じものとみなす。
ただし、回転や裏返しによって一致する書き込み方も異なるものとして数える。

筆者のコメント:不正解です。正解は$${_{198}C_{100}・3・2^{100}}$$です。
第11問

正の整数に対して定義され正の整数値をとる関数fはf(34)=2024をみたし、かつ任意の正の整数a, b, cに対して、3辺の長さがそれぞれ
a+f(b), b+f(c), c+f(a)
であるような三角形が存在する。このとき、f(100)+f(101)+⋯+f(199)としてありうる最小の値を求めよ。ただし、同一直線上にある3 点は三角形をなさないものとする。


筆者のコメント:不正解です。正解は102050です。
第12問

次の条件をみたす 0 以上 2099 以下の整数の組 (a1, a2, ..., a2100) の個数を求めよ。
整数の組(b1, b2, ..., b2100)であって、任意の1以上2100以下の整数iに対して
ai≡∑(bj) (mod 2100) (ただし、gcd(j - i, 2100)=1, 1≦j≦2100)
となるものが存在する。ただし、右辺はj−iと2100をともに割りきる2以上の整数が存在しないような1以上2100以下の整数jについてのbjの総和である。


筆者のコメント:不正解です。正解は$${\frac{2100^{210}}{2^{164}・3^{30}}}$$個です。
2024年日本数学オリンピック予選問題の解答解説のリンク
まとめ
(1) 問題のテキスト化
今回、問題の画像をChatGPTのGPT-4oにアップロードし、以下のプロンプトでテキスト化しました。
この問題をlatexを使わないで書き写して
こうして問題をテキスト化したことにより、今後は簡単にLLMに数学オリンピックの問題をテストすることができます。興味のある方は利用してみてください。
(2) テスト結果
o1-previewの性能の高さを見せようと思ってテストしたのですが、結果は12点満点の2点(正解率16.7%)という低い成績に留まりました。OpenAIの公式サイトでは、アメリカ数学オリンピックの予選でo1-previewが56.7%の正解率(64サンプルの多数決)を達成したと書かれていたのですが、それよりもかなり低い数値となりました。
これは、日本の数学オリンピックの予選問題の方が難しいのでしょうか、それとも、思考時間の制約やモデルの調整などテストした条件に違いがあるのでしょうか。なお、日本数学オリンピックの予選問題は後の方になるほど難しくなり、最後の問題は、ほぼ誰も時間内には解けません。
o1-miniは、o1-previewの解けなかった第3問を解いたので、o1-previewよりも数学の性能が高い可能性があります。
図形問題を解く場合にすぐに座標計算に頼るなど、o1-previewは力づくで問題を解こうとする傾向があり、あまり数学のセンスはよくありません。数学オリンピックの問題を解くには、もう少しひらめきなどが必要です。
o1の正式版は、o1-prebiewよりも数学の性能がかなり高いようなので、それだと数学オリンピックでどのくらいの点数が取れるのか、リリースの発表が待ち遠しいところです。
