韓・伊理のp97のジョルダン標準形
今日も今日とてジョルダン標準形。今日は韓・伊理のp97の行列。我が家にある手計算でジョルダン標準形にできるものはこれで最後となります。
固有多項式は普通に計算すればよいようでした（出だしも途中も迷いまくった）。
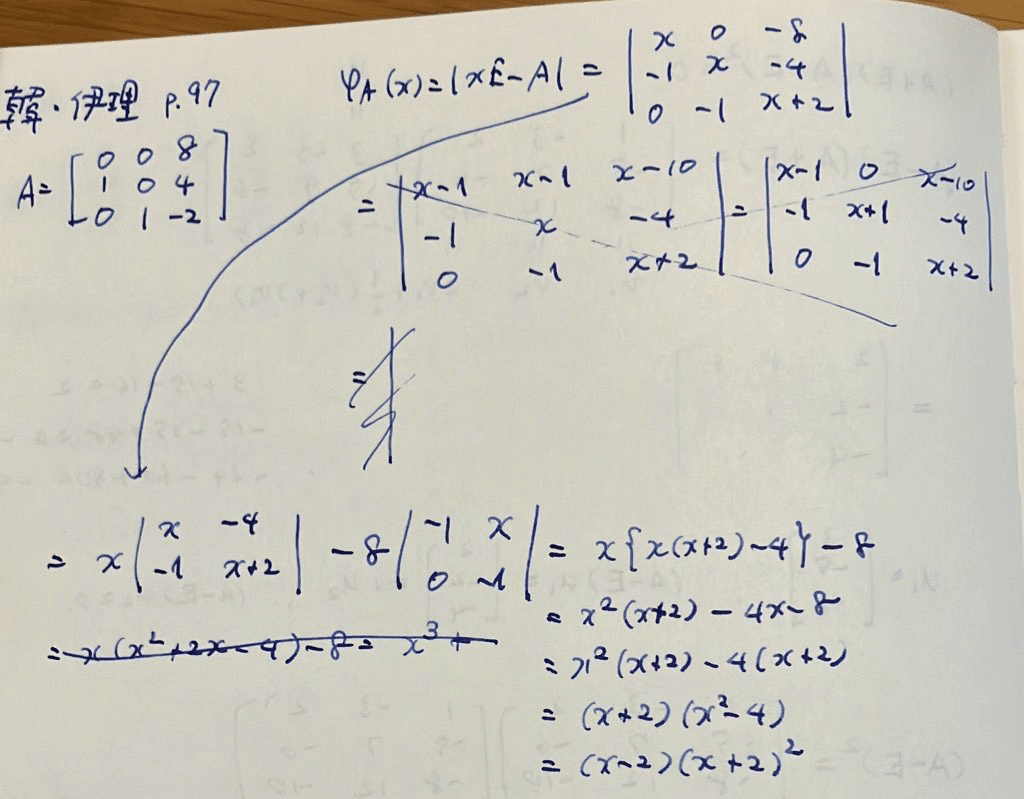
A+2Eのランクは2。これでジョルダン標準形と最小多項式は分かりました。
(A+2E)(A-2E)を計算すると、1列目が0でなく固有値-2の固有ベクトル。これをu_1とします。A-2Eの1列目をu_2とすれば、(A+2E)u_2=u_1です。
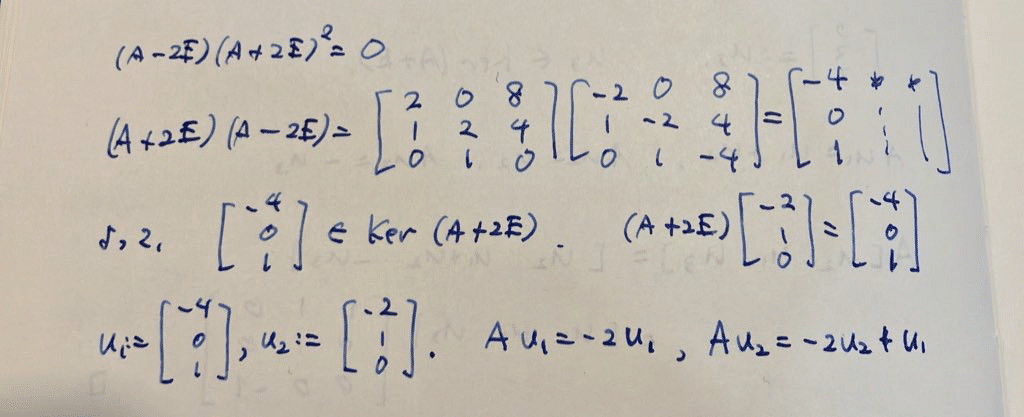
何か不安を感じたので、Au_2=-2u_2+u_1を確認しました。問題なし。
固有値2の固有ベクトルも見つけます。(A+2E)^2を計算すると1列目が0でないので、これが固有ベクトル。u_3とします。念のため検算。
[u_1 u_2 u_3]によってジョルダン標準形にできました。
（おしまい）
この記事が気に入ったらサポートをしてみませんか？