
ブール代数のスペクトル: 真理値表たちを開基とする直積空間!!
この記事はMath Advent Calender 2022の1日目の記事として作成しました。
内容のレベルは大学数学で、ジャンルは束論、位相空間論、少し圏論です。
全体的に『位相と論理』という教科書を参考にしています(末尾の参考文献1)。
0.はじめに
この記事では、「ブール代数のスペクトル」と呼ばれるものを定義することをゴールとします。そこへ至る過程で位相空間論のよい復習になり、学びがあると思ったのでテーマに選びました。
この内容は、私が去年か今年に『位相と論理』(文献1)という本を知り、その輪読会に参加して学んだことです。輪読会ではいろいろ教えていただきました。この場を借りて御礼申し上げます。
この本は束論・論理学・位相・圏論を扱っており、異なるジャンルが組み合わさっているのが面白かったです。
ブール代数のスペクトルを定義することは、本ではたった一行で書かれているので、記事にするほどのことではないかもしれませんが、私はその一行を理解するために結構いろいろ学びました。また、論理学の世界に位相空間論の道具を持ち込むための重要なポイントの一つだったと感じており、そのこともテーマに選んだ動機です。
1.目標
$${B}$$をブール代数とします。また、$${\mathbf{2}=\{0,1\}}$$もブール代数とします。
$${B}$$から$${\mathbf{2}}$$へのブール準同型(ブール代数間の束準同型)の全体を$${X}$$とします。すなわち、
$$
X:=\{x:B\to\mathbf{2}\mid xはブール準同型\}
$$
です。$${X}$$は直積$${\mathbf{2}^B}$$の部分集合と見ることもできます。
さらに、$${b\in B}$$に対して$${\phi(b):=\{x\in X\mid x(b)=1\}}$$とすると、
$${\{\phi(b)\mid b\in B\}}$$が$${X}$$の開集合の基になっていること
を示すのが本記事の目標です。これによって定まる位相空間をブール代数$${B}$$のスペクトルと呼ぶそうです。
位相については既知とします。ブール代数の定義を確認し、上記の舞台設定で積位相を考察することになります。
2.準備: ブール代数の定義
まずはブール代数の例を先に紹介します。
例2.1
集合$${X}$$の部分集合の全体(ベキ集合)$${P(X)}$$がブール代数の一例です。
そこでは、任意の$${A,B,C\in P(X)}$$に対して
和集合$${A\cup B}$$、
共通部分$${A\cap B}$$、
補集合$${X-A}$$
があり、さらに分配律
$${A\cap (B\cup C)=(A\cap B)\cup(A\cap C)}$$
が成り立ちます。そのようなものをブール代数といいます。
親しみ深いベキ集合がブール代数の典型例であるということを念頭に置き、一般的な説明のために、半束(はんそく)、束(そく)、分配束を定義していきます。
2.1 半束、束、分配束、ブール代数
定義2.2: 順序集合$${A}$$の部分集合$${S}$$が最小上界$${a}$$をもつとき、$${a}$$は$${S}$$のjoinであるといい、$${\lor S}$$と書く。
定義2.3: 順序集合$${A}$$の任意の有限部分集合がjoinをもつとき、$${A}$$はjoin半束であるという。
定義2.4: 順序集合$${A}$$の部分集合$${S}$$が最大下界$${b}$$をもつとき、$${b}$$は$${S}$$のmeetであるといい、$${\land S}$$と書く。
定義2.5: 順序集合$${A}$$の任意の有限部分集合がmeetをもつとき、$${A}$$はmeet半束であるという。
定義2.6: 順序集合$${A}$$において、任意の有限部分集合$${S}$$がjoinとmeetをもつとき、$${A}$$は束であるという。
いきなり定義がたくさん出てきて大変ですが、$${P(X)}$$に立ち戻って考えると分かりやすいと思います。$${P(X)}$$は包含関係によって順序集合とみなせます。$${P(X)}$$における$${\cup,\cap}$$が$${\lor,\land}$$に対応します。ただし、2個の元からなる部分集合$${\{a,b\}}$$に対しては、$${\lor \{a,b\}=a\lor b,\ \land \{a,b\}=a\land b}$$と書きます。3個以上の有限個についても同様です。
束においては、空集合$${\empty}$$に対し、$${\lor \empty}$$は束の最小元、$${\land \empty}$$は束の最大元、です。束の最小元を$${0}$$、最大元を$${1}$$と書きます。すなわち、$${\lor \empty=0}$$、$${\land \empty=1}$$です。
$${P(X)}$$では空集合$${\empty}$$が最小元であり、$${X}$$が最大元です。
問2.7: 一般の束において、$${\lor \empty}$$が最小元、$${\land \empty}$$が最大元になることを説明してみてください。
答: 空集合$${\empty}$$に対しては束の任意の元が上界となります。したがって空集合のjoinは束の最小元です。meetも同様です。
(論理式で書くともっと良さそう。私は無理)
束$${A}$$における分配律は
$$
a\land (b\lor c)=(a\land b)\lor(a\land c) ({a,b,c\in A})
$$
です。
定義2.8: 分配律が成り立つ束を分配束という。
ベキ集合での補集合に対応する概念も定義します。
定義2.9: 束$${A}$$、$${a\in A}$$に対して、
$$
a\land x=0、a\lor x=1
$$
となる元$${x\in A}$$が存在すれば、それを$${a}$$の補元という。
$${P(X)}$$では$${0}$$は$${\empty}$$、$${1}$$は$${X}$$に対応することを考えれば、補元が補集合に対応することが分かると思います。
実は、分配束では補元は存在すれば一意的であることが示せます。
問2.10: これを示してみてください。
答: $${x,y}$$がともに$${a}$$の補元であるとすると、
$${x=x\land 1=x\land (a\lor y)=(x\land a)\lor (x\land y)=0\lor (x\land y)=x\land y}$$
よって$${x\le y}$$。逆の不等号も同様に示せるので、$${x=y}$$。
そこで$${a}$$の補元があるなら、それを$${\lnot a}$$と書くことにします。
定義2.11: すべての元が補元をもつ分配束をブール代数という。
2.2 ブール代数の例
ブール代数の定義にたどり着きました。
ブール代数の例は、$${P(X)}$$の他に、次が挙げられます。
例2.12: 位相空間の開かつ閉である部分集合全体
例2.13: また、2元のみからなる集合$${\mathbf{2}=\{0,1\}}$$もブール代数とみなすことができます。
そこでは$${0\le 1}$$という順序であり、join、meet、補元は次のようになっています。
$${0\lor 1=1}$$、$${0\land 1=0}$$、$${\lnot 0=1}$$、$${\lnot 1=0}$$
以下のような真理値表がよく見られます。
$$
\begin{array}{c|c|c|c}\hline
p & q & p\lor q & p\land q\\ \hline
1 & 1 & 1 & 1 \\
1 & 0 & 1 & 0 \\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 \\ \hline
\end {array}
$$
$$
\begin{array}{c|c}\hline
p & \lnot p \\ \hline
1 & 0 \\
0 & 1 \\ \hline
\end{array}
$$
ブール代数$${\mathbf{2}}$$は上記のような真理値表で表されるわけです。
$${0}$$を$${\tt{false}}$$、$${1}$$を$${\tt{true}}$$と思うとよいです。
2.3 ブール準同型
ブール代数$${B}$$からブール代数$${B'}$$への写像$${f:B\to B'}$$が、$${B}$$の任意の有限部分集合のjoinとmeetを保つとき、ブール準同型と呼ぶことにします。
よって、$${f:B\to B'}$$がブール準同型ならば、任意の$${a,b\in B}$$に対して、
$$
f(a\lor b)=f(a)\lor f(b)
$$
$$
f(a\land b)=f(a)\land f(b)
$$
が成り立ちます。
このとき、$${f(\lnot a)=\lnot f(a)}$$も成り立つことが示せます。すなわち、ブール準同型は$${\lnot}$$も保つわけです。
問2.14: これを示してみてください。
答: $${b\in B}$$に対して$${f(\lnot b)\land f(b)=f(\lnot b \land b)=f(0)=0}$$
(なお$${f(0)=0}$$は$${f(\land \empty)=\land f(\empty)=\land\empty=0}$$より)
補元のもう一方の条件も満たすことが示せるので、$${f(\lnot b)}$$は$${f(b)}$$の補元である。
例2.15: ブール準同型$${B\to \mathbf{2}}$$
このようなブール準同型たちは、$${b_1,b_2\in B}$$に対して、以下のような真理値表を構成すると考えられます。
$$
\begin{array}{c|c|c|c}\hline
b_1 & b_2 & b_1\lor b_2 & b_1\land b_2\\ \hline
1 & 1 & 1 & 1 \\
1 & 0 & 1 & 0 \\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 \\ \hline
\end {array}
$$
$$
\begin{array}{c|c}\hline
b_i & \lnot b_i \\ \hline
1 & 0 \\
0 & 1 \\ \hline
\end{array}
\quad(i=1,2)
$$
この表ではたった2元$${b_1,b_2}$$だけに対して書きましたが、$${B}$$の任意の元に対して、このような真理値表が書けるとします。
そうすると、$${X=\{x:B\to\mathbf{2}\mid xはブール準同型\}}$$は、ブール代数$${B}$$において考えられる真理値表全部を集めた”でっかい真理値表”と思えてくるのですが、いかがでしょうか。
3.直積
3.1 写像と見るか、積と見るか
$${X=\{x:B\to\mathbf{2}\mid xはブール準同型\}}$$という集合が登場しました。これはブール準同型とは限らない写像全体である$${\{x:B\to\mathbf{2} \}}$$という集合の部分集合です。$${\{x:B\to\mathbf{2} \}}$$は$${\mathbf{2}^B}$$とも書かれます。
すなわち、
$$
X\subset\mathbf{2}^B=\{x:B\to\mathbf{2} \}
$$
です。
$${\mathbf{2}^B}$$は、$${B}$$の任意の元$${b}$$に対し、$${\mathbf{2}}$$の元である$${0}$$か$${1}$$を対応させる写像たちです。
これは別の見方をすれば、$${B}$$の元の分だけ箱があり、その箱の中には$${0}$$か$${1}$$が入っているようなもの、とも思えます。
$${\mathbf{2}^B}$$のことを直積と呼びます。
直積の他の例としては、$${xy}$$平面の点$${(x_1,y_1)}$$たちが考えられます。その点たちは、2個の箱にそれぞれ$${x_1}$$と$${y_1}$$という成分が入っており、それらを括弧の中に並べて書いたものと思えます。
$${\mathbf{2}^B}$$の場合は、$${B}$$の濃度の分だけある箱のそれぞれに$${0}$$か$${1}$$が入っているものであり、$${B}$$の濃度の分だけ$${\mathbf{2}}$$の積をとったものです。
つまり、$${\mathbf{2}^B}$$は、
①写像の集まり
②たくさんの箱の中に$${\mathbf{2}}$$の元が入っているもの
の両方の見方ができます。
直積らしく、次のように書くことができます。
$$
\mathbf{2}^B=\Pi_{b\in B}\mathbf{2}_b
$$
ただし、任意の$${b\in B}$$に対して$${\mathbf{2}_b=\mathbf{2}}$$
しかし、①のように$${f\in\Pi_{b\in B}\mathbf{2}_b(=\mathbf{2}^B)}$$はあくまで写像なので、$${b\in B}$$に対して$${f(b)\in\mathbf{2}_b=\mathbf{2}}$$と書けます。
(省略しましたが、本当は直積の定義では選択公理に言及する必要があります。普通に生きている人が初めて選択公理に出会うのは、直積の定義でだと思いますが、いかがでしょうか。)
3.2 位相を考える
さて、ここからは位相について考えます。
$${\mathbf{2}}$$には離散位相が入っているとします。
すなわち、$${\mathbf{2}}$$の開集合系は$${\{\empty,0,1,\mathbf{2}\}}$$です。
$${\mathbf{2}}$$はコンパクトです。なぜなら元が2個しかないので。
また、離散位相を入れたのでハウスドルフでもあります。
このとき、直積$${\mathbf{2}^B=\Pi_{b\in B}\mathbf{2}_b}$$に積位相という位相を入れることができます。次節でそのことについて説明していきたいと思います。
3.3 積位相
積位相の定義は「各射影を連続にする最弱の位相」です(より一般的には各射影たちから誘導される位相です)。
$${\mathbf{2}^B=\Pi_{b\in B}\mathbf{2}_b}$$の場合で言えば、射影とは、$${b\in B}$$に対して$${\pi_b:\mathbf{2}^B\to \mathbf{2}_b}$$という写像であり、$${f\in \mathbf{2}^B=\Pi_{b\in B}\mathbf{2}_b}$$に対して$${\pi_b(f)=f(b)\in \mathbf{2}_b=\mathbf{2}}$$を満たすものです。
この$${\pi_b}$$がすべての$${b\in B}$$について連続になる、そのような$${\mathbf{2}^B}$$の位相で最弱なものが積位相です。
最弱な位相ではなくても、たとえば$${\mathbf{2}^B}$$に離散位相を入れれば、各射影$${\pi_b}$$を連続にすることはできます。しかし、離散位相を入れるという要求は過大であり、純粋に直積をとることだけによる影響を考慮した、必要最小限の位相を考えることに意味があります。したがって最弱な位相をとります。
3.4 積の位相を最弱にすることの圏論的意義
積位相が最弱であるべきという要請は、圏論的にも説明できます。
ある圏$${\mathcal{C}}$$において、対象$${X_1,X_2}$$の積とは、対象$${P}$$で下記の可換図式を満たす射$${f}$$が一意的に存在するものでした。
すなわち、$${\mathcal{C}}$$の任意の対象$${A}$$と下図のような射$${f_i (i=1,2)}$$に対して、$${f_i=\pi_i\circ f (i=1,2)}$$を満たすものです。
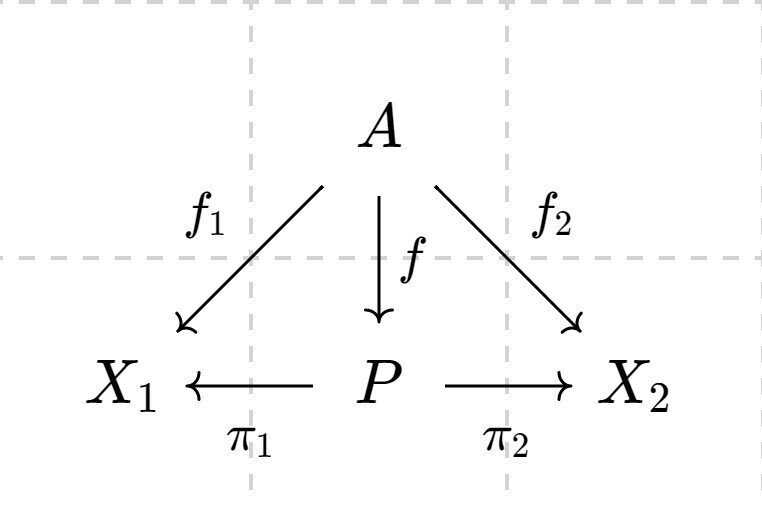
圏$${\mathcal{C}}$$が位相空間の圏$${\textbf{Top}}$$のとき、直積因子が2個の場合ではありますが、$${P=\Pi_{i=1,2}X_i}$$と射影$${\pi_i}$$が圏論的な積の定義と合致していることを見たいと思います。
直積$${P=\Pi_{i=1,2}X_i}$$には$${\pi_i}$$が連続になる最弱な位相を入れるので、確かにこれらは圏$${\textbf{Top}}$$の対象と射です。
そして、上図のような$${A}$$と$${f_i}$$があるとき、位相空間の圏なので、射$${f_i}$$は連続写像です。
このとき、$${f_i=\pi_i\circ f}$$が成り立つには$${a\in A}$$に対して$${f(a)=(f_1(a),f_2(a))}$$と定義するしかありません。
問題は、「この定義による$${f}$$が連続なのか」ということです。
ここで最弱の位相であることが効いてきます。
$${\mathcal{O}_i}$$を$${X_i}$$の開集合とすると、$${\pi_1^{-1}(\mathcal{O}_1)=\mathcal{O}_1\times X_2}$$です。
同様に、$${\pi_2^{-1}(\mathcal{O}_2)=X_1\times\mathcal{O}_2}$$です。
$${\pi_i}$$が連続であるということから、これらはどちらも$${P}$$の開集合です。
これらの共通部分
$${\pi_1^{-1}(\mathcal{O}_1)\cap\pi_2^{-1}(\mathcal{O}_2)}$$
$${=(\mathcal{O}_1\times X_2)\cap(X_1\times\mathcal{O}_2)}$$
$${=\mathcal{O}_1\times \mathcal{O}_2}$$
も$${P}$$の開集合です。
そして、$${\mathcal{O}_1\times \mathcal{O}_2}$$という形の集合の和集合として書けるもの、それも$${P}$$の開集合なのです。
結局、$${\mathcal{O}_1\times \mathcal{O}_2}$$の$${f}$$による逆像が$${A}$$で開集合になっていることを確認すれば$${f}$$の連続性が示せたことになります。それを示したのが次の式です。
$${f^{-1}(\mathcal{O}_1\times \mathcal{O}_2)}$$
$${=f^{-1}(\pi_1^{-1}(\mathcal{O}_1)\cap\pi_2^{-1}(\mathcal{O}_2))}$$
$${=f^{-1}(\pi_1^{-1}(\mathcal{O}_1))\cap f^{-1}(\pi_2^{-1}(\mathcal{O}_2))}$$
$${=(\pi_1\circ f)^{-1}(\mathcal{O}_1)\cap (\pi_2\circ f)^{-1}(\mathcal{O}_2)}$$
$${=f_1^{-1}(\mathcal{O}_1)\cap f_2^{-1}(\mathcal{O}_2)}$$ (*)
$${f_i}$$が連続であることから、(*)の形の部分集合は$${A}$$の開集合であることが分かります。
また、$${P=\Pi_{i=1,2}X_i}$$には射影たちが連続になる最弱の位相を入れていたので、$${\mathcal{O}_1\times \mathcal{O}_2}$$の形の集合の逆像についてのみ、開であることを見ればよかったのです。
もし、最弱ではない位相を入れていると、それら以外の逆像も開であることを示さなければいけませんが、それを成り立たせる条件がなく、行き詰まってしまいます。
今はたった2個の直積因子だったのですが、無限個の直積因子がある場合に直積に離散位相を入れてしまうと、無限個の$${\pi_i^{-1}(\mathcal{O}_i)}$$という集合たちの共通部分も直積集合で開となり、その$${f}$$による逆像も開とならなければいけません。
それは、$${f_i^{-1}(\mathcal{O}_i)}$$という形の集合の無限個の共通部分が開であることを示さなければならなくなり、個々の$${f_i^{-1}(\mathcal{O}_i)}$$は開ですが、無限個の共通部分が開になることは位相の定義で保証されておらず、結局、$${f}$$の連続性が示せない、ということになります。
したがって、圏論的に見ても積に最弱の位相を入れることは重要だったわけです。
また、確かに終域の位相が弱いと、そこへの写像は連続になりやすいという感覚があります。
3.5 開集合の具体的な形
では$${\mathbf{2}^B=\Pi_{b\in B}\mathbf{2}_b}$$に入っている開集合の具体的な形を見ておきます。
各射影$${\pi_b}$$が連続になる最弱の位相である、ということから、
$${\mathbf{2}_b=\mathbf{2}}$$における開集合の$${\pi_b}$$による逆像は、$${\mathbf{2}^B=\Pi_{b\in B}\mathbf{2}_b}$$の開集合です。
$${\mathbf{2}_b=\mathbf{2}}$$における開集合は、$${\{\empty,0,1,\mathbf{2}\}}$$でした。
$${\pi_b^{-1}(\empty)=\empty}$$、$${\pi_b^{-1}(\mathbf{2})=\mathbf{2}^B}$$です。
また、
$${\pi_{b_0}^{-1}(1)=\Pi_{b\in B}P_b}$$
ただし、$${P_b=\left\{\begin{array}{cc}\{1\} & (b=b_0)\\ \mathbf{2} & (b\neq b_0) \end{array} \right.}$$
です。
すなわち、$${b_0}$$に対する直積因子だけは$${\{1\}}$$で、他の直積因子は$${\mathbf{2}}$$であるものです。$${0}$$に対する逆像も同様です。
これらが開集合となり、さらにそのような有限個の集合の共通部分も開集合でなければならないことから、$${\mathbf{2}^B=\Pi_{b\in B}\mathbf{2}_b}$$の開集合の基は、有限個の直積因子は$${\{0\}}$$か$${\{1\}}$$で、その他の直積因子は$${\mathbf{2}}$$であるもの、ということになります。
$${\mathbf{2}^B=\Pi_{b\in B}\mathbf{2}_b}$$の任意の開集合は、それらの和集合で書けます。
4.ゴール
$${\phi(b)=\{x\in X\mid x(b)=1\}}$$が開集合の基になっていることを見ます。
$${X\subset \mathbf{2}^B}$$でした。
$${X}$$には相対位相が入っています。
$${\phi(b)=\{x\in X\mid x(b)=1\}=\pi_b^{-1}(1)\cap X}$$です。
これは、$${\mathbf{2}^B}$$の開集合の基と$${X}$$の共通部分という形ですので、$${X}$$の開集合の基です。
以上で目標としていたことを確認することができました。
5.補足
このような位相の基によって生成される位相空間をブール代数$${B}$$のスペクトルと呼ぶそうです。『位相と論理』では、このことを用いてスペクトルがStone空間というものであることを示し、Stoneの双対定理に繋がっていきます。
本によると、これらは1930年代にStoneさんによって示されていたそうです。
ブール代数のスペクトルは、可換環でいえば素イデアルの空間だということですが、その対応は私はまだ勉強しておらずよく分かりません。
6.まとめ
束論を復習してブール代数の定義を確認しました。
ブール準同型$${B\to \mathbf{2}}$$はでっかい真理値表のようだと私は思っています。
積位相が最弱であるべきことをしつこく見ました。
$${\phi(b)=\{x\in X\mid x(b)=1\}}$$が開集合の基になっていることを確かめ、晴れてブール代数のスペクトルを定義できました。
7.参考文献
I.M. シンガー・J.A. ソープ 著、赤攝也 監訳、松江広文・一楽重雄 訳『トポロジーと幾何学入門』(培風館、1976年)
