
【高校数学】私が直線の方程式ax+by+c=0を苦手なのを克服する話
私はax+by+c=0が苦手である
中学校や高校の数学で直線の方程式$${y=ax+b}$$を習いました.
$${a}$$が傾きで$${b}$$が$${y}$$切片で,というふうにすぐグラフが描けます.
例えば$${y=2x+3}$$という式を与えられたら,頭の中にすぐに次のようなグラフを思い浮かべることができます.

ところが,高校の数学でときどき出てくる$${ax+by+c=0}$$という形式は,見ると思考停止してしまいます.私はそれがどんな直線かすぐには想像できません.
なので,いつも仕方なく,$${b\neq0}$$なら移項して$${y=-\frac{a}{b}x-\frac{c}{b}}$$の形に直してからグラフを描きます.
しかし,移項して割ると分数になるかも知れずごちゃごちゃしているし,面倒くさいし,もういい大人になったので,いい加減$${ax+by+c=0}$$を克服しようと思います.
今回の目的は,$${ax+by+c=0}$$という式を眺めただけで,だいたいどういう直線かが分かるようになること,です.
それは垂直なベクトルで表される
結論を言ってしまうと,$${ax+by+c}$$のグラフは次のベクトルと垂直な直線を平行移動したもののようです.
$$
\begin{bmatrix}a\\ b \end{bmatrix}
$$
これは$${x}$$座標成分が$${a}$$で,$${y}$$座標成分が$${b}$$である2次元ベクトルです.
この「あるベクトルに垂直な直線を平行移動したもの」ということを見ていきたいと思います.
まずはax+by=0の場合
簡単な場合として$${c=0}$$のとき,すなわち$${ax+by=0}$$のときを考えてみます.
これはベクトルの内積を使うと,次のように書き換えることができます.
$$
ax+by=\begin{bmatrix}a\\ b \end{bmatrix}\cdot\begin{bmatrix}x\\ y \end{bmatrix}=0
$$
いまは$${{a\brack b} \neq 0}$$としておけば,$${a\brack b}$$との内積が0である$${x\brack y}$$というのは,原点を通り$${a\brack b}$$と垂直な直線の式を表します.
たとえば,$${2x+3y=0}$$の場合は
$$
2x+3y=\begin{bmatrix}2\\ 3 \end{bmatrix}\cdot\begin{bmatrix}x\\ y \end{bmatrix}=0
$$
と書けるので,原点を通りベクトル$${2\brack 3}$$と垂直な直線を表します.
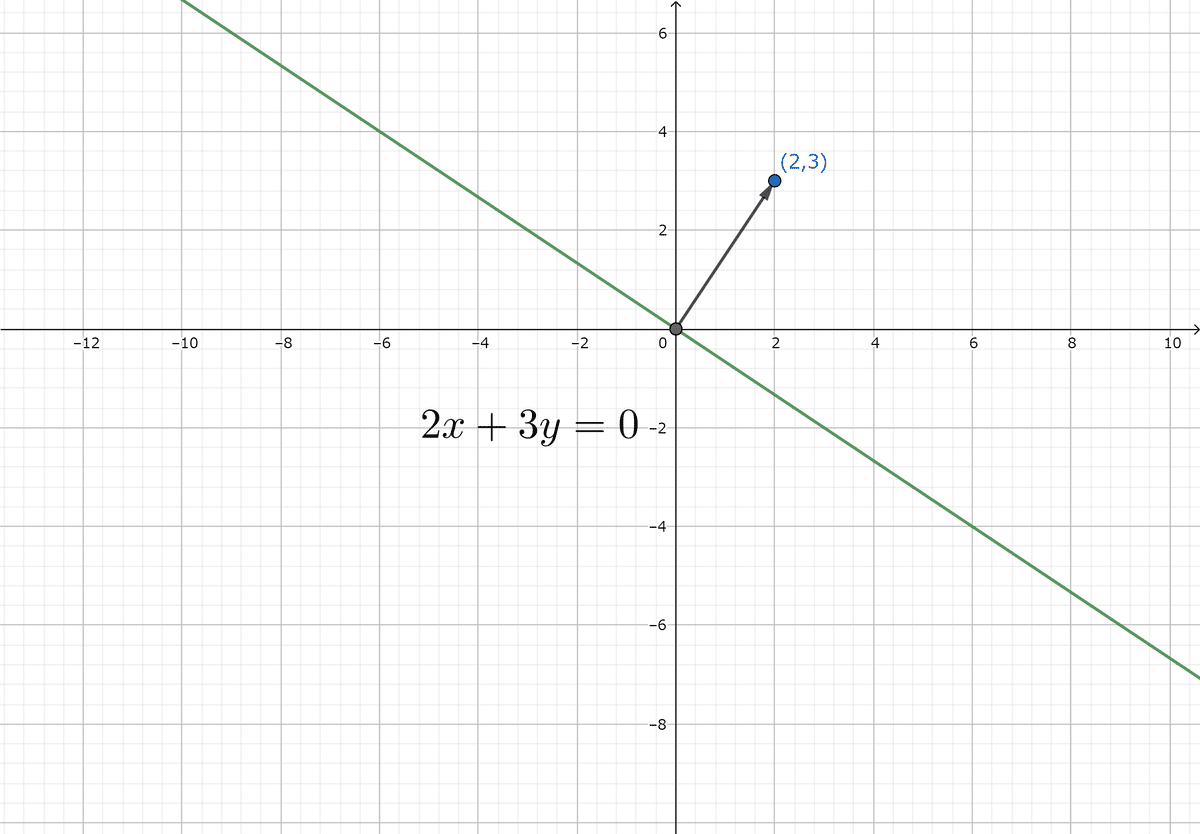
上のグラフのように,$${2\brack 3}$$は第1象限を向いているベクトルであるから,それに垂直な直線は右肩下がりとなります.
逆に,たとえば$${2\brack -3}$$のような第4象限を向いているベクトルによって表される直線$${2x-3y=0}$$は右肩上がりのグラフとなります.

ax+by+c=0の場合
では一般の場合として$${c=0}$$とは限らないとき,すなわち$${ax+by+c=0}$$のときを考えてみます.
これはさきほどの$${ax+by=0}$$で表される原点を通る直線を,適当に平行移動したものであることが分かります.
どの方向に平行移動するのか,ということは次の式変形を見れば分かります.
$$
ax+by+c=0 \Longleftrightarrow {a\brack b}\cdot{x\brack y}=-c
$$
ここで,
内積と$${c}$$は符号が反対である.
内積がプラスなら$${x\brack y}$$は$${a\brack b}$$と同じ側を向く(なす角が90°より小さい).
内積がマイナスなら$${x\brack y}$$は$${a\brack b}$$と反対側を向く(なす角が90°より大きい).
したがって,$${c>0}$$ならば直線のグラフは$${a\brack b}$$と反対の象限,$${c<0}$$ならば同じ象限を通っていることが分かります.直線$${ax+by+c=0}$$のグラフは$${a,b,c}$$の符号に応じて次の図のような配置となります.ただし,$${a}$$はたいていプラスでとるのでプラスのみとしました.

これで当初の目的であった$${ax+by+c=0}$$という式を眺めただけで,だいたいどういう直線かが分かるようになったと思います.
ちなみに,$${a\neq0,b\neq0,c\neq0}$$ならば,$${ax+by+c=0}$$を変形して
$$
\frac{x}{(\frac{c}{a})}+\frac{y}{(\frac{c}{b})}+1=0
$$
とすれば,あまり綺麗な形ではなく趣旨から外れますが,$${x}$$切片が$${-\frac{c}{a}}$$,$${y}$$切片が$${-\frac{c}{b}}$$であることは一瞬で読み取れます.

応用:円の接線
円$${x^2+y^2=r^2}$$上の点$${x_0,y_0}$$を通る接線の方程式は次です.
$$
x_0x+y_0y=r^2
$$
私は高校生の頃,この公式の意味はよく理解していませんでした.しかし,$${ax+by+c=0}$$のグラフについて学んだ今なら,上記の式の意味は明白です.
つまり,円上の点$${x_0,y_0}$$における接線は,ベクトル$${x_0\brack y_0}$$に垂直な直線であるから,$${x_0x+y_0y+c=0}$$という形です.
そして,点$${x_0,y_0}$$が円上の点であることから$${c=-r^2}$$であることが即分かります.

次回予告:点と直線の距離をあえて3次元で考えてみる
今回は$${ax+by+c=0}$$という式を,2次元ベクトルの内積の式
$$
{a\brack b}\cdot{x\brack y}=-c
$$
に変形して考えてみました.
次回は,別の視点として,3次元でのベクトルの内積
$$
ax+by+c=\begin{bmatrix}a\\ b\\c\end{bmatrix}\cdot\begin{bmatrix}x\\ y\\1\end{bmatrix}=0
$$
として考えてみたいと思います.それにより,点と直線の距離について図形的な理解ができると思われます(いささか強引ですが).
(サポートベクターマシンという機械学習アルゴリズムにも関連があるようです)
おわり
