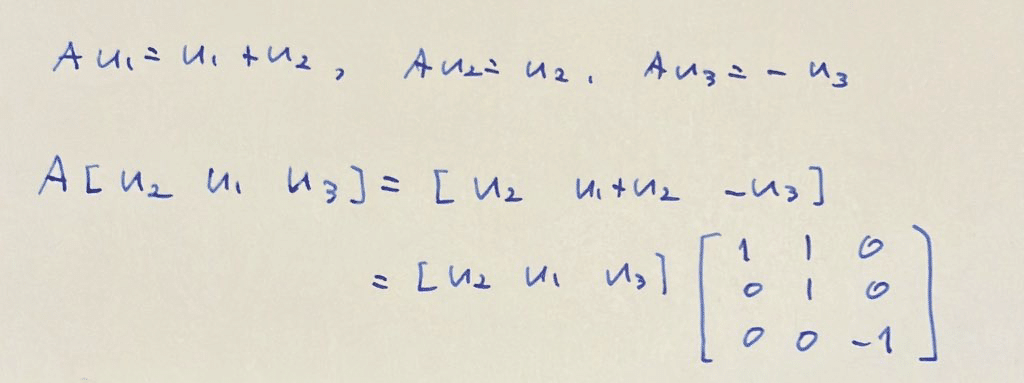西山先生のSGCのジョルダン標準形

今日も今日とてジョルダン標準形！
今日は西山享先生のSGCのp54の行列で！

今日の行列

今日の行列は固有多項式が難しい。愚直に計算しました。

固有多項式。今日のは難しい。

A-Eのランクは2。これでジョルダン標準形と最小多項式が分かりました。

A-Eのランクからジョルダン標準形と最小多項式が分かった

(A-E)(A+E)を計算したら1列目が0でないので、A+Eの1列目をu_1する。u_2:=(A-E)u_1とすればこれが固有値1の固有ベクトル。

u_1, u_2を見つけた

次に(A-E)^2の0でない列を探せば1列目がそう。それを4で割ったものをu_3とすればこれが固有値-1の固有ベクトル。

u_3も見つけた

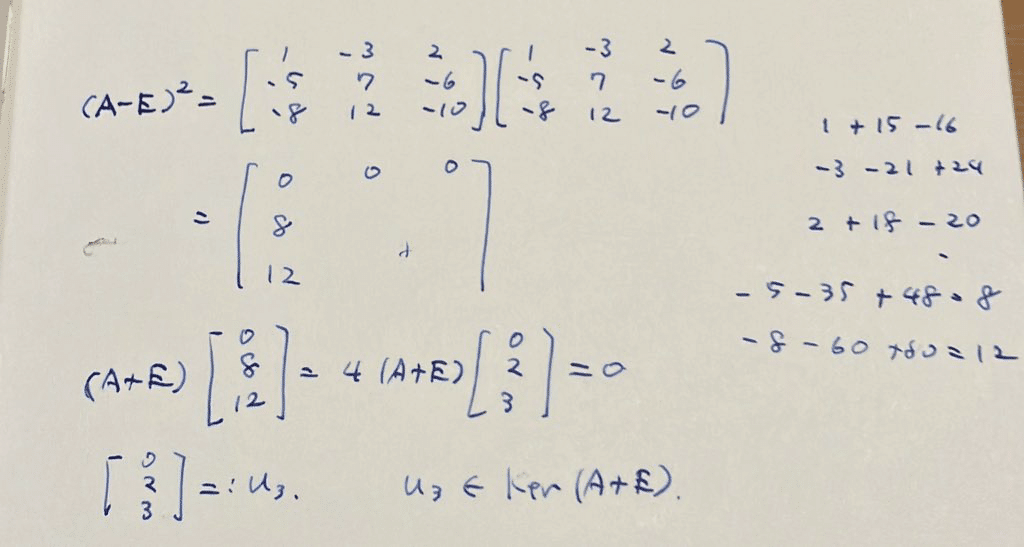
[u_2 u_1 u_3]と並べたらこれでAはジョルダン標準形にできる。
（u_1とu_2の添字の付け方は逆にすればよかったが後の祭り）

おしまい。

ジョルダン標準形にできた