
易占いは占いじゃない。
易は中国古来の占いで古典と思われていますがシンクロニシティを呼び覚まし、縁を紡ぐ、そんな占いです。心理学の権威カール・ユングも勉強した素晴らしい占いですが文献が少なくなってるのでやれる人は少ないです。貴重な文献は高値で取引されており入手困難だったりします。
易経は四書五経と呼ばれる当時の中国で1冊でもものにすれば食いはぐれないとされていました。占いが学問だったのです。
先程も述べたように近年ではカール・ユングがシンクロニシティという視点で読み解き解釈を増やしました。その後、科学的なアプローチもされていますが、"偶有性"を解き明かすことは難儀なことです。
科学的な思考で仕組みを読み解くとすればキーになるのは、カオス理論やバタフライ・エフェクトといったことを理解する必要があります。
カオス理論とは、ほんのわずかに初期条件が変わるだけで結果に大きな差が起こる現象や予想がつかないような複雑な現象を起こす微分方程式・力学系を扱う理論のことをさしています。
ちなみに、カオスは、英語で混沌、無秩序を意味しています。
無秩序の中の秩序(法則)を見出す理論と理解していただいたほうがわかりやすいかもしれません
カオス理論の具体的な現象の例としては、気象学者のローレンツ(Lorenz)の話題があります。ローレンツは大気の変動モデルを研究していました。
本来はナビエ・ストークス方程式※という非線形の偏微分方程式によって大気変動は説明されますが、それを単純化し、3成分の常微分方程式と変形させ、数値計算を行ってみたのです。
※ナビエ–ストークス方程式は、流体の運動を記述する2階非線型偏微分方程式であり、流体力学で用いられる。
(微分方程式・・・解析学において、微分方程式とは、未知関数とその導関数の関係式として書かれている関数方程式)
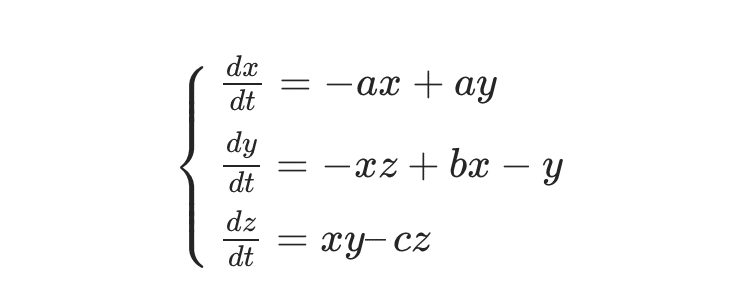
現実には細かい成分がありますが、例えば上図のx,y,zの3成分を、気温、湿度、風の強さと考え、気象現象を表すとみなすことができます。
ローレンツは、パラメータを
a=10、b=28、c=8/3
としたときに、実に複雑な気象現象が起こることを発見しました。
この結果は、「Deterministic Nonperiodic Flow(決定論的で非周期的な流れ)」という論文で発表されたそうです。

画像引用:Chaos7 Attracteurs étranges : L’effet papillon
上の画像に示されているように、あらゆる気象現象は、チョウチョの羽のような2つの輪っかへと引き込まれていきます。
一般に、力学系理論では、周囲の状態を引き寄せる集合のことを、アトラクター(attractor)と言います。
ローレンツの発見したアトラクターは、ローレンツ・アトラクター、またはストレンジ・アトラクターと呼ばれます。まさに奇妙なアトラクターです。
ローレンツは、その研究を講演で話す予定でしたが、会議の主催者が急いでいたため、勝手にそのタイトルをつけてしまったと言われています。
Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?”
(予測可能性:ブラジルの1匹の蝶の羽ばたきはテキサスで竜巻を引き起こすか?)
ちょっとしたチョウチョの羽ばたきが、地球の裏側で竜巻を引き起こすかもしれない。
これをバタフライ・エフェクトと一般に読んでいます。
参考:バタフライ効果 – Wikipedia
ローレンツはそこまでは言っていませんが、この表現は詩的で人気となったそうです。そのため、数学だけでなく一般に盛り上がっていく話題となりました。
その後、「人間は運命から逃れられるか?」という運命論と結び付けられ、多くのドラマや映画の題材となっています。
※今回参考にしたサイト(https://math-fun.net/20180712/519/#i-2)によれば「バタフライ・エフェクト」という映画や「STEINS;GATE(シュタインズゲート)」で扱われているとのこと。
(私も好きなシュタインズ・ゲートの世界観についてはまた別途説明が必要かと思いますので、次回以降のどこかで。)
"カオス"には、いくつかの定義があります。
その中で有名な定義が、初期状態に対する鋭敏性(sensitivity)。
多くの物理法則、微分方程式では、同じ初期状態が同じ結果を生み出すだけではなく、似ている初期状態は似ている結果を生み出すとされています。これは初期状態に関する連続性(continuity)と言われます。
ローレンツの方程式、カオス現象では、似ている初期状態から始まっても大きく異なる結果を生み出します。
ローレンツの方程式は、同じ初期状態が同じ結果をもたらす、決定論的なものです。
にもかかわらず、少し初期状態が違うだけで大きな違いを生み出してしまうものです。
例にあげた現実の気象現象にどこまでカオス現象が起こっているかは不明ですが、ローレンツの単純化した方程式ですら起こっていることが、より変数をたくさん持ち、これが現実に起こらないとは言えないでしょう。
説明が長くなりましたが、易が判断しているのはそういうカオス理論的な複雑なことであります。観測者たる占者は数学者である必要はなく、直感的に、むしろ現実に即した実践経験のある方がこの占いに好まれます。
カオス理論の参考はこちら様から
https://youtu.be/zUe1L8T8mms
カジュアルな占いの次元を超えたもの、という意味で易はもはや占いではないのです。
スピリチュアルと片ずけるのはもったいない事柄が沢山あります。現代科学でわからないものを全て不毛なものと扱う風潮はどうかと思います。
科学でもわからないものについてこそワクワクしませんか?
私は一学問を尊重しますが、一学問程度で世界を理解することは不可能であると思っています。多角的にみないと。
今回はそんな一例をだしてみました。
あなたの興味はどんな風に刺激されたでしょうか?
斑鳩入鹿
