
数学Ⅲ複素数「2章 複素数の極形式」・・・井出進学塾のマンツーマン授業の実況中継
こんにちは、井出進学塾(富士宮教材開発)です。
「1章 複素数平面」は、こちらです。
この講座で使っているワークシートは、こちらからダウンロードできます。
解説動画は埋め込みの他に、講座番号に再生時間を添えてリンクを貼っておきます。
リンクの方は別タグで開かれますので、使いやすい方でどうぞ。
1.複素数の極形式

第2章は、複素数のもう一つの表し方をみていきます。
「極形式」という、三角関数を利用した表し方です。
三角関数のからめることで、複素数平面の有用性が広がります。
とても不思議ですね。

第1講の続きです。複素数平面上のすべての点が、極形式で表されることを確認します。

複素数を極形式に直す練習の前に、軽く「ラジアン」について、おさらいしておきます。
ここから先は、ある程度、三角関数について入ってないと、さすがに苦しいですので、不安のある方はそちらも見直しておきましょう。
第4講
![]()
![]()
(例題⑴)複素数を極形式に直す練習です。
複素数平面をしっかり図示するのが第1歩です。
![]()
(例題⑵)図をしっかりかいて、絶対値と偏角をしっかり読みとりましょう。

(例題⑶)特徴的な複素数(ここでは純虚数)も、複素数平面をしっかりかくことで、簡単に確認できます。
第5講
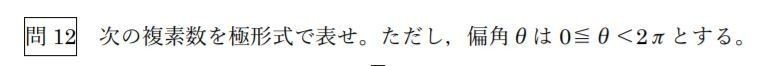

(問12⑴)それでは実際に極形式に直してみましょう。
必ず自分でやってみてから、動画解説をみるようにしましょう。

(問12⑵)絶対値を計算して求めました。こういう作業が必要な場合も、当然あります。

問12⑶ 与えられた複素数をa+biの形に変形する必要があります。

問12⑷ 偏角を求めるのに、少し戸惑うかもしれませんが、パターンが決まっているので、対応できるはずです。

問12⑸⑹ 軸上の点も、複素数平面の意味から、確実・正確に極形式に直しましょう。
2.積の極形式と商の極形式

極形式は、かけたりわったりすることで、その有用性が発揮されます。まずは、積の極形式の公式を導いておきましょう。

商の極形式の性質の証明です。
偏角についても、かけたときはたしたので、わったときはひく、というのは納得しやすいですね。

〔問13〕積と商の極形式の公式の使い方を確認します。

問14 極形式で表す練習です。
積・商の性質を上手に使いましょう。
3.複素数の乗法と回転

極形式の積と複素数平面上の図形の回転について確認します。
なぜ、そうなるかを、しっかり理解しておきましょう。

図形の回転について、簡単な問題で確認します。
複素数の極形式の有用性をつかみましょう。
以上です。ありがとうございました。
コメントなどいただけると、とてもうれしいです。
執筆:井出進学塾(富士宮教材開発) 代表 井出真歩
井出進学塾のホームページは こちらをクリック
無料体験授業、受付中です。
富士宮教材開発のホームページは こちらをクリック
各種教材を、そろえております。
ユーチューブチャンネルは こちら
