
数学Ⅲ「複素数平面」・・・井出進学塾のマンツーマン授業の実況中継
こんにちは、井出進学塾(富士宮教材開発)です。
今回は、数学Ⅲ「複素数平面」より、「第1章 複素数平面」を扱います。
この講座で使っているワークシートは、こちらからダウンロードできます。
解説動画は埋め込みの他に、講座番号に再生時間を添えてリンクを貼っておきます。
リンクの方は別タグで開かれますので、使いやすい方でどうぞ。
1.複素数の絶対値


数学Ⅱ段階で「複素数」は出てきましたが、それを座標平面上に表すことを考えます。
それが「複素数平面」です。
複素数平面に表すことによって、「複素数の絶対値(大きさ)」が定義されます。
第1講は、これらの用語の確認です。


問1問2に取り組みましょう。
図示や読み取りにより、複素数平面に慣れておきましょう。
また、複素数の絶対値の図形的な意味も確認しておきましょう。
2.共役な複素数とその性質

虚部の正負がちがうだけの2つの複素数、すなわち、a+bi と a-bi の2つの複素数のことを、「互いに共役(きょうやく)な複素数」といいます。
共役な複素数の性質は、さまざまなところで使える重要な性質です。
使いこなせるようになるため、一度、証明しておきましょう。
こういう手間をかけることが、数学の力をあげるために必要です。

〔共役な複素数とその性質①〕
共役な複素数という用語の確認と、和・差の性質の確認をします。
![]()
〔共役な複素数とその性質②〕
共役な複素数の性質の③、積の性質を証明します。
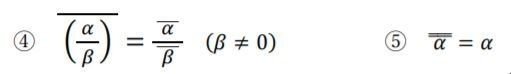
〔共役な複素数とその性質③〕
商の性質について証明します。先ほど証明した積の性質を上手に使いましょう。
3.実数であるための条件/純虚数であるための条件

複素数平面を使って、図形的にこれらの条件を理解しましょう。
ここは大切なところなので、必ず、よく理解しておきましょう。

問5.前講で確認した、「実数であるための条件」、「純虚数であるための条件」を使いこなすための練習問題です。
4.複素数の絶対値の性質
複素数の絶対値の性質を確認します。
①と②は、複素数平面を使って、図形的に解釈しましょう。

複素数の絶対値の性質③、④の証明に入る前に、「最重要公式」ともいうべき公式の確認です。

〔複素数に関する重要公式〕ベクトルの最重要公式と似たような重要公式が複素数にもあります。
これを使いこなせるようになるためにも、まず、しっかり証明しておきましょう。

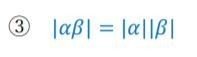
〔問6前半 複素数の絶対値の積の性質の証明〕
前講で証明した重要公式を使って証明します。重要公式はこのように使える、というよい例ですので、この証明はできるようにしておきましょう。

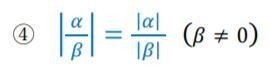
〔問6後半 複素数の絶対値の商の性質〕
前半で証明した積の性質を利用して証明します。
この証明法は、共役な複素数の性質の証明でも出てきた証明法です。
大切な考え方ということですね。

〔問7⑴ 積の形の複素数の絶対値の求め方〕
問6で証明した、絶対値の性質を利用する練習にしましょう。
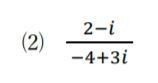
〔問7⑵ 商の形の複素数の絶対値の求め方〕
分母を実数化して計算しきれないこともありませんが、かなりたいへんで無理があります。複素数の絶対値の性質を利用しましょう。
5.最重要公式の利用
最重要公式を使う、スタンダード問題を、ここでいくつか紹介しておきます。

問8.「困った子は、Pちゃんと名前をつけて扱う。」というIOPが、生きてくる問題です。
「最」重要公式は、このように使います。
出し入れの感覚をつかみましょう。

これまで学習した内容の集大成のような問題です。
必ず完ぺきに理解し、いつでも解けるようにしておきましょう。
6.複素数の和と差の図示
複素数と図形の関係は「4章 図形と複素数」でじっくりみていきますが、ここでは、その導入として「和」と「差」を確認しておきましょう。

〔問10 複素数の和と差の図示〕
複素数と図形の関係は、4章でじっくり扱いますが、基本的な、和と差と複素数平面に現れる図の特徴について確認しておきましょう。
ベクトルのときと、同じような考え方をするので、ベクトルの理解にも助けになります。

問11.ひき算というのは、ひかれる数とひく数の関係はそのままに、ひく数を原点にひきよせる操作のことです。
こういう簡単な問題で、その感覚をつかみましょう。
7.補足
このシリーズをあげている最中にいただいた問題なので、解説動画でお応えしました。
以上です。ありがとうございました。
コメントなどいただけると、とてもうれしいです。
執筆:井出進学塾(富士宮教材開発) 代表 井出真歩
井出進学塾のホームページは こちらをクリック
無料体験授業も、受付中です。
富士宮教材開発のホームページは こちらをクリック
さまざまな教材を、準備しております。
ユーチューブチャンネルは こちら
