
「正多角形の作図」の実践、公開します!
こんにちは。ぐうぽんです。
先日、プログラミング教育の5年算数「正多角形の作図」を実践してきました。
過去に少人数算数での指導を行っていましたので、当時使っていた指導ノートとともに振り返ります。
こちらは、90%を無料にしている記事です。
最後だけ、有料にしています。
無料部分だけでも十分な内容に仕上げていますので、ぜひ最後までご一読いただけると嬉しいです。
プログラミング教育の手引が示す「正多角形の作図」
文部科学省「小学校プログラミング教育の手引」では、正多角形の作図について次のような目的を定めています。

ここで注目したいのは、”プログラミングを使えば人にとって難しい作図もコンピュータなら容易にできる”こと。
コンピュータは同じことを何百、何千、何万回も行えます。
ですので繰り返し処理を応用すれば、正多角形を書くことができます。
実施する授業の目標も、ここに帰結するよう促して指導しました。
1.算数で書き方を学ぶ
まず算数で本単元を進めます。
ですが
今の自分は家庭科なので、少人数算数担当の先生にもお声がけして、プログラミング実践当日にお手伝いをいただきました。
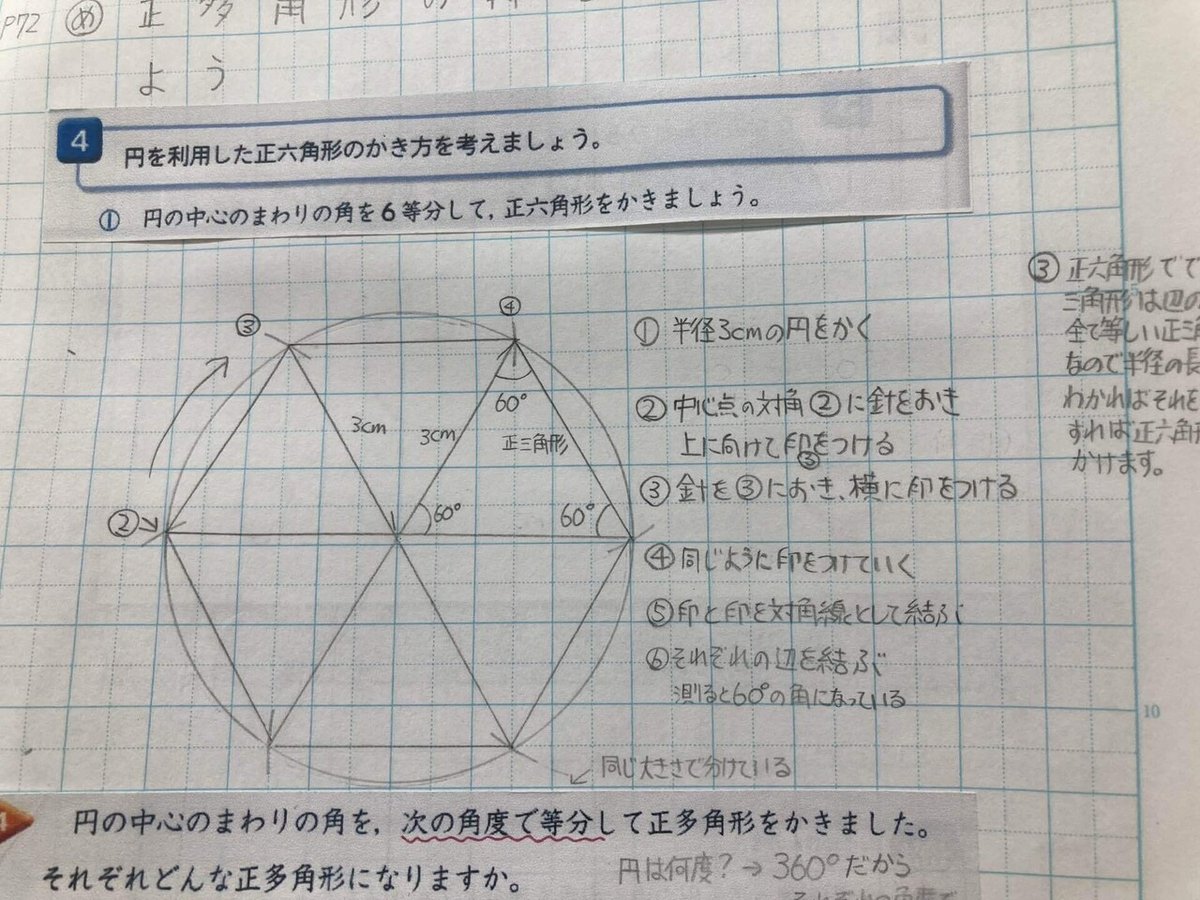
学習の流れは、正多角形の性質を理解→正多角形を書く→円と円周率の関係を理解となっており、授業では正五角形、正六角形の作図があります。
画像は指導当時使っていたノートです。
教科書では1辺の長さと角度を決めて書く方法と、円を使って等分する方法が示されています。

前者は始点がずれる、何度も角度を測るのでずれますし非効率的と分かります。

そのため後者のコンパスと分度器、定規を使って作図させ、その良さに気づかせます。
最後に、正多角形を書くときの条件を表でまとめ、一つの法則性を導き出します。
プログラミング的にはここがスタートで、法則性を利用して様々な正多角形を作図できることを理解させます。

正十角形くらいであれば手書きでも一見正確に書けるように見えますが、人間が行うと微妙なずれが起きますし、多角形の数が増えれば角度や辺も増え、結果的に書く手間も増えます。
そうした意味から、様々な正多角形の作図には、プログラミングを利用したほうが便利であると結論づけまさ。
2.学んだ知識技能でプログラミング
ここからプログラミングです。
導入として、まず先の算数で学んだ内容に触れ、正多角形を書くときの法則を思い出させます。
そして色々な正多角形をプログラミングを使って作図できる旨を伝え、学習目標として設定します。
活用したのは、みんなのコードが運営する「プログル」の多角形コースです。
こちらを推薦する理由は2つあります。
1つはチュートリアルに則ってプログラミングに必要な「順次」「反復」処理を理解できること。
もう1つはScratchよりも簡単かつ余計な操作で遊ばせない工夫があることです。
実際Scratchで実施したとき、作図でペンモードを追加する手間があったり、他のブロックで授業に関係のない操作で遊ぶ児童が続出したりと大変でした。
プログルはそういった手間も少なく、何よりプログラミングに不安をお持ちの先生でも簡単に使えると感じています。
手順に従ってロボットを動かすと、正三角形の作図でつまづきます。
「正三角形をかこうとして60 度(正六角形をかこうとして120 度)曲がると命令すると正しくかくことができないのはなぜか」、「なぜ正三角形のときは120 度で、正六角形のときは60 度でかけるのか」
でも私は何も言わず取り組ませます。
子どもたちが「あれ?」と思うことで、作図における疑問を児童同士で相談、試行錯誤するので、より作図の理解を深められると思います。
よろしければ、応援をお願いします! いただいたチップは、執筆やサポートの活動費に使わせていただきます
