
無限遠にある電荷がガウスの法則を取り戻す―リンドラー座標つれづれ(4)—
はじめに
しつこいが、リンドラー座標ネタは続く。本稿は、以下の記事の続きである。
問題をおさらいする。荷電粒子が$${z}$$軸上を相対論的な等加速度運動をしている状況を考える。$${t = -\infty}$$, $${z = +\infty}$$から原点に向かって移動してきて、$${t = 0}$$に$${z = b\,\,(>0)}$$に到達し、そこで折り返して$${t = +\infty}$$, $${z = +\infty}$$に向かって飛び去って行く。このとき、電荷が折り返し地点に来た時刻$${t = 0}$$に形成される電場は、下図のように、$${z = 0}$$において電気力線がプッツリと切れた形になってしまう。

式で書くと以下になる。この電場は$${z}$$軸のまわりに対称で、$${s}$$は動径方向の座標である。$${\theta(z)}$$は階段関数。
$${\displaystyle \bold E_A = \frac{qb^2}{\pi\varepsilon_0}\frac{(z^2-s^2-b^2)\hat{\bold z} + 2sz \hat{\bold s} }{ \left\{\sqrt{\left(z^2+s^2+b^2 \right)^2-\left(2zb \right)^2} \right\}^3 }\theta(z) }$$ 式1
ここで、$${z = 0}$$の境界をまたぐように閉曲面を設定して表面から出る電場を積分すると、閉曲面内部に電荷がないにも関わらず、積分値がゼロにならないため、一見ガウスの法則が破綻してしまう、という問題である。
この結果はもちろん誤りで、注意深く計算すれば、ガウスの法則はちゃんと成立するのだが、その仕組みはなかなか巧妙で、プロの理論物理学者でも間違えるほどである。この問題は、少なくも1950年代から認識されていたようだが、本質的な解決を見たのは2015年なので、割と最近の話なのだ。以下で、私の理解に基づいて解説する。
いざ、古典電磁気学のディープな世界へGo!
電場はどうなるべきなのか?
詳細な計算をする前に、電場がどのようになっていたらガウスの法則が回復するのかを考えてみよう。$${t = 0}$$の時点において、$${z < 0}$$の範囲は光円錐の外側なので、電場は生じようがない。図1で、切れた電場の力線を伸ばすとしたら、下図のように、$${z = 0}$$の境界面に沿って外側に伸ばすしかない。

このように、$${z = 0}$$の位置において、$${z}$$軸を中心に放射状に出る電場があると、ガウスの法則を成立させることができる。具体的な表式は、デルタ関数を用いて、
$${\displaystyle \bold E_\delta = \frac{q}{2\pi\varepsilon_0}\frac{s\hat{\bold s}}{s^2+b^2}\delta(z)}$$ 式2
となる。元の式1の電場にこれが付け加わるとガウスの法則が成立するのは簡単に確かめられる。というわけで、正解の電場の形は分かっているのだ。この問題の本質は、
この電場をいかに自然に導出するか?
元々の計算ではなぜこの電場を導出できないのか?
の2点に解答することにある。
以下、下記3つの論文に沿って解説する(いずれもネットでフリーで入手可)。(論文2の著者Jerrold Franklinは、論文1のJoel Franklinとは別人であることに注意。)
論文1:J. Franklin & D. J. Griffiths, 2014. The fields of a charged particle in hyperbolic motion. American Journal of Physics, 82(8): 755-763.
論文2:J. Franklin, 2014. Electric field of a point charge in truncated hyperbolic motion. arXiv: 1411.0640v3.
論文3:D. J. Cross, 2015. Completing the Lienard-Wiechert potentials: The origin of the delta function fields for a charged particle in hyperbolic motion. American Journal of Physics, 83(4): 349-352.
Franklin & Griffithsのアプローチ
この問題に対して、論文1のFranklinとGriffithsは、以下のようなアプローチをとっている。無限の過去から一様に加速するのではなく、今考えている等加速度運動を過去のある時刻$${t_0}$$で打ち切って、そこから先は等速運動だったと見なすのである(速度は連続になるように接続する)。これを、著者らは "truncated hyperbolic motion" と呼んでいる。"truncate"は「先の方を切り取る」というような意味らしいが、しっくりくる訳語がないので、以下ではそのまま使うことにする。このtruncatedな運動による電場を$${t_0}$$の関数として導出した後、$${t_0\to -\infty}$$の極限をとれば、無限過去から一様加速する場合と同じと言えそうである。
電場を計算する前に、無限過去から等加速度運動する場合と、truncatedな場合の本質的な違いを時空図で見てみよう(下図)。
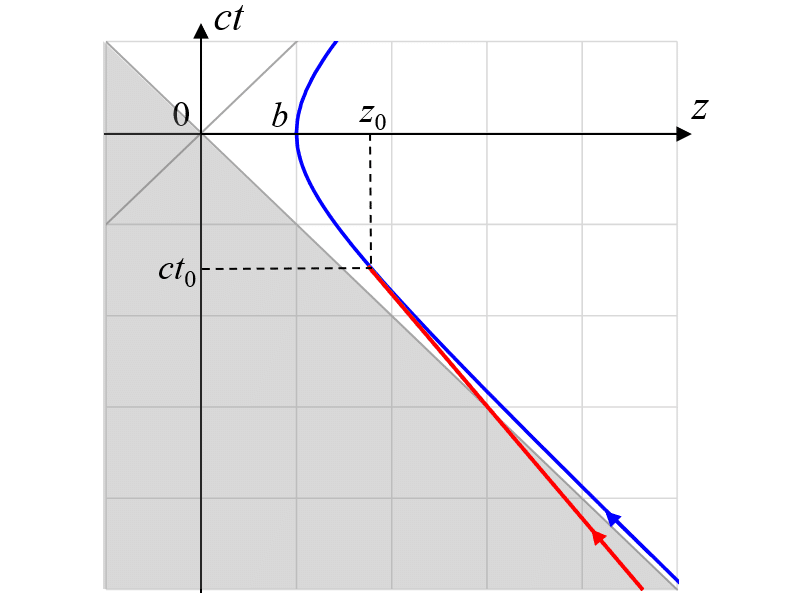
電荷の運動は、時刻t0以前は等速運動(赤線)、t0以降は一様加速(青線)に切り替わる。灰色に塗りつぶした領域は、一様加速(青線)の場合の、電荷の事象の地平面の外側を表す。
無限過去から等加速する場合(青線)、$${ct = -z}$$の直線が事象の地平面となるため、$${z = 0}$$にいる観測者は時刻$${t = 0}$$に突然電場を感じるようになるが、truncatedの場合(赤線)、この地平面がなくなる。$${z = 0}$$にいる観測者は、$${t < 0}$$の任意の時刻においても、電荷の等速運動起因の電場を感じることができる。この状況は、接続時刻$${t_0}$$を過去にずらしていっても変わらない。ただし、感じる電場の生成元である電荷の速度が光速度に近づいていく。
時空図ではなく、実空間で電場がどのようになるのか、定性的に見てみよう。
まず、予備知識として、等速直線運動する電荷が形成する電場は、下図のように、進行方向に対して縮んた形になる。

速度が光速に近づくと、前後方向に圧縮される。
この前後方向の圧縮度合は、速度が光速に近づくほど急激に大きくなり、特に、質量ゼロの荷電粒子が光速で動く場合、電場は完全に潰れてディスク状になる。この性質も、リエナール・ヴィーヘルトの遅延ポテンシャルから導出されるのだが、等速運動の場合、電場はあくまで前後に縮むだけで、放射状に広がる電場の中心は、その時刻における電荷の位置そのものである(遅延時刻ではない!)。
これを踏まえて、電荷が折り返し地点に向かっていくときの電場を図示すると、以下のようになる。等速運動と等加速度運動の接続位置を$${z_0}$$とする。$${z > z_0}$$のときは、まだ等速運動の電場のみ存在する(下図)。

接続点$${z_0}$$を過ぎると、$${z_0}$$を中心に、等加速度運動の電場が円形に広がっていく(下図)。

等加速度運動による電場(水色)が広がり始める
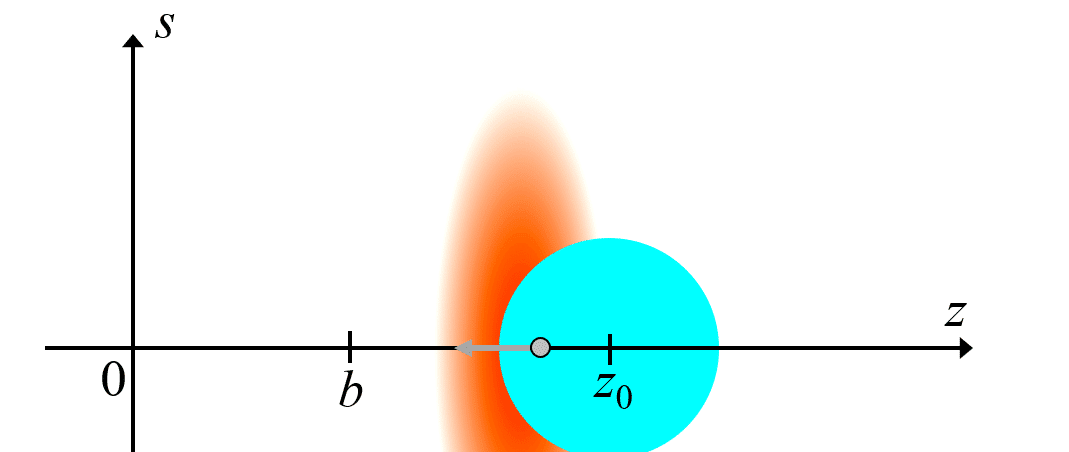
電荷の速度は当然光速よりも遅いので、電荷は境界円の内部にある。このとき、境界円の外側では、元の等速運動起源の電場がそのまま最初の速度を維持したまま前方に進み続ける。なので、等速度場の中心は、仮に電荷が等速運動を続けた場合にその時刻に来るであろう位置、となる。この辺が奇妙に感じるが、境界円の外側では、電荷が等加速度運動に転じたという情報を知りえないので、必然的にこうなる。
やがて電荷は減速していき、$${t = 0}$$で$${z = b}$$の位置に到達する(このとき速度ゼロ)。境界円の端の$${z}$$座標を$${z_A}$$, 等速度場の中心を$${z_V}$$とすると、$${0 < z_A < z_V< b}$$の順に並ぶ(下図)。

さてここで、接続点$${z_0}$$を遠方にずらしていくとどうなるか?$${z_0}$$が大きくなるほど($${t_0}$$が過去にシフトするほど)、$${z_0}$$を中心とする境界円の半径は大きくなり、端点$${z_A}$$はゼロに近づいていく。また、等速度場の方は、接続点が遠方にずれるほど、初速度が光速に近づいていくので、電場が前後方向にさらに潰れていく。また、$${z_V}$$の位置も、$${z_A}$$に近接していく(下図)。

このまま、$${t_0 \to -\infty}$$ ($${z_0 \to \infty}$$) の極限をとると、等速度場は$${z = 0}$$において厚さゼロのディスク状に放射する形になり、それに、等加速度場が接続する形になる、というのは想像つく。
そこで、論文1のFranklin & Griffithsは、この極限をとったときの電場を、光速で等速直線運動する電荷が作る電場
$${\displaystyle \bold E_\delta' = \frac{q}{2\pi\varepsilon_0}\frac{\hat{\bold s}}{s}\delta(z)}$$ 式3
と、等加速度運動による電場(式1)の和で書けると想定した(式3の導出はジャクソンの教科書に載っているらしいが、ガウスの法則を考えれば、この表式になることは分かる)。ところが惜しいことに、式3は、あるべき電場である式2と微妙に合わないのである(従ってガウスの法則も回復しない)。しかし、デルタ関数$${\delta(z)}$$は狙い通り出てきたので、基本路線は合ってそうな雰囲気である。
Jerrold Franklinによる修正
Franklin & Griffithsが、上記のtruncatedな運動を提示した論文1を出した後、Jerrold Franklinがすかさず論文2を出し、彼らの電場の計算に間違いがあることを指摘している(別人のFranklinがいてややこしいので、後者は以下Jerrold)。論文1では、$${t_0\to -\infty}$$の極限をとると、式3の電場が付加されるだろうと想定したが、この部分に飛躍があったのだ。論文1では、$${t_0\to -\infty}$$の極限をとる前の等速度場の表式を求めていないが、Jerroldはそれを具体的に計算し、以下の表式を示している(記号と単位系はこの記事に合わせた)。
$${\displaystyle \bold E_V = \frac{q}{4\pi\varepsilon_0}\frac{b^2\left\{ sz_0\hat{\bold s}+\left(zz_0-b^2 \right)\hat{\bold z} \right\}}{\left\{\sqrt{s^2b^2+\left(zz_0-b^2\right)^2} \right\}^3}}$$ 式4
この式の導出は私も確認できた。Jerroldは、この式に基づいて実空間における電場の力線を計算している。結果、図5-8で示した等速場と等加速度場の境界円において力線は折れ曲がるが、連続性は保たれることも示した(論文1では力線が不連続になる様子を図示していたので、これも間違い)。
さて、論文2の真骨頂は、式4で$${z_0\to\infty}$$(すなわち$${t_0\to-\infty}$$)の極限をとるところにある。式4の電場の$${z}$$成分は、この極限で明らかにゼロになる。一方、動径方向$${s}$$成分は、
$${\displaystyle E_{V\rho} = \frac{q}{4\pi\varepsilon_0}\frac{b^2sz_0}{\left\{\sqrt{s^2b^2+\left(zz_0-b^2\right)^2} \right\}^3} \\ \, \\ \quad \quad \to \left\{ \begin{array}{cl} \infty & (z = 0) \\ 0 & (z \ne 0) \end{array} \right.}$$ 式5
となるので、適当な係数$${K}$$を用いて、
$${\displaystyle \lim_{z_0\to\infty} E_{V\rho} = K\delta(z)}$$ 式5
と表してみる。この$${K}$$を求めるには、
$${\displaystyle K = \lim_{z_0\to\infty} \int_{-\infty}^\infty E_{V\rho}\,dz}$$ 式6
とすれば良さそうだが、これを計算すると、結局式3を再現してしまう。ここで気を付けなくてはいけないのは、上式の積分の範囲である。積分する電場$${E_{V\rho}}$$は等速場であるから、積分の上限は$${z\to\infty}$$ではなく、等加速度場との境界まで、となる(下図)。

従って、積分の上限は、
$${\displaystyle z_{\text{max}}=z_0-\sqrt{(ct_0)^2-s^2} \\ \, \\ \quad \quad = z_0 - \sqrt{z_0^2-b^2-s^2} \\ \, \\ \quad \quad = z_0 - z_0\sqrt{1 - \frac{s^2+b^2}{z_0^2}}}$$ 式7
となる。さらに、$${z_0\to\infty}$$の極限では、
$${\displaystyle \lim_{z\to\infty} z_{\text{max}} \simeq z_0 - z_0\left(1-\frac{s^2+b^2}{2z_0^2} \right) \\ \, \\ \quad \quad = \frac{s^2+b^2}{2z_0}}$$ 式8
と近似することができる。従って、デルタ関数の係数は、
$${\displaystyle K = \lim_{z_0\to\infty} \int_{-\infty}^{(s^2+b^2)/2z_0} E_{V\rho}\,dz \\ \, \\ \quad \quad = \frac{q}{2\pi\varepsilon_0}\frac{s}{s^2+b^2}}$$ 式9
となった(計算すると確かにこうなる)。これより、電荷が無限遠にあるときの等速場は、
$${\displaystyle \bold E_V = \frac{q}{2\pi\varepsilon_0}\frac{s\hat{\bold s}}{s^2+b^2}\delta(z)}$$ 式10
となり、求めるべき電場であった式2を導出できた。Jerroldさん、お見事!
Crossによる議論
上記の通り、truncatedな運動で考えて注意深く計算すれば、ガウスの法則を満たす電場を導出できたのだが、それでもまだ疑問が残る。ではなぜ、truncatedにしない(等速運動を接続しない)純粋な等加速度運動で考えた場合には、式2のデルタ関数が出てこないのでしょう?いずれの場合でも、議論の出発点は、点電荷のリエナール・ヴィーヘルトポテンシャルであり、共通ではなかったか。ここが、この問題の奥が深い所である。この部分の本質に迫り、計算方法により結果が変わる要因を解明したのが、Crossによる論文3である。非常にややこしい話で、一言で説明できる話ではないので、論文の筋書きに沿って解説する。式変形の詳細は省略する(一応、重要な部分はちゃんと追えた)。
リエナール・ヴィーヘルトポテンシャルの導出法はいろいろあるが、Crossは、グリーン関数を用いる正攻法を示している。電荷がある軌道を動いているとき、遅延時刻$${t'}$$における電荷の位置を$${\bold r'}$$で表し、その位置から現時刻の観測点$${\bold r(t)}$$まで伸ばしたベクトルを$${\bold r_n \equiv \bold r-\bold r'}$$とする(下図)。

電荷の軌道を$${\xi(t)}$$で表すと、観測点におけるスカラーポテンシャルとベクトルポテンシャルはそれぞれ、
$${\displaystyle V = \frac{qc}{4\pi\varepsilon_0}\int G\delta\left[\bold r'-\xi(t') \right]d\bold r'dt'}$$ 式11
$${\displaystyle \bold A = \frac{q}{4\pi\varepsilon_0c}\int G\bold v\delta\left[\bold r'-\xi(t') \right]d\bold r'dt'}$$ 式12
と書ける。ここで、$${G}$$はグリーン関数で、
$${\displaystyle G = \frac{\delta\left(ct - ct' - r_n \right)}{r_n}\theta(t-t')}$$ 式13
で与えられる。式11, 12の右辺を空間座標について積分すると、
$${\displaystyle V = \frac{qc}{4\pi\varepsilon_0}\int G\,dt'}$$ 式14
$${\displaystyle \bold A = \frac{q}{4\pi\varepsilon_0c}\int G\bold v\,dt'}$$ 式15
となる。ここで、右辺の$${G}$$の中の$${\bold r_n}$$は$${\bold r_n = \bold r - \xi(t')}$$ である。さらに、右辺の積分を実行すると、通常のリエナール・ヴィーヘルトポテンシャル
$${\displaystyle V = \frac{qc}{4\pi\varepsilon_0}\left[\frac{1}{cr_n-\bold r_n\cdot\bold v}\right]_{t_r}}$$ 式15
$${\displaystyle \bold A = \frac{\bold v}{c^2}V}$$ 式16
が得られる。ここで、$${t_r}$$は遅延時刻で、$${t - t_r = r_n(t_r)/c}$$の解である。式1の電場は、これらを用いて、$${\bold E = -\nabla V - \partial\bold A/\partial t}$$を計算して得たものである(計算は大変だが)。
このように、通常の遅延ポテンシャルをそのまま用いると、今の問題の解決にはならない。ここでCrossは、微分と積分の順序を入れ替えるという奇策に出る。電場を計算するには、$${\nabla V}$$を計算する必要があるが、この微分演算子を、式14の積分の中に入れてしまうのだ。
$${\displaystyle \nabla V = \frac{qc}{4\pi\varepsilon_0}\int \nabla G \,dt'}$$ 式17
途中を省略するが、右辺の積分を計算すると、
$${\displaystyle \int \nabla G \,dt' = \left[\frac{G\bold r_n}{c^2(t-t')-\bold v\cdot \bold r_n} \right]^\infty_{-\infty} \\ \, \\ \quad\quad\quad\quad\quad -\int G\frac{d}{dt'}\frac{\bold r_n}{c^2(t - t')-\bold v\cdot\bold r_n}dt'}$$ 式18
という形になる。ここで、右辺の第2項は、通常の遅延ポテンシャルを与えるものであるが、注目すべきは、第1項である。この項は、通常の遅延ポテンシャルの導出法では出てこないものである。第1項は、括弧の中身について、$${t' \to \infty}$$と$${t' \to -\infty}$$の場合の差分をとるのだが、このような、無限過去・無限遠の境界における値は、通常、深く考えずにゼロと見なしがちである。ところが、今考えている等加速度運動する電荷の場合、これを慎重に取り扱う必要があるのだ。第1項の分母で$${t = 0}$$とすると、
分母 $${= -c^2t' - \bold v\cdot\bold r_n}$$
となるが、$${t'\to-\infty}$$の極限をとると、$${\bold v \to c \hat{\bold r}_n}$$、また、$${r_n \to c|t'| = -ct'}$$となるため、
分母 $${\to -c^2t' - c\hat{\bold r}_n\cdot\bold r_n = -c^2t' - cr_n\to 0}$$
となってしまう。従って、第1項はゼロとみなすことができない。第1項のうち、$${t' \to \infty}$$の方は明らかに寄与しないので、第1項に対応するポテンシャル勾配($${\nabla V^\infty}$$とする)は、$${G}$$に式13を代入して、
$${\displaystyle \nabla V^\infty = -\frac{qc}{4\pi\varepsilon_0}\lim_{t'\to-\infty}\frac{\bold r_n\delta(ct-ct'-r_n)}{cr_n^2-r_n\bold v\cdot\bold r_n}}$$ 式19
となる。さて、$${t' \to -\infty}$$の極限で右辺がどうなるか、きちんと評価してみよう。右辺に現れる各項を$${t'^{-1}}$$の冪で表して整理すると、結果的に、
$${\displaystyle \nabla V^\infty = -\frac{q}{2\pi\epsilon_0}\frac{\delta(ct+z)}{s^2+b^2}\lim_{t' \to -\infty}\bold r_n}$$ 式20
となる。従って、電場の動径方向は、
$${\displaystyle E^\infty_s = -\nabla_sV^\infty = \frac{q}{2\pi\varepsilon_0}\frac{s}{s^2+b^2}\delta(ct+z)}$$ 式21
となった。これは式2と同じ式である!電場の$${z}$$成分は、ベクトルポテンシャルの寄与も入れて計算すれば、ちゃんとゼロになる。
ここで着目すべきは、式21の右辺に現れているデルタ関数である。観測点の座標が$${ct+z=0}$$を満たすときには電場の寄与が存在するが、それを満たさないときはゼロとなる。この$${ct+z=0}$$の条件は、電荷の事象の地平面そのものである(下図)。

青線は純粋な等加速度運動、赤線はtruncatedな場合に接続した等速運動である。
原点にいる観測者にとっては、式21の電場は、あくまで$${ct+z=0}$$の直線上に電荷がある場合にのみ現れるものであって、電荷がその直線からほんの少しでもずれていると、それはまったく見えなくなる。純粋な等加速度運動の場合、上図の青線で示したように、過去に遡ると、電荷は$${ct+z=0}$$の直線に漸近していくが、これはあくまで漸近であって、電荷がその直線上に乗ることは決してない。つまり、電荷の等加速度運動として、上図の青線の軌道で考える限り、式21の電場は導出できないことになる。
Crossの論文の主張をまとめると、以下になる(これはあくまで私の理解に基づく):
リエナール・ヴィーヘルトポテンシャルの通常の導出法では、電荷が無限遠・無限過去にあるとき、ポテンシャルはゼロになることが暗に仮定されているが、この仮定が成り立たない場合がある。
それは、電荷が無限過去・無限遠に光速で動いている場合で、一様等加速度運動がまさしくそれに該当する。
そのような運動を考える場合、通常の遅延ポテンシャルから議論を始めると、無限過去・無限遠の寄与が出ないので、その部分のポテンシャルは別立てで考える必要がある(式18第1項)。
うむ。理解できた(と思います)。
では、論文1, 2で議論されたtruncatedな運動で考えると、無限過去・無限遠の寄与がどうして自然に導出されたのでしょう?Jerroldが導出した電場は、元をたどれば、通常のリエナール・ヴィーヘルトポテンシャルから導出したことになるが、Crossの結論との関係はどうなのか?
私の理解するところによる解答は、truncatedな運動では、等速・等加速の接続点を無限遠にシフトさせて極限をとる操作において、事象の地平面$${ct+z = 0}$$を横切る点(図12に示した赤丸)が常に存在するから、となる。純粋な一様等加速の場合とは違って、truncatedな場合では、初めから$${ct+z = 0}$$に乗る電荷からの寄与が常に存在するようになっている。このように、無限過去・無限遠の電荷の寄与を導出するために、式18第1項に立ち戻らずとも、極限のとり方を物理的に工夫することでも、対応できるということだろう。
おわりに
以上、一様等加速度運動をする電荷のガウスの法則の見かけ上の破綻と、それが回復する仕組みを見てきたが、本稿を読んでいただいた方も、古典電磁気学の奥深さを実感できたのではないだろうか。古典電磁気学では、点電荷の自己相互作用や放射の反作用などでパラドックス的な問題がいろいろ知られるが、それらは、本来量子論的に取り扱うべきものを無理やり古典論で取り扱おうとすることに起因していることが多い。しかし、今回考えた問題のように、電荷の巨視的な運動に関わる問題でも、一見不可解で、意外なところから解決策が示される問題がけっこうあるのだ。数十年間解けなかった原因が、単純な前提の見落としや勘違いで、そこに気付きさえすれば、平易な計算で解決できることがあるというのも、純粋な数学にはない、物理学特有の面白いところである。
