翻訳の仕事を通して見た、ここ半世紀の数学と物理学の動向
2024年11月、エンジニアの方々(と一般の方も)に向けて、講演をさせていただく機会がありました。タイトルは、「翻訳の仕事を通して見た、ここ半世紀のサイエンスの動向」。とくに、「数学と物理学」「遺伝学」「生物学と人類学」という三つの領域の動向について、お話させていただきました。
最新のサイエンスの動向ということになりますと、当然、最先端の話に触れることになります。サイエンスに興味はあるけれど、なかなか手が出ない……という方たちのために、理論や実験の具体的内容にはあまり立ち入らず、わたし自身が、この間「すごいなー、面白いなー」と思った動きに絞り込んで、俯瞰的に、あるいは模式的に、お伝えすることを試みました。
その講演でお話したことを、「数学と物理学」「遺伝学」「生物学と人類学」に分けて、noteにアップします。
私が大学の理学部に入ったのは1975年ですから、来年でちょうど50年ということになります。この間に私は、学部から大学院、ポスドクを経て翻訳業に転じ、長年サイエンス分野の本を手がけてきました。そこで本日は、この半世紀間に、私が見てきたサイエンス分野の動向、なかでも、数学と物理学、遺伝学、生物と人類学という、三つの領域の動きについて、お話させていただこうと思います。
はじめに、数学と物理学の動向です。と、軽く言ってしまいましたが、最新の動向となりますと、どうしても現代数学、現代物理学の最先端の話にならざるをえません。須藤さんからは、本日の聴衆のみなさんは基本的に理系人なので、サイエンス系の話はなんでも興味を持って聞いてくださると思いますよ、と言っていただいたのですが、数学と物理学の最先端となりますと、理論や実験そのものの中身を三十分やそこらでお話しするためには、私はまったく力不足ですし、実際、そんなことができる人はいるのだろうか、とさえ思います。
しかしだからといって、数学と物理学の新しくて魅力的な動きを紹介できないとしたら、物理出身の私としてはあまりにも残念です。そこで本日は、専門的な内容にはあまり立ち入らずに、何がどう変わったのかを、俯瞰的に見ていただくことを目指したいと思います。難しそうな専門用語も少しは出てきますが、どうかそこはあまり気にせず、大きな変化が起こっているんのだなぁ、と、その眺めを楽しんでいただければと思います。最先端の光景をご覧いただけるよう、がんばります!
さて、まずは数学です。私が大学に入った頃は、数学はどんどん細かい分野に枝別れして、専門化が進んでいるように見えました。実際、数学者同士であっても、研究している領域が違えば言葉が通じない、などとも言われていました。
学問の進展にともなって分野が細分化し、専門化が進むのは無理もないことですし、その傾向はずっと続いていくんだろうな、と私は漠然と思っていました。ところが、そうではなかったのです。私が最初にその流れの変化を感じたのは、「フェルマーの最終定理」が証明されたときのことでした。証明は1995年ですから、私が大学に入学してからちょうど20年後にあたります。
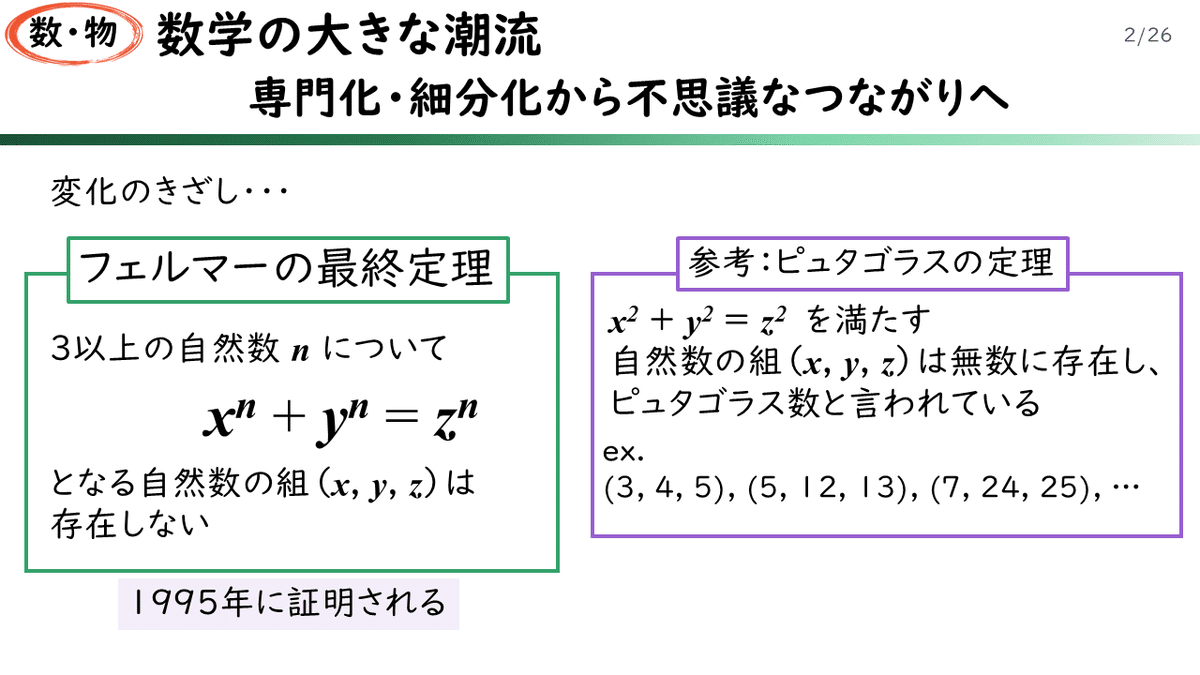
「フェルマーの最終定理」というのは、3以上の自然数nについて、xn+yn=znという等式が成り立つような自然数の組(x, y, z)は存在しない、というものです。17世紀のフランスに生きたピエール・ド・フェルマーという数学者が、3世紀のエジプトはアレクサンドリアに生きたディオファントスという数学者が書いた『算術』という本の、ピュタゴラスの定理のくだりを読んでいたんです。こちらに参考として、中学校で習う三平方の定理、いわゆるピュラゴラスの定理を示しました。直角三角形で、直角を見込む二辺の長さの二乗の和は、斜辺の長さの二乗に等しい、というあれですね。この関係を満たす(x, y, z)は無数にあることがわかっており、ピュタゴラスの「三つ組数」と言われといわれています。ディオファントスは、このピュタゴラスの定理を懇切丁寧に説明していたのでした。
フェルマーは、その部分の余白に、ピュタゴラスの定理の二乗のところを「3以上」に変えると解がなくなるとして、「自分はその驚くべき証明を見つけたが、余白が狭すぎるのでここに書くことはできない」とメモしたのでした。フェルマーは証明を見つけたと言いましたが、その後350年ものあいだ、誰ひとりそんな証明を見つけることはできませんでした。ようやく20世紀も末の1995年になって、イギリスの数学者アンドリュー・ワイルズが証明を成し遂げたのです。
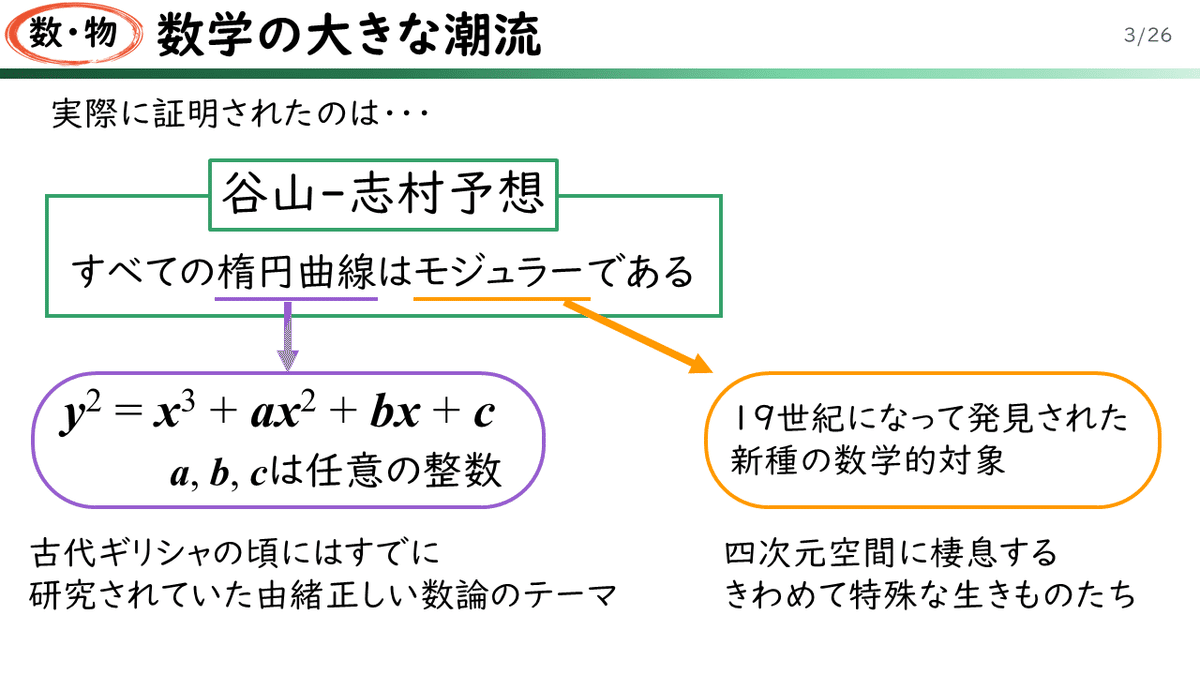
実は、ワイルズが証明したのはフェルマーの最終定理そのものではなく、谷山=志村予想と言われるものでした。「すべての楕円曲線はモジュラーである」、というのがそれです。楕円曲線というのは、y2=x3+ax2+bx+c という方程式で表されるもので、古代ギリシャですでに研究されていた、由緒正しい数学のジャンルです。一方、モジュラーというのは ようやく19世紀になってフランスの大数学者ポアンカレが発見した、きわめて特殊な数学的対象です。あまりにも奇妙な性質を持つので、ポアンカレ自身、なかなかその存在を信じられなったという、いわくつきの世界です。
楕円曲線とモジュラーは、一見すると似ても似つきません。しかし、そうであればこそ、もしも「すべての」楕円曲線がモジュラーだというのが本当なら、それは大変なことです。たとえて言えば、海に隔てられた二つの大陸に橋がかかり、自由に行き来できるようになってみたら、それぞれの大陸に住む人々の姿形はまるで違うし、社会制度もまったく違うのに、実はその人たちは一対一に対応していて、いわば同一人物だった、というようなものです。そうなると、数学的には、一方の大陸では取り扱いの難しかった問題が、他方の大陸にもって行くとあっさり解けてしまう、というようなことが起こります。
この予想はもともと、1955年に谷山豊さんという若い数学者が、もうすこしゆるいかたちで言い出したのですが、谷山さんはその後すぐに亡くなってしまいました。それから十年ほどかけて、谷山さんの盟友だった志村五郎さんという数学者が、谷山さんが言ったことを、数学的な「予想」と言えるところまできっちり詰めて作り上げたのでる。谷山=志村予想は、もしもそれが正しければ、数学に激震が起こるほどの大予想でした。そんなわけで、「もしも谷山=志村予想が成り立てば、これこれのことが言える」という論文がどんどん出て、ひとつのジャンルになったほどです。そうなると、もしも万一、谷山=志村予想が成り立たないということが証明されれば、この予想の上に積み上げられた仕事は総崩れになるわけです。
それに加えて、1985年になって、もしも谷山=志村予想が正しいことが証明されれば、フェルマーの最終定理が自動的に証明されてしまう、ということがわかったのです。つまり、谷山=志村予想を証明すれば、350年という長い歴史を持つ、「フェルマーの最終定理」も証明したことになる、というおまけがついたのです。アンドリュー・ワイルズは、まさにそれを成し遂げたのでした。
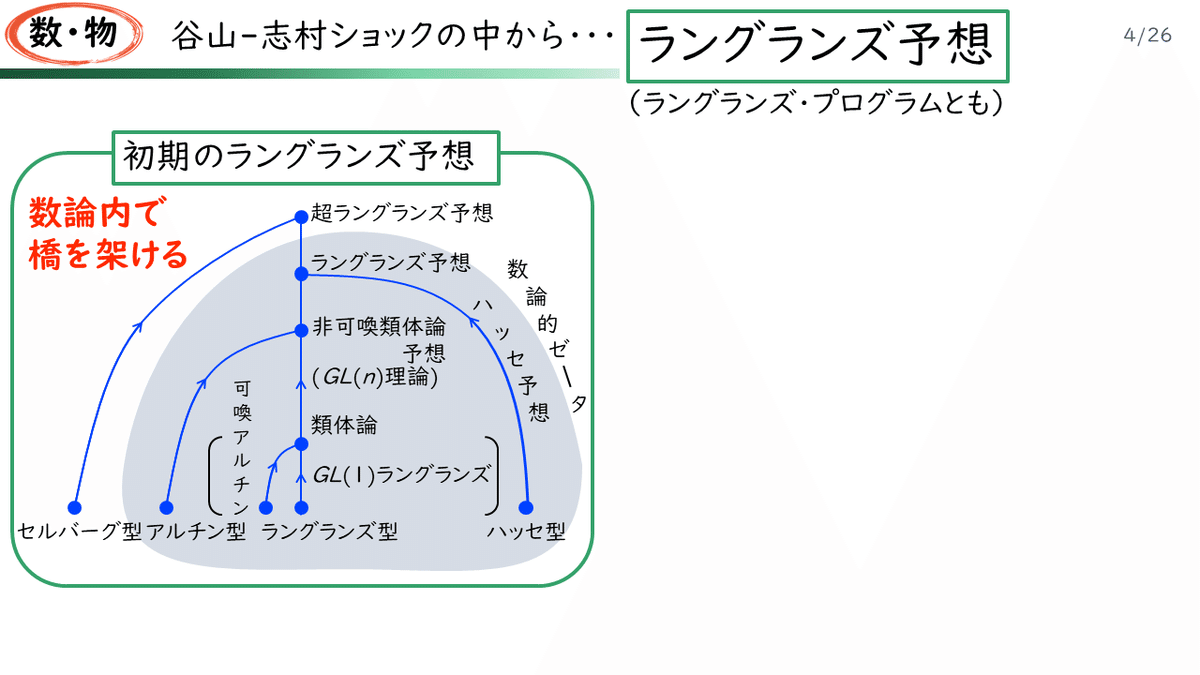
さて、まだワイルズによる証明がなかった頃、プリンストン大学の数学者ロバート・ラングランズが、谷山=志村予想に衝撃を受けて、「ラングランズ予想」と呼ばれるものを打ち出しました。ラングランズ予想は、今日、ラングランズ・プログラムとも呼ばれます。
もともとのラングランズ予想は、「数論」という分野の内部であちこちに橋をかけるというものでした。「数論」とは、整数に関係するような数の体系の性質を研究する分野で、「フェルマーの最終定理」も数論の問題です。

ところが、ラングランズ・プログラムは、その後、数論の分野だけにとどまらない驚くべき進展を遂げ、しだいに他の大陸にも橋がかかるようになったのです。数論大陸から、有限体Eの曲線大陸、そこからリーマン面大陸へ、さらには、なんと! 物理学にまで橋が架かったのです。これはごく最近の進展です。
その物理学は、この図には「量子物理学」と書きましたが、もっと具体的には「ひも理論」です。一般には、素粒子は、サイズのない数学的な点だと考えるんですが、ひも理論では、素粒子は、ひものように長さのサイズがあると考えます。すると、数学的な点だと考えたときに出てくるやっかいな問題が解消するからなのですが、それだけでなく、今日、ひも理論は、重力まで含めて、自然界の力をすべて統一する理論の最有力候補とみなされています。
重力を他の力と統一することは、言ってみれば、物理学の聖杯のようなものなのです。
ラングランズ・プログラムは、20世紀後半から21世紀もだいぶ進んだ今に至るまで、数学のひとつの大きな潮流となって驚くべき成果を挙げています。半世紀前には、数学はこのまま専門分化が進んでいくのかなぁ、と思っていましたが、そうではありませんでした。数学のさまざまな領域、地図で言えば大陸のようなものに橋がかかったのです。とくにすごいのは、物理学にまで橋がかかったことです。そのおかげで、数学的に扱いにくい問題に、物理学のこなれた手法でアプローチできるようになっています。
物理学はこれまでずっと、過去の数学者たちが作りあげたものを再発見して、道具として使わせてもらうということを続けてきました。一方的に、数学のお世話になるばかりだったのです。それが今では、物理学が数学にインスピレーションを与え、道具も提供しています。数学と物理学が、双方向に影響を及ぼし合うようになったと言えるでしょう。
ここで数学の動向をまとめておくと、半世紀前には、専門分化が進み、分野が違えば言葉が通じないなどと言われていましたが、今では、海を隔てた大陸のように見えていた分野に橋がかかり、魅力的なつながりが姿を現しています。しかもそのつがなりが、物理学にまで及んでいるということです。
実は、物理学の分野の内部でも、ラングランズ・プログラムとは別に、いろいろとつながりがつくようになっています。
私がいた京都大学の物理教室は、第一教室と第二教室という、大きくふたつの組織に分かれていました。今も組織としては分かれています。物理学の分野としては、第一教室は、物性物理学という、マクロな物質の性質について調べる研究室が集まっています。一方の第二教室は、素粒子、原子核、宇宙について調べる研究室が集まっています。私は第二教室のほうにいたのですが、当時、第一教室と第二教室のあいだには、かなり距離感がありました。
また、第二教室の中でも、素粒子と原子核と宇宙は、それぞれ扱う対象のスケールが大きくに違うし、用いる手法もなにかと違っていました。スケールということだけ考えても、素粒子は数学的な点でしたし、原子核は、それよりはずっと大きな複雑な世界ですし、宇宙は、まさしく宇宙論的な最大スケールの現象を扱うわけです。

ところが、私がいた当時から、まず第二教室内で、素粒子、原子核、宇宙の垣根がなくなりはじめました。それを象徴する出来事が、インフレーション理論の提唱です。当時、京都大学の助手だった宇宙論の佐藤勝彦さんが言いだしたのです。インフレーション理論は、宇宙のごく初期に関するもので、「インフレーション」というキャッチーな名前をつけたのは、アメリカのアラン・グースという物理学者ですが、実は、佐藤勝彦さんは、グースよりも先に、もっと地味な名前で、この理論を打ち出していたんです。そのことは、今では世界的に認められています。
そのインフレーション理論によれば、ビッグバン理論の「宇宙はあるとき膨張を始めた」という大雑把な宇宙の始まりには、実は前工程があり、宇宙はまず、一瞬のうちにとてつもない大きさになったということになります。この図の、水色の部分、宇宙のサイズがいきなり大きくなる部分です。その前工程を考えることで、宇宙論を悩ませていたいくつかの問題がきれいに解決されました。インフレーションのプロセスは、ミクロの世界を支配する量子的なものです。量子の世界に独特のゆらぎのために、われわれの宇宙はひょっこりと生まれて、激烈なインフレーションを始めたということになります。
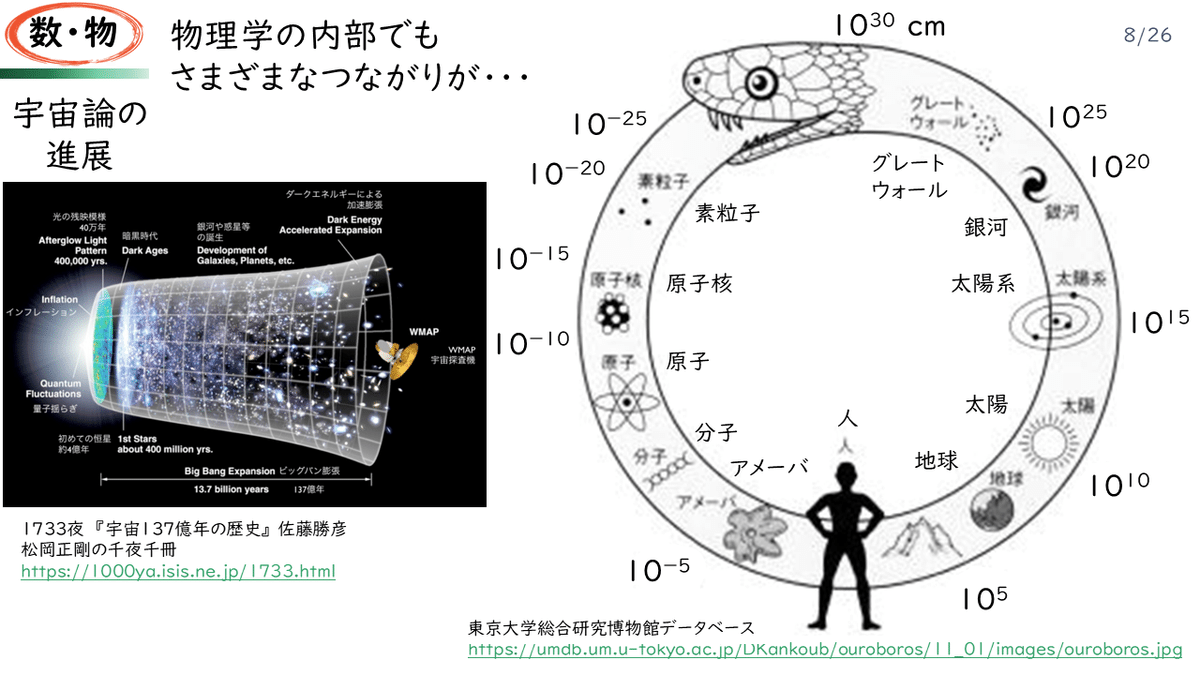
インフレーション理論はすみやかに受け入れられました。そのこともあって、1980年代から90年代にかけてさかんに描かれたのが、上の図の右側のウロボロスの絵です。ウロボロスというのは、自分の尻尾を噛んでループ状になったヘビのことです。ヘビの頭である最大スケールの宇宙から、どんどんスケールの小さくしていって、素粒子の最小スケールにまで達すると、結局、最大スケールの宇宙につながっていた、というわけです。ヘビをまっすぐ伸ばしたときのように離れているのではなく、頭と尻尾がつながっていた。宇宙というのは、実はとても量子的な世界なんですね。これにより、素粒子、原子核、宇宙がつながり、研究の面でも分野の垣根はなくなった感があります。

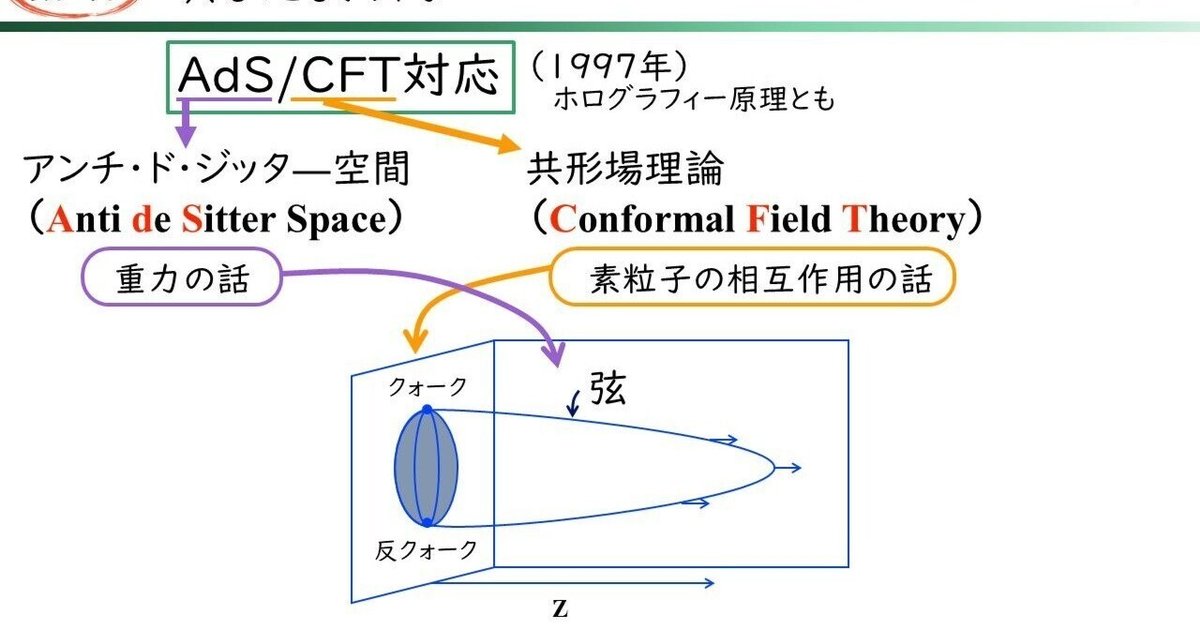
物理学にはこのほかにもいろいろと強力なつがなりが生まれているのですが、本日は、そのうちのひとつ、今もっともホットな「AdS/CFT対応」をご紹介したい思います。さて、ここでいよいよ「物理学最先端!」という感じの、難しげな専門用語が出てきますが、どうかご心配なく。大丈夫です!
AdSというのは「アンチドジッター空間」の略で、重力の話です。一方、CFTというのは「共形場理論」の略で、素粒子の相互作用の話です。つまり、重力と、素粒子の相互作用とのあいだに、ある種の対応関係につくというのです。そのおかげで、込み入った素粒子の相互作用の問題が、シンプルな弦(ひも)の振る舞いに焼直せたり、逆に、重力のややこしい問題が、素粒子の相互作用に焼直せたりするのです。
この対応関係は、「フォログラフィー原理」と言われることもあります。なぜかというと、図の左側、素粒子の相互作用の世界の次元が、重力の世界の次元よりも、一次元低くなっているからです。クォークと反クォークの棲む世界は、二次元の平面で表されています。その平面に、Z方向に一次元足した三次元空間が、重力の世界として示されています。「ホログラフィー」というのは、みなさんご存知のように、二次元の平面の中に、三次元の像を描き出すために必要な情報がすべて含まれています。それと同様に、重力に関する情報が、一次元低い物質の世界に含まれているというわけです。
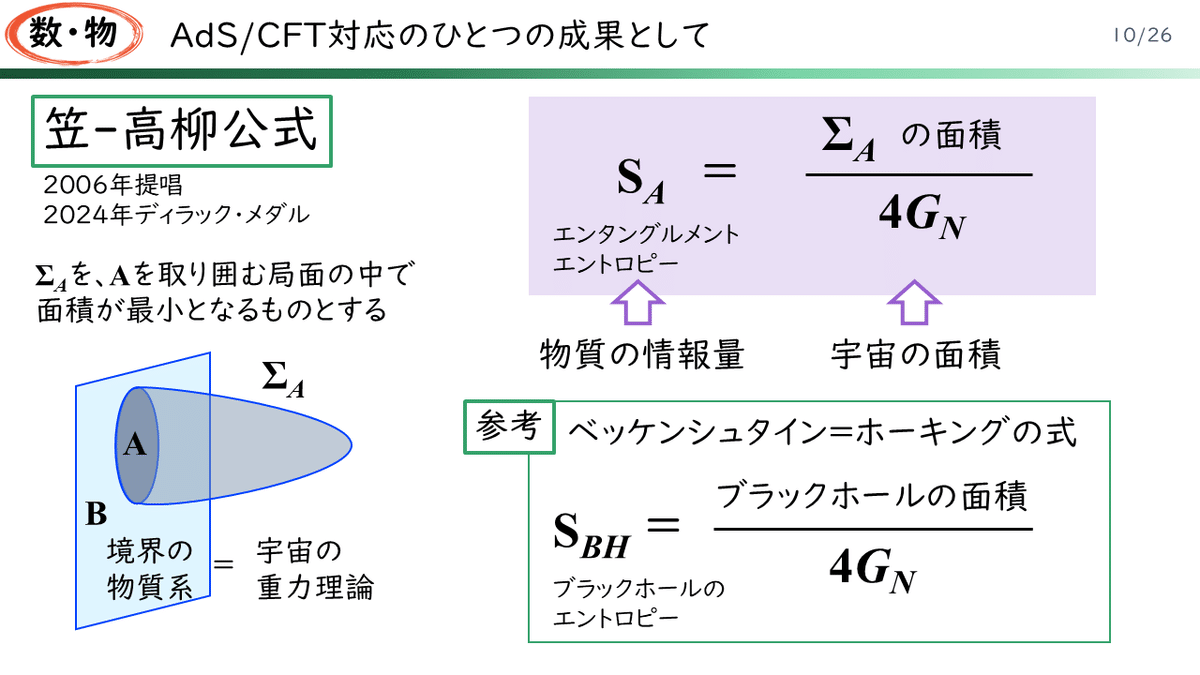
AdS/CFT対応のひとつの成果として、2006年に提唱された「笠=高柳公式」というものがあります。この仕事により、現在プリンストン大学教授の笠真生(りゅう・しんせい)さんと、今は京都大学基礎物理学研究所教授と東京大学カブリ数物連携宇宙研究機構にも所属される高柳匡(たかやなぎ・ただし)さんは、今年、ディラック・メダルという栄誉ある賞を受賞なさっています。
笠さんは物性物理学の人、高柳さんは素粒子の人です。この公式は、物性と素粒子のあいだの垣根もなくなっているという、この間の動向を象徴するものでもあると思います。
ここでも専門的なことは抜きにして、何と何が結びついているかを見ていただきたいと思います。
=(等号)の左側にあるSa は、エンタングルメント・エントロピーといわれるものです。エントロピーというのは、1980年代ぐらいには、物理学の範囲を飛び出して世間的にもよく見聞きした言葉で、みなさんもきっと聞き覚えがあるかと思います。机がだんだん散らかっていくことを、「エントロピー増大の法則」なんて言ったりしました。乱雑さと結び付けられていた、なんとなく手あかのついた言葉、というイメージがあるかもしれません。
しかしあれから半世紀、今やエントロピーは、情報理論と結びついて新たな重要性を帯び、幅広い分野でキーワードになっています。たとえば高柳さんは、エントロピーのことを「隠れた情報」だという言い方をよくなさいます。情報として存在はしているのだけれど、「隠れている」あるいは、われあれが現状「見ていない」情報、という感じでしょうか。
エンタングルメントというのは、量子の世界に独特の絡み合いです。そのエンタングルメントにかかわるエントロピーが、アンチドジッター空間の、図に示したコーン型の図形の「面積」を、普通の「重力定数」で割ったものになっている、というのです。物質の世界と宇宙がダイレクトに繋がるというのも驚きですが、エントロピーが面積で表されるというのも衝撃的です。というのは、エントロピーというのは、普通は体積と関係していると考えられているからです。
実は、1970年代に、車椅子の物理学者スティーヴン・ホーキングが、ベッケンシュタインという物理学者とともに、ブラックホールのエントロピーを表す式を発見しました。ブラックホールのエントロピーは、なんと、ブラックホールの表面積で表されるのです。「なんとシンプルで美しく、驚くべき式か!」ということで、ホーキングは、この発見をとても誇りに思い、自分の墓石にこの式を刻ませるよう言い残したほどでした。実際、ウェストミンスター寺院に置かれた彼の墓石には、この式が刻まれています。
笠=高柳公式は、ベッケンシュタイン=ホーキングの式を大幅に拡張して、「情報は面積だ!」、「境界の物質系=宇宙の重力理論だと」いう関係が、ブラックホールだけでなく、一般の宇宙で成立することを示していると言えます。

ここで、この半世紀の数学・物理学の動向をまとめておきましょう。
半世紀前には専門化・細分化が進むのは当然なのかな、と思ってましたが、その後、あちこちで驚くべきつながりが浮かび上がり、魅力的な進展が起こっているということです。
