東北大理系数学2007
今回は、東北大理系数学2007の解説をしていきます。
大問1 漸化式、整数
(1)、(2)はどこかでみたことがあるような問題です。
解答にかかれていますが、実は、整式の世界でも、modの概念を考えることができます。これを使えば、非常に簡単に解けていきます。これについては、新しく特集記事を書く予定です。
(3)は正直、著者はかなり苦戦しました。もっと、良い解法がありそうですが、これが無理のない解答じゃないかなと思います。

大問2 図形
これはかなり簡単な問題で、大問1(3)で使い過ぎた時間を戻してくれそうです。
5π/12をばらすところがポイントですが、これは受験生なら解けていることでしょう。

大問3 極限(関数)
(1)はいつも通り、「単調性と中間値の定理」です。
(2)は、x=e^(1/n)を入れたらうまくいくことに気づくかどうかです。似たような経験をしたことがあれば、この発想もいけるでしょう。

大問4 最小値(線分の長さ)
これはなかなか面倒くさい問題です。
とりあえず、対称性を考えてやらないと埒が明きません。
直線Lが正方形のどこと交わるかで、3つの場合分けが生じます。面倒がらず計算していけば、求まります。


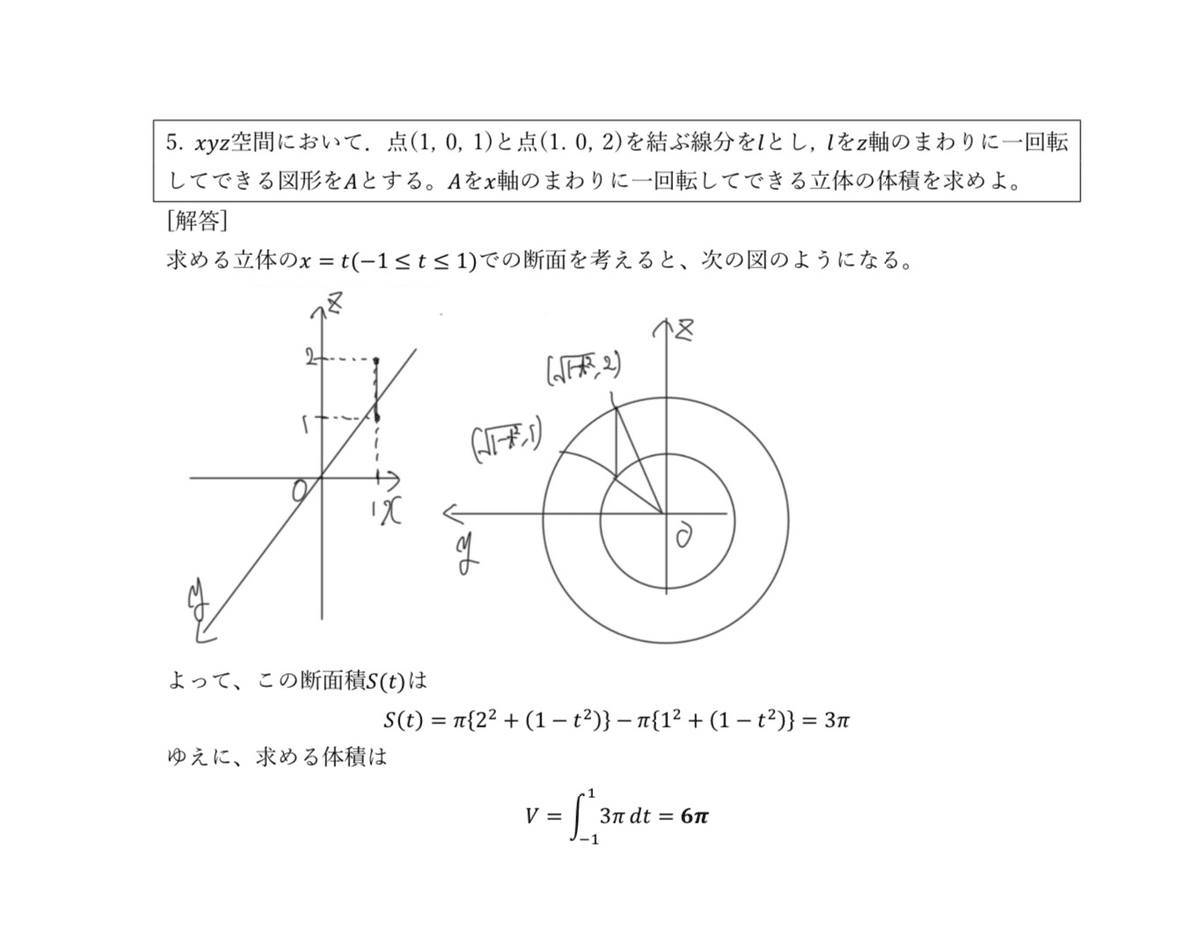
大問5 積分(断面積)
これは、断面積さえイメージをつかみ、図示すれば、あとはどうということありません。
これは落とせないでしょう。
大問6 漸化式(積分)
(1)、(2)はオーソドックスで、おそらくは解けたでしょう。
問題は(3)です。解答では、帰納法で極限を示していますが、この方法を使ったのは、著者は初めてです。正直面くらいました。
これに至る過程は次のような感じです。
①まず、極限をn=1から順に計算していきます。
②分子が変わらず、分母が何か規則性がありそうだなと思う。
③予想した極限にいくことを帰納法でしめすのか?と思う。((2)で漸化式だしてるし)
こんな感じで解答の発想がでてきています。が、この発想に至るのに15分くらいはかかっているので、試験場では相当厳しい問題だと思います。


こちら、解答解説に問題だけのページを追加したpdfとなっております。
ご活用ください。
のちに、youtube のほうに解答解説をさらに詳しく解説した動画をupする予定です!
また、補足説明や類題演習も考えていますので、よければフォロー、いいね等お願いします。
また、解説で分かりにくい箇所等、ございましたら、気軽にXにdmか、コメントお願いします!
この記事が気に入ったらサポートをしてみませんか?
