
【大乗仏教】背理法(帰謬法)
中期中観派に入る前に「背理法(帰謬論証)」と「古代インドの論理学」に少し触れておきたいと思います。今回は「背理法(帰謬論証)」を見ていきます。龍樹後の中期中観派の仏護(ブッダパーリタ)が帰謬法を用いて龍樹の説法を論理的に説明しようと試みます。
○背理法(帰謬法)
ある立言$${r}$$が真であることを証明したい時、まず$${r}$$が偽であるとする非$${r}$$、つまり$${\bar r}$$を仮定し、この仮定から不合理な結論(明らかに偽であることが知られていたり、自己矛盾である結論)を演繹します。
▽定言論証例
$${p}$$:煙のあるところには、火がある
$${q}$$:この山には、煙がある
$${r}$$:故に、この山には、火がある
※この定言論証式を助け、反証する帰謬式は次のように書けます。
▽帰謬論証例
$${p}$$:火のないところには、煙がない
仮定$${\bar r}$$:この山には、火がない
(と仮定すると)
偽なる結論$${\bar q}$$:この山には、煙がない
(という不合理に陥る故に、この山には火がある)
※「この山には火がない」は立論者自身にとって真ではなく、あくまで仮定されたものです。
※演繹された「この山には煙がない」という結論は立論者・反論者の両方にとって偽となります。
※背理法(帰謬法)はその性質上、必ず仮言的であり、結論は真ではない誤知です。
帰謬法はインド論理学(ニヤーヤ学派の論理学)でも定言論証の補助手段であり、それは含意的にそれ自身の小前提(仮定)と帰結との矛盾命題を反証します。つまり、上記の帰謬式「pかつ非rならば、非qという不合理に陥る」は、必然的に「pかつqならば、rである」の真であることを反証することになります。
インド論理学者(ニヤーヤ学派)は帰謬法がある立言の真なることを決定するために重要な熟慮であり、ある立言を直接的に論証する定言的論証式の補助手段としても極めて有効であると認めていたのですが、帰謬法そのものを確実な論証式としては認めなかったとされます。理由は小前提が仮定であり、成立していないためです。
※豆知識
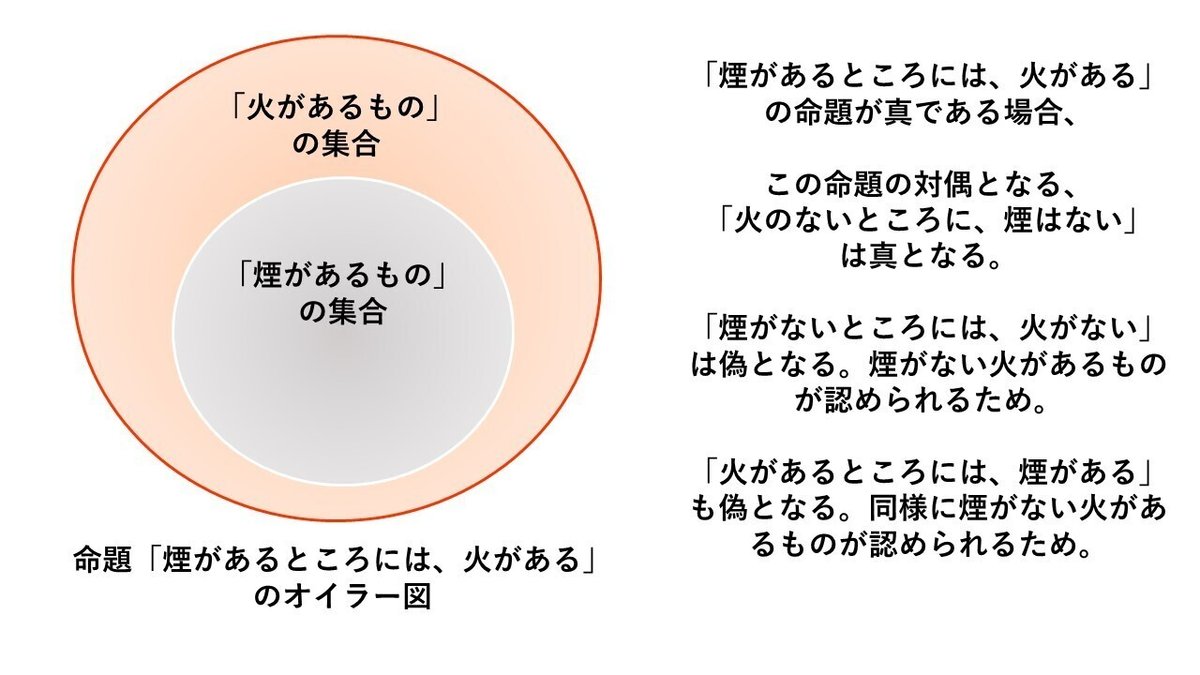
高校数学で「必要条件」「十分条件」を学んだと思います。上の図を例にしますと、「煙があるもの」は「火があるもの」の十分条件であり、「火があるもの」は「煙があるもの」の必要条件となります。
