ゲームエンジンで体感する外積

Hiko

2021年3月20日 23:32

前回の記事では「ゲームエンジンで理解する内積」と題して内積についてみてきました。

内積と比較すると外積が示す値は直感的に理解しやすいため、今回は外積の意味を理解するというよりも、外積がどのように変化するかを観察することで外積の効果を体感できるように解説します。

外積の概念や定義は何となく把握できている前提として進めていくため、改めて外積について確認したい場合は以下のサイトを参照してください。とても分かりやすくまとまっています。

それでは早速ゲームエンジンのUnityを使って外積の振る舞いを見ていきましょう！

位置で変わる外積の符号

下図の例では3D空間上にスフィアを配置し、赤をベクトルa・青をベクトルb・緑をベクトルaとbの外積として表しています。

多くの外積の解説サイトでは「右ねじの法則」に従って外積ベクトルの向きを表していますが、一般的な数学・物理の世界では右手座標空間を使用しているのに対し、Unityでは左手空間座標系を使用しているため逆向きの外積ベクトルとなります。Unityのドキュメントからも"left hand rule"を採用していることが読み取れます。

では左手空間座標系ではどのように向きを知るかというと「フレミング左手の法則」を用いて親指を左ベクトル、人差し指を右ベクトル、中指を外積ベクトルの向きとして把握するようにしています。

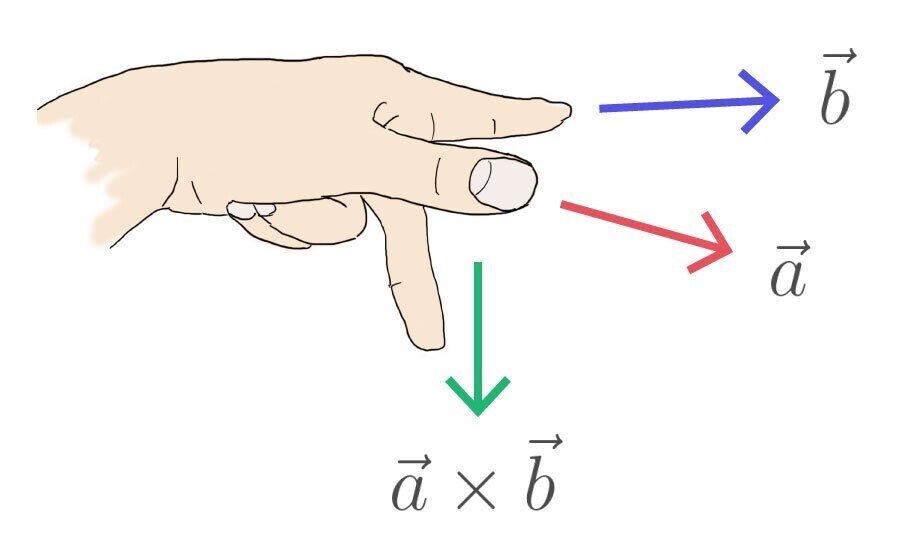
上図の例では外積は下向きですが、ベクトルaの向きが反対になると外積は上向きになることが分かります。では本当にそうなるのかUnityで見ていきます。Unityで外積を扱う場合は、Vector3.Cross(Vector3 lhs, Vector3 rhs);を使います。今回の例ではVector3.Cross(a, b)としました。

コードとしては以下のようになります。red、blue、green、origin(white)はそれぞれの色のスフィアのゲームオブジェクト、xxLineはオブジェクト間を結ぶLinerendererを割り当てています。

    void Update() {
       redLine.SetPosition(0, origin.transform.position);
       redLine.SetPosition(1, red.transform.position);
       blueLine.SetPosition(0, origin.transform.position);
       blueLine.SetPosition(1, blue.transform.position);

       Vector3 cross = Vector3.Cross(
           red.transform.position,
           blue.transform.position
       );

       green.transform.position = cross;  
       
       greenLine.SetPosition(0, origin.transform.position);
       greenLine.SetPosition(1, cross);
   }

実行してredスフィアを動かしてみると以下のようになります。白いスフィアは基準値として原点(0, 0)に配置しています。

redスフィア(ベクトルa)の高さを変えた状態で移動させると、blueスフィア(ベクトルb)とそれぞれ直交する向きにgreenスフィア(外積)が移動します(下図)。この挙動から外積の向きが「フレミング左手の法則」と一致していることが分かります。

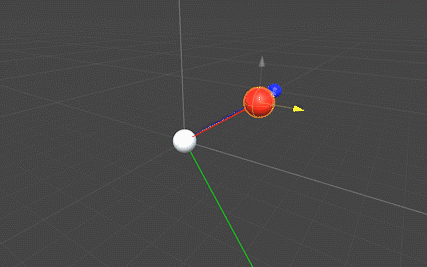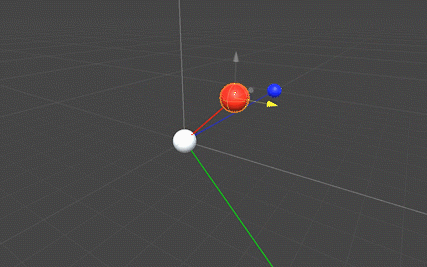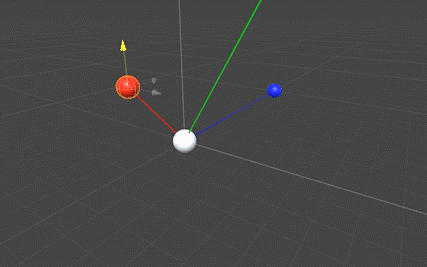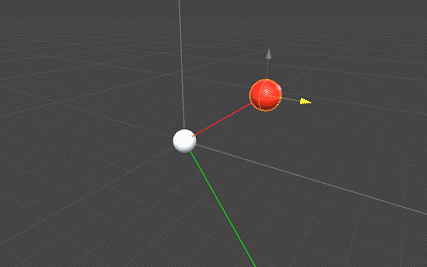
また、外積を示すgreenスフィアの座標を表示すると分かりますが、redスフィア(ベクトルa)とblueスフィア(ベクトルb)の位置関係=ベクトル方向の関係によってgreenスフィアのY軸の値の符号(+,-)が変わることが確認できます。

このことから2つオブジェクトの座標が分かれば、外積の符号を使ってお互いの向きの関係性を知ることができそうです。次の項では外積が示す符号と向き(位置)関係について詳しくみていきます。

解説に使用したコードはGitHubで公開しています。

向きを知る

外積の大きさは2つのベクトルで構成される平行四辺形の面積に等しくなることが知られています。証明は以下の新潟工科大学のサイトが参考になります。

式としては以下のようになります。

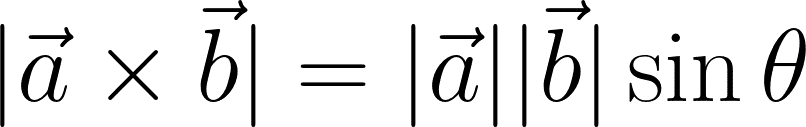
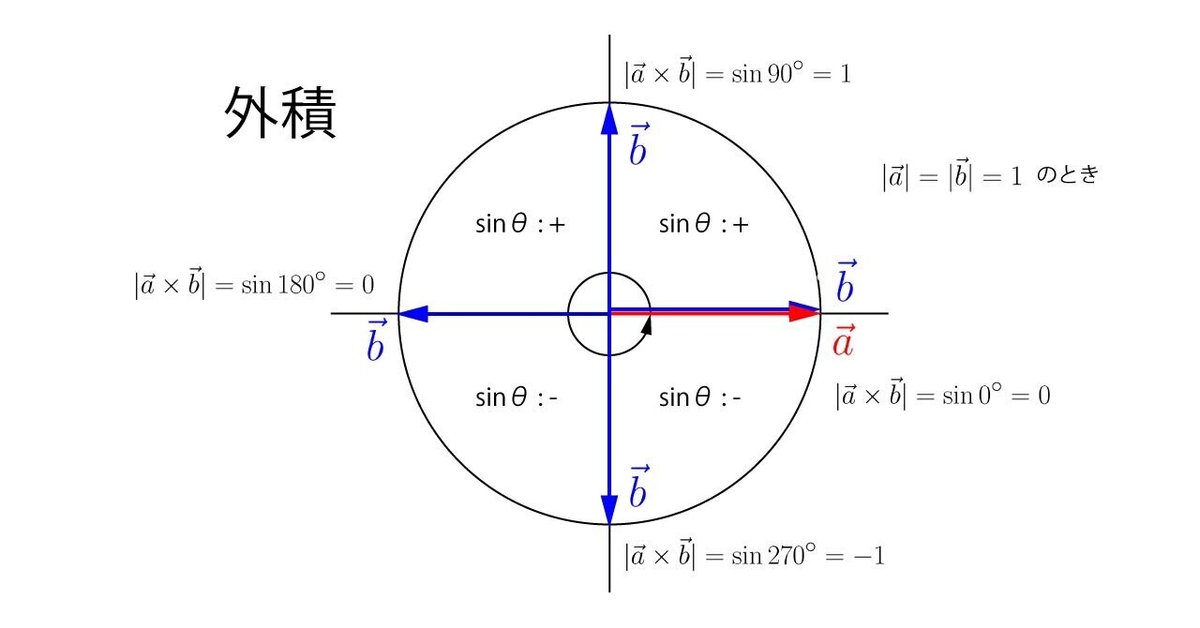
平行四辺形の面積は底辺×高さなので、|a|を底辺とすると|b|sinθは高さになるので外積の大きさが平行四辺形の面積の求め方と一致することが分かります。ではここで、ベクトルaとベクトルbの大きさが1のときの外積を考えてみます。そうすると上記の式は以下のようになります。

つまり、2つのベクトルを大きさ1の単位ベクトルに変換して外積を求めると、両者のなす角のsinθが得られることが分かります。

これは前回の記事の「ゲームエンジンで理解する内積」での内積で得られる角度と同じ考え方になります。そして、内積では2つの単位ベクトルからcosθが得られました。

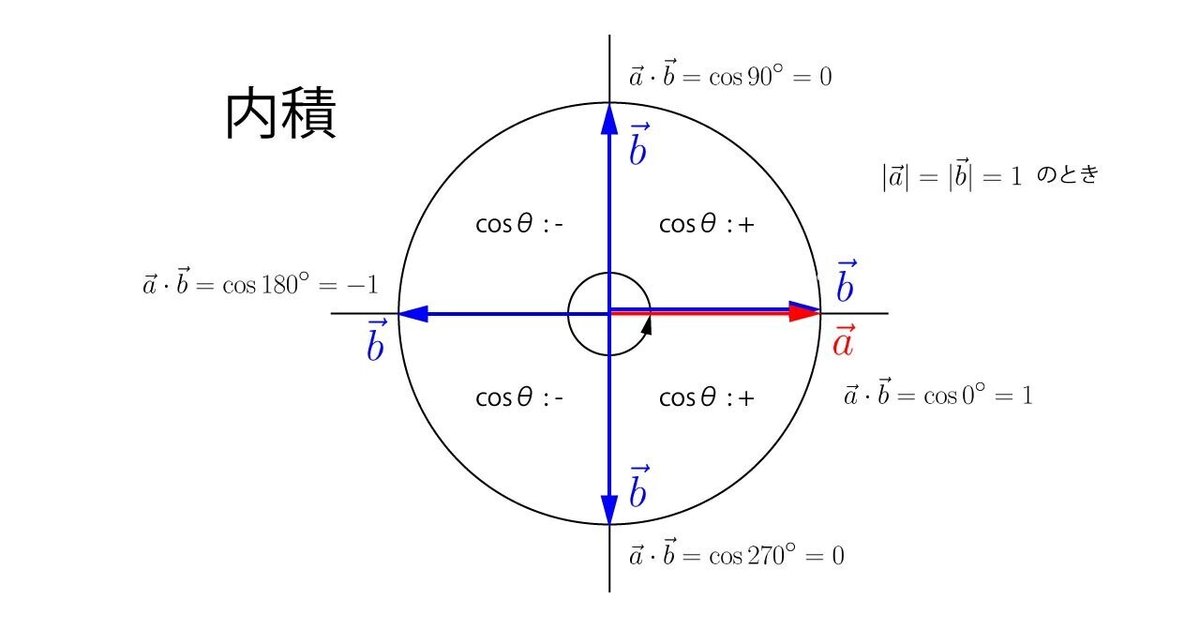
そうすると察しの良い方はお気付きかもしれませんが、内積と外積を用いると基準点から考えた2つのベクトルがなす平面上の完全な向きの関係を得られるようになります。

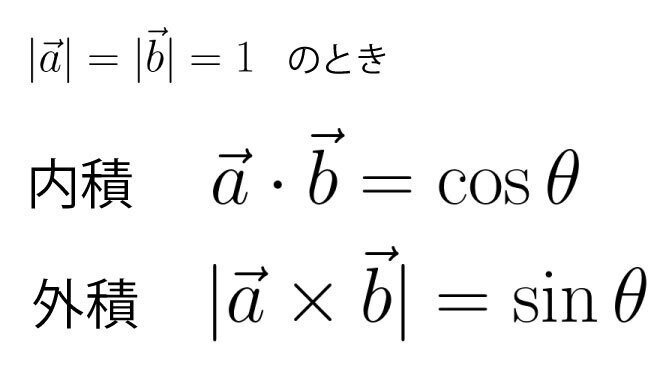
例えば内積のcosθだけでは0°～90°と270°～360°を区別することはできませんが、外積のsinθがあれば符号が変わるため判別することができます。このようにcosθとsinθを組み合わせることで、初めて平面上での2つのベクトルの向きの関係を把握することができます。

これを踏まえてUnityを使った応用例を考えてみます。プレイヤーの視線ベクトルをa、プレイヤーを基準とするターゲットの単位ベクトルをbとし、ターゲットとプレイヤーとの位置関係が変わったときにターゲットの色を変える処理を行います。コードは以下のようになります。

   [SerializeField] GameObject player = default;
   [SerializeField] GameObject target = default;
   [SerializeField] Text debugText = default;

   [SerializeField] Material mat1 = default;
   [SerializeField] Material mat2 = default;
   [SerializeField] Material mat3 = default;
   [SerializeField] Material mat4 = default;
   private MeshRenderer mesh;

   void Start() {
       mesh = target.GetComponent<MeshRenderer>();
   }

   void Update() {
       var a = player.transform.forward;
       var b = target.transform.position.normalized;

       var dot = Vector3.Dot(a, b);
       var cross = Vector3.Cross(a, b).y;

       debugText.text = "cosθ: " + dot.ToString("F2") + "\n" + "sinθ: " + cross.ToString("F2");

       if (dot >= 0) {
           if (cross >= 0) {
               mesh.material = mat1;
           } else {
               mesh.material = mat2;
           }
       } else {
           if (cross >= 0) {
               mesh.material = mat3;
           } else {
               mesh.material = mat4;
           }
       }
   }

Materialは判別可能な4色(種類)のマテリアルをアタッチしてください。debugTextは内積と外積の数値が位置によってどのように変化するかを確認できるように入れています。

外積の演算でVector3.Cross(a, b).yとしているのは、プレイヤーとターゲットが同じ高さのときに外積のy成分がsinの値になることを利用しています。本来であれば、Vector3.Cross(a, b).magnitudeで大きさを取りたいところですが符号が消失してしまうことや式を簡単にするためにこのようにしています。

実行すると以下のようになります。

こちらもコードはGitHubで公開しています。

今回の解説は「テラシュールブログ」さんの記事を参考にして作りました。ありがとうございます。

まとめ

本記事では外積の概念や定義にはあまり触れず、実際にUnityを使って外積の振る舞いを見てきました。これによって外積の作用・効果を雰囲気で感じていただけたでしょうか。

数式から意味を理解することは大切ですが、ときには手を動かすことで物体の挙動から意味を理解するアプローチもあっても良いかと思います。

また、向きを知る事例については実は内積や外積を使わずともUnityのVector3.SignedAngleで実現することができます。Vector3.SignedAngleは2つのベクトルと回転軸となる軸を引数に指定することで、2つのベクトルの角度を-180°～180°(360°)の範囲を得ることができます。

今回は外積の効果や振る舞いを体験するためにあえて外積を使って実現しました。もしかするとSignedAngleも内部的には内積・外積を使っている可能性もありますが、ベクトルの基本演算である内積・外積を使いこなせると表現の幅はぐっと広がるはずです。この記事が少しでも皆さんの理解の手助けになれば幸いです。🌱

参考

Unityでの角度計算のメソッドを紹介している記事です。角度を使って何かしたいときはとても参考になります。

この記事が気に入ったらサポートをしてみませんか？