ゲームエンジンで理解する内積

3DCG・ゲーム・シェーダー制作をやっていると何かと目にする内積ですが、「いまいち何だかよく分からん」「どう使っていいのか分からん」という方は多いかと思います。

ここではまず内積についての考え方を私なりに解説し、次にゲームエンジンであるUnityを使って内積がどの場面で活用できるかを説明していきます。

ゲーム制作だけでなく、数学として内積を理解したいという方に対しても手助けとなれば幸いです。それでは早速やっていきましょう。

内積の考え方

まず内積の定義についてみていきます。2次元平面上にベクトルaとベクトルbがあるとき2つのベクトルの関係を内積として以下のように定義しています。

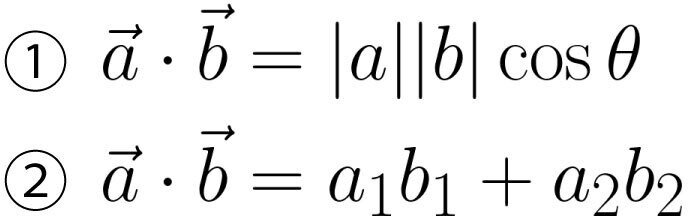
「もう見飽きたよ...」という方もいらっしゃるかと思いますし、ネットで内積を検索するとほとんどのサイトではまず最初に定義から解説が始まります。しかし、実はこの定義の関係こそが超重要だったりします。

この定義の①と②は余弦定理から相互に導くことが可能で、①と②は内積の定義から以下の通りとなります。

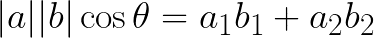
ここからが真骨頂です。ベクトル自体は大きさ(長さ)と向きをもつ量でした。そこで2つのベクトルの大きさを1として向きだけの要素のみで内積を考えてみると、|a|=|b|=1となり

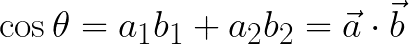
として表すことができます。つまり大きさ1の2つのベクトルで考えたとき、内積はcosθとして表すことができます。

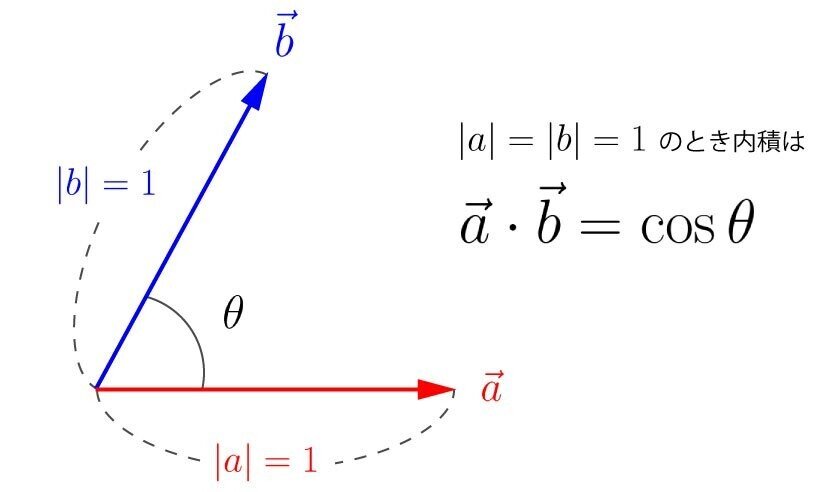
これを角度を求める式に変形すると次式が得られます。

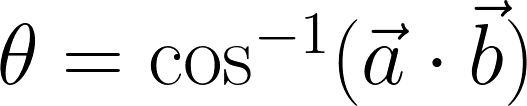
ここから分かることは、2つのベクトルが大きさ1の条件であれば内積はcosθとなってベクトル間の向きの関係(角度)が得られるということです。

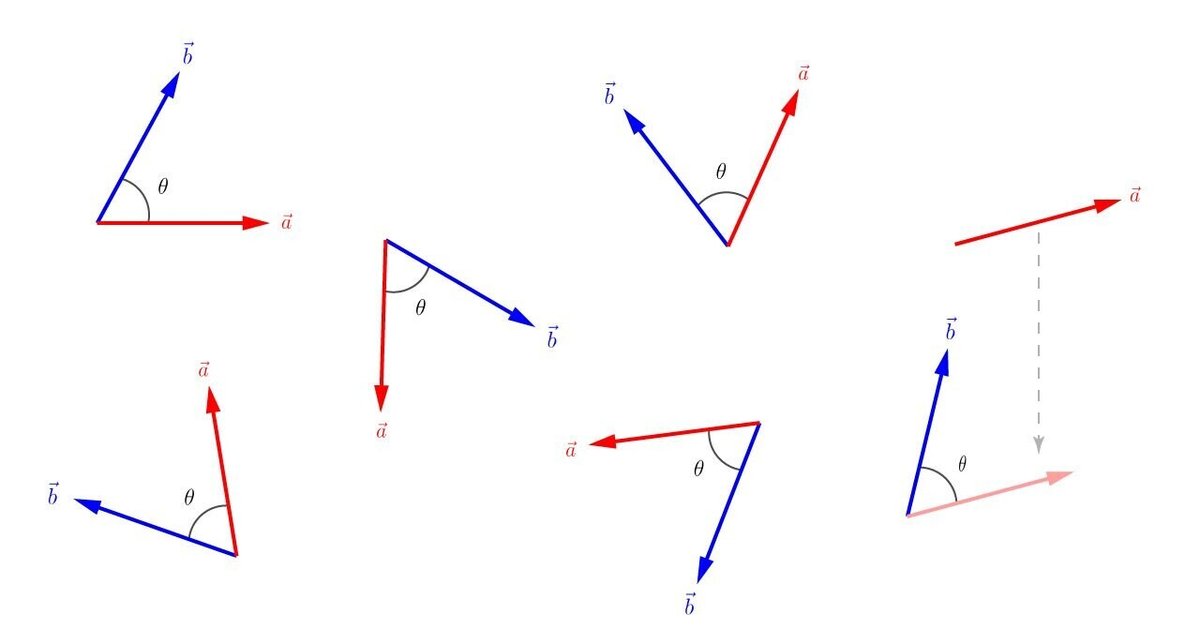
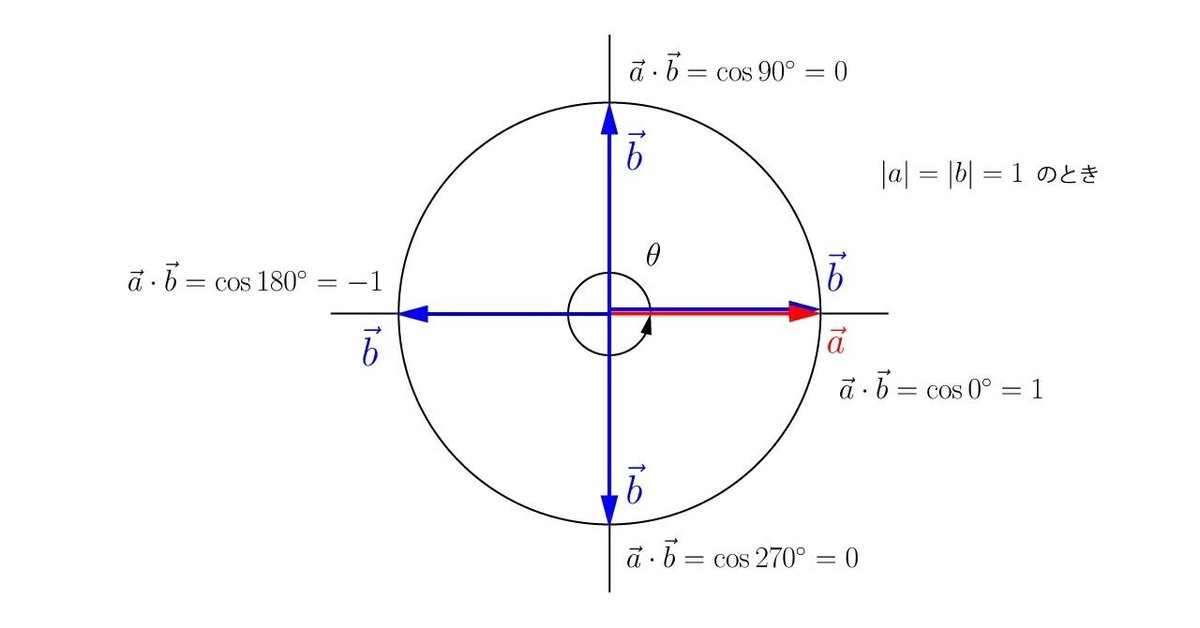
この関係が見えてくるだけでも内積が色々な場面で活用できそうな雰囲気を感じることができそうです。例えば

内積が
1のとき：2つのベクトルは同じ向き
0のとき：2つのベクトルの向きは直角
-1のとき：2つのベクトルは逆向き

ということが分かります。とは言え「ベクトルの大きさが1じゃないとダメなんじゃないの？」と思うかもしれません。でも大丈夫です。ベクトルには向きは同じで大きさ1の単位ベクトルを求める方法があります。

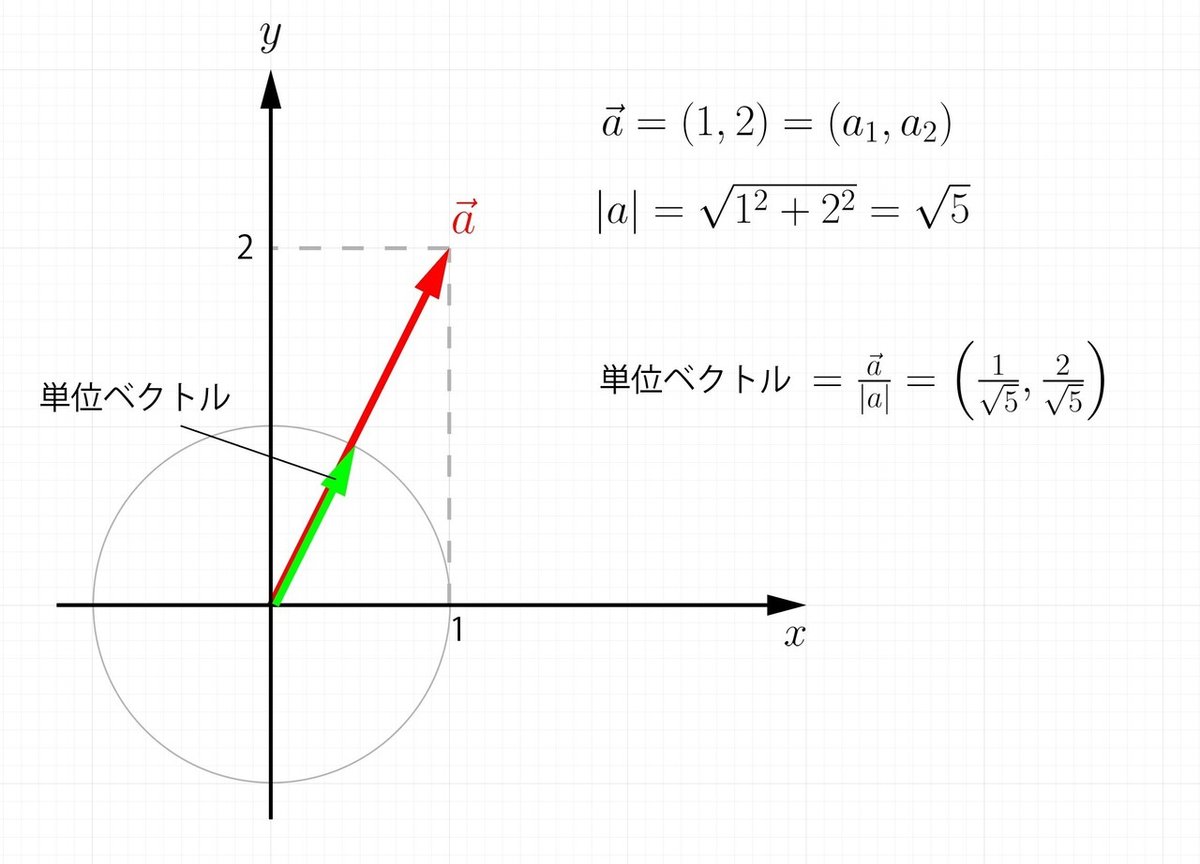
2つの対象のベクトルに対してそれぞれ単位ベクトルを計算し、内積という演算を行うことでどのような大きさのベクトル同士でも向きの関係を得ることができるようになります。まとめると

1. 2つのベクトルの単位ベクトルを求める
2. 内積の定義式②を使って内積を求める
3. 得られた内積と定義式①を組み合わせてベクトル間の角度を求める

という流れになります。このことから、内積には2つのベクトルの向きの関係性が数値(スカラー)として含まれていることが感じ取れるかと思います。

サイトによっては内積をベクトルの射影を用いて視覚化することで理解を促す手法も見受けられますが、内積の実体を見て無理やり理解するよりも定義の関係性を知ることで内積のイメージが掴みやすくなるかも知れません。

ここで考え方が掴めたら、今度は実際にUnityを使った内積の活用方法を見ていきましょう。

Unityで内積を活用する：視野角編

内積を使うと2つのベクトル間の向きの関係性を知ることができるようになりました。そこで、3Dゲームを想定したときにプレイヤーの視界にターゲットが入ったら何らかの処理をすることについて考えてみます。

まずプレイヤーには視線(カメラ)の向きというベクトルが存在します。どっちの方向を向いているかということですね。次にプレイヤーの位置を基準としたターゲットの位置というベクトルも存在します(ターゲットがどちらの方向にいるか)。まとめると以下の図のようになります。

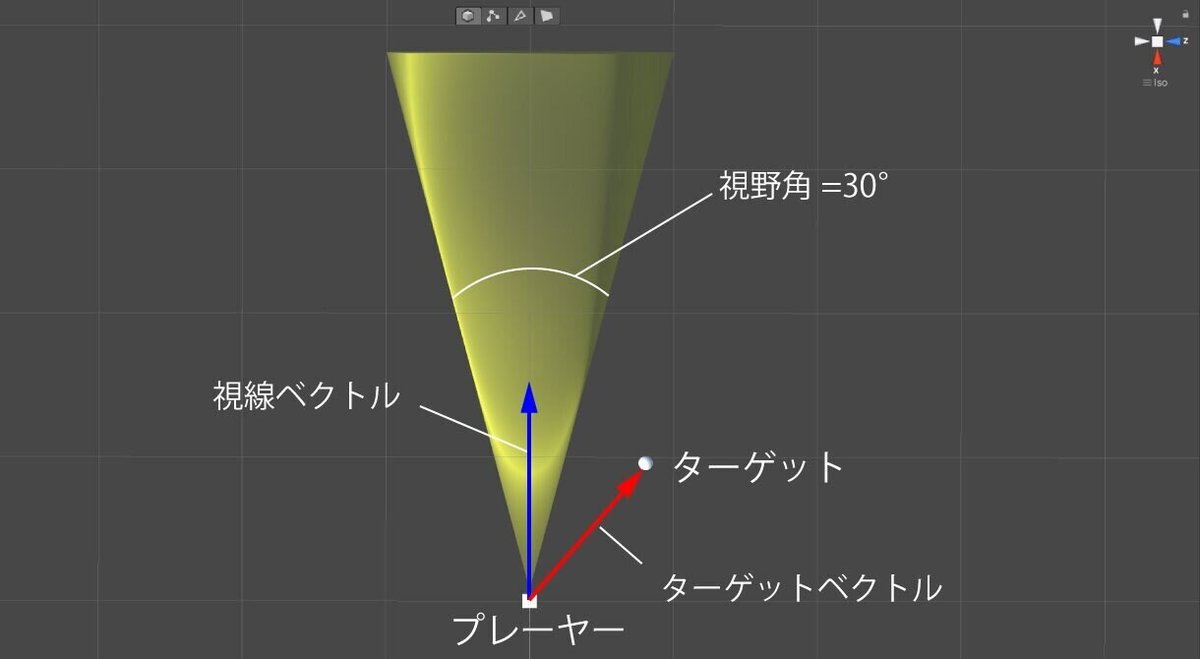
今回はプレーヤーの視野角を30°と設定しました。ではそれぞれのベクトルについてみていきます。Unityの場合、視線の向き(ベクトル)はカメラオブジェクトから

camera.transform.forward;

で得られます。ここで得られるベクトルはノーマライズされており、単位ベクトルとして扱うことができます。

プレイヤーの位置を基準としたターゲットの位置ベクトルは、ターゲットの座標からプレイヤー(=カメラ)の座標を引き算します。

(target.transform.position - camera.transform.position).normalized;

引き算の括弧の外にあるnormalizedはターゲットの位置ベクトルをノーマライズして単位ベクトルとして返してくれるメソッドです。Vector型(Vector3など)に備わっている機能でコードを書かなくても簡単に単位ベクトルが得られるため、ベクトル操作を行うときは積極的に使っていきましょう。

得られた2つの単位ベクトルから内積を求めます。定義②の式を使って自力で求めることも可能ですが、UnityにはVector3.Dot(a, b)という内積を求める関数が備わっているのでこれを使います。

var dot = Vector3.Dot(
   camera.transform.forward,
   (target.transform.position - camera.transform.position).normalized
);

dotにはcosの値が入っているので、アークコサイン関数とラジアン角度変換を使って角度を求めます。

var deg = Mathf.Acos(dot) * Mathf.Rad2Deg;

最後に得られた角度(deg)が設定した視野角内に入っているかを判定します。今回は30°と設定したので中心を基準として角度が15°(上下左右で30°)以下になったとき視野角に入ったとして処理します。

if (deg <= 15) {
   // 視野角に入った処理
}

全体のコードは以下の通りです。

using UnityEngine;
using UnityEngine.UI;

public class Controller : MonoBehaviour
{
   [SerializeField] Camera cam = default;
   [SerializeField] GameObject target = default;
   [SerializeField] Material red = default;
   [SerializeField] Material white = default;
   [SerializeField] Text debugText = default;
   private MeshRenderer targetMesh = default;

   void Start() {
       targetMesh = target.GetComponent<MeshRenderer>();
   }


   void Update() {
       var dot = Vector3.Dot(
           cam.transform.forward,
           (target.transform.position - cam.transform.position).normalized
       );

       var deg = Mathf.Acos(dot) * Mathf.Rad2Deg;
       debugText.text = deg.ToString("F0") + "°";

       if (deg <= 15) {
           targetMesh.material = red;
       } else {
           targetMesh.material = white;
       }
   }
}

上記のコードを適当なオブジェクトにアタッチし、インスペクタ上で必要なオブジェクトを設定して動作させると以下のようになります。この例では設定した視野角(30°)以内にSphereが入るとマテリアルを変更して色が変わるようにしています。

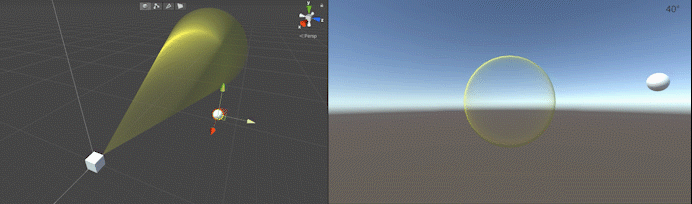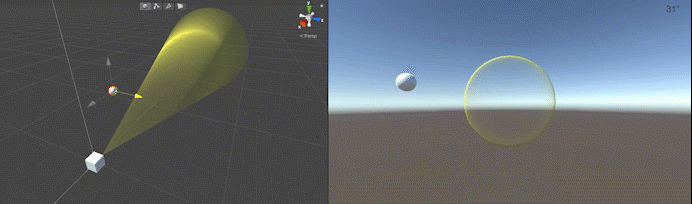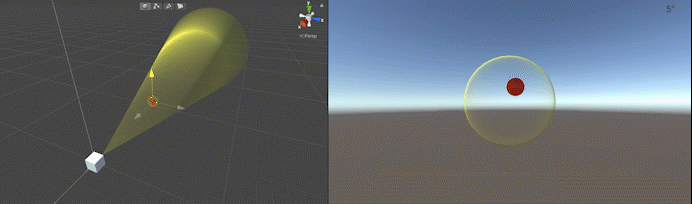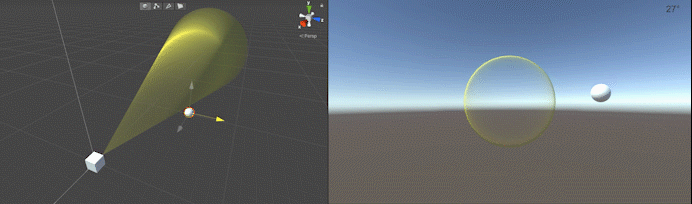
解説に使用したコードはGitHubで公開しています。

GitHub - takahiroyasui/DotProduct01

Unityで内積を活用する：シェーダー編

もう一つの内積の活用例として、シェーダーを用いたオブジェクトの透明化をご紹介します。法線を使ったお馴染みのアレです。

まず初めに検証用モデルを用意します。CubeやSphereでも問題ありませんが、分かりやすいように今回はStanford Bunnyを使います。Stanford Bunnyは以下のサイトからobjファイルをダウンロードすることができます。

McGuire Computer Graphics Archive

ダウンロードが完了したらobjファイルをUnityエディタ上のProjectパネルにドラッグアンドドロップします。モデルを取り込んだらヒエラルキーに配置して見やすい位置にセットします。

次にProjectパネルを右クリックし、[Create] > [Shader] > [Unlit Shader]を選択します。ファイル名は任意で構いません。ここではSampleとします。

作成したシェーダーを選択した状態で右クリックし、[Create] > [Material]を選択してマテリアルを作成します。シェーダーを選択した状態で作成することでマテリアルにシェーダーを紐づけた状態で作成することができます。

シェーダーをダブルクリックしてファイルを開き、以下のコードを貼り付けます。

Shader "Sample"
{
   Properties {
       _Color ("Color", Color) = (1, 1, 1, 1)
  }

	SubShader {
		Tags { "Queue"="Transparent" }
		LOD 200
		
		CGPROGRAM
		#pragma surface surf Standard alpha:fade
		#pragma target 3.0

		struct Input {
			float3 worldNormal;
     		float3 viewDir;
		};

       fixed4 _Color;

		void surf (Input IN, inout SurfaceOutputStandard o) {
			o.Albedo = _Color;
			float alpha = 1 - (abs(dot(IN.viewDir, IN.worldNormal)));
    		o.Alpha =  alpha;
		}
		ENDCG
	}
	FallBack "Diffuse"
}

ここでは内積に関する部分のみ解説します。シェーダーコードの以下の部分に注目してください。

float alpha = 1 - (abs(dot(IN.viewDir, IN.worldNormal)));

この行でアルファ値を代入しています。右辺の計算式では

dot(IN.viewDir, IN.worldNormal)

という演算を行っています。dot(a, b)は内積を行う関数でIN.viewDirでカメラの視線ベクトル、IN.worldNormalはオブジェクトの法線ベクトルを代入しています。それぞれのベクトルは大きさ1の単位ベクトルです。イメージとしては以下のようになります。

オブジェクトの法線ベクトルはオブジェクトの中央では視線ベクトル(カメラ)に対し平行になりやすく、中央から離れるほど直角になる傾向があります。

つまり、視線ベクトルと法線ベクトルの内積を取って平行な場合はアルファ値を大きく、直角にいくほどアルファ値を小さくするように処理すれば輪郭がはっきりとした透明感を持ったガラスのような質感を表現することができます。

内積を計算したあとabs()として絶対値を取っているのは、視線ベクトルと平行ではあるものの逆方向ベクトルの場合、負の値になるため必ず0~1の値になるようにしています。

アルファ値は0~1の範囲で0で透明、1で不透明として扱われます。そこで平行ほど内積(=cosθ)の絶対値は1に近づくため、これに伴ってアルファが減少するように最後に1から計算結果を引き算しています。

前置きが長くなりましたが、シェーダーを保存してマテリアルをStanford BunnyのMesh RendererのMaterialsに設定します。

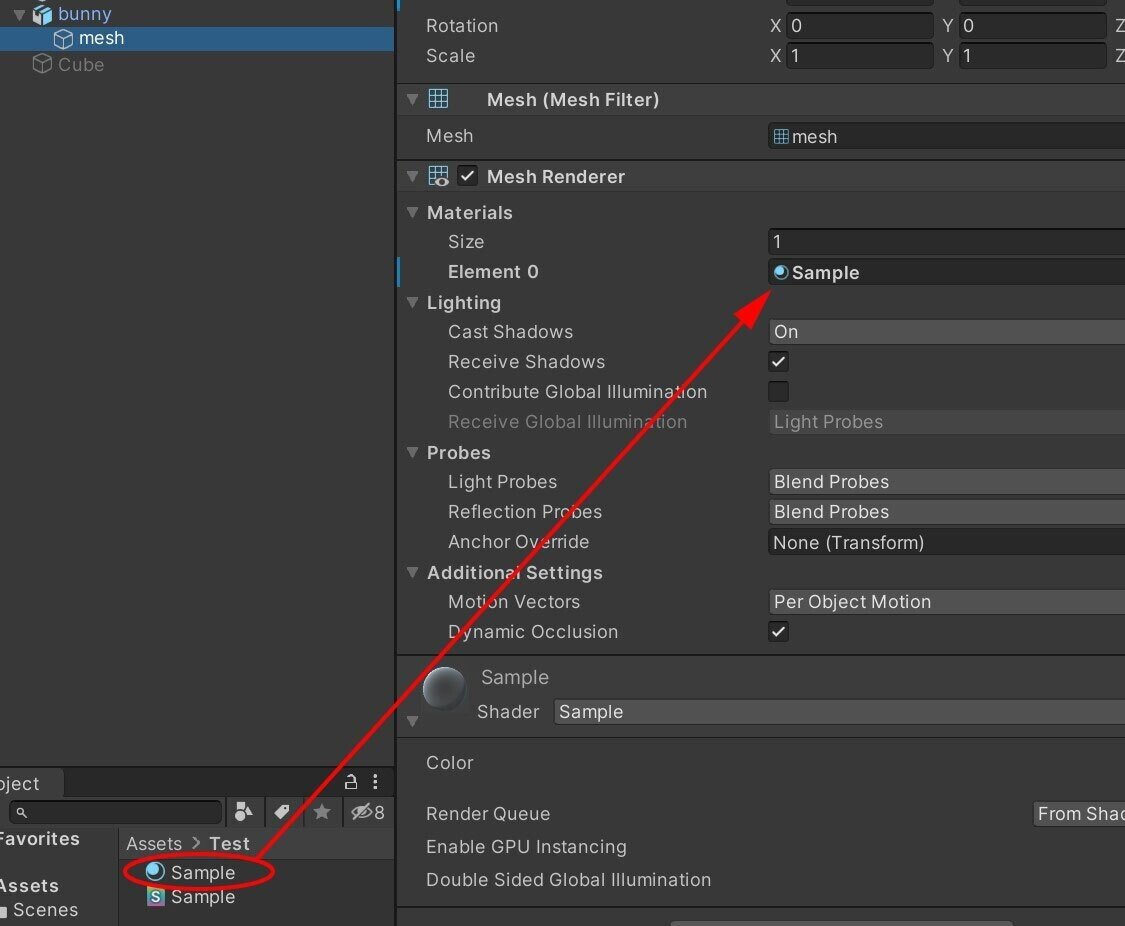
Sceneビューで確認するとオブジェクトがガラスのような質感に変わっていることが分かります。

おわりに

最初に考え方として内積は定義の関係性を知ることでイメージが掴めるように解説しました。そのうえでゲームエンジンのUnityを使って内積がどのように活用できるかを知ることで、内積のもつパワーを実感していただけたと思います。

内積を扱えるようになると、オブジェクト座標空間制御やライティングなどの光の制御が可能となり表現の幅を大きく広げることができます。是非、内積を使いこなして創作活動に活かしていただければ幸いです。🌱

参考

内積とは何なのか？ベクトルの内積の2つの求め方とその活用法｜アタリマエ！

内積について非常に分かりやすいサイトです。ここを読むだけでも内積を理解できると思います。

【Unityシェーダ入門】氷のような半透明シェーダを作る - おもちゃラボ

シェーダーといえば「おもちゃラボ」さん。半透明シェーダーの内容はほぼこのサイトを参考にしています。