
同じ誕生日のクラスメートがいる確率⭐️計算してみた⭐️
皆さん、こんにちは!!
今日は水曜日です!!
ひこまるは、実験系の研究室なのですが、コロナの影響で実験をできる日数に制限があります。
水曜日は実験できる日!!
めっちゃ楽しい!!
すごい成果出すぞ!☺️
突然ですが、私の研究室では、みんな誕生日の月が違います。
研究室の中で、誰かが誕生日の時はケーキ買ってきて食べたりするので、
バラけているのは嬉しいです!
(今はコロナのため、もちろん行っっていません。)
皆さんは自分と同じ誕生日の人と会ったことがありますか??
同じ誕生日なだけで、テンション上がりますよね。
365日もある中で、一致するなんてキセキです!!⭐️
しかし、それは本当に珍しいことなのでしょうか??
実際にどの程度の確率で同じ誕生日の人がいるのかでしょうか?
疑問を解決するために、実際に計算してみました!
こんな人におすすめ
・数学が好きな人
・数学に興味が持てない人
・同じ誕生日の人がどの程度いるのか気になる人
今回の記事の簡単なまとめです。
✅40人のクラスでは、89%の確率で同じ誕生日の人がいる
✅40人のクラスでは、10%の確率で自分と同じ誕生日の人がいる
✅日本人の誕生日には偏りがある
この記事を読んで、
「数学を理解すると、自分でいろんなことが計算できるのか」と感じていただければ嬉しいです!☺️
今日もよろしくお願いします!
同じ誕生日の人がいる確率⭐️計算してみた⭐️
⭐️必要なもの⭐️
・紙
・ペン
さて、実際に計算をやってみましょう!
⚠️注意⚠️
ここでは、簡単のため、同じ誕生日のクラスメイトがいない場合の確率を、まず計算します!
いない場合を計算することができれば、その数値を用いて、いる場合の確率はすぐに求めることができます。
(いない場合の確率が簡単なのかについては、この章の最後で説明します。)
クラスの人数は、40人としますが、
まずは2人、3人、4人の場合に異なる誕生日の確率を計算して、雰囲気を掴んでみましょう。
最初に生徒が2人の場合について考えてみます。
1人目の誕生日と2人目の誕生日が異なる確率は、

となります。
これは、2人目の誕生日は365日の中で1人目の誕生日以外の364日のどれでも良いので、このような確率になります。
これは、パーセント表示に直すと約99.7%となります。
つまり、クラスメイトが2人の場合、その2人の誕生日が異なる可能性は99.7%です。
ほとんど、一致しないことがわかりました。
では3人の時は、どうでしょう。
2人目は、1人目と違う誕生日であればよくて、
3人目は1人目とも2人目とも異なる誕生日であれば良いです。
つまり、式にすると、
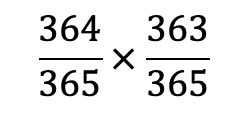
となります。
これをパーセント表示すると約99.2%です。
まだまだ、同じ誕生日の人は出てきそうにありません。
同様に4人の時は、
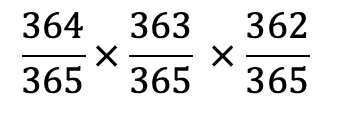
となり、これは約98.4%です。
なんとなく、流れは掴めていただけたと思います!
それでは、本番です!
次は40人のクラスで計算してみましょう!
40人の場合、次のように計算をすれば確率を求めることができます。
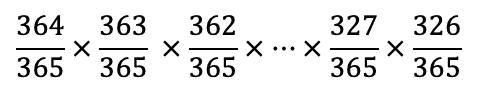
これを実際に計算すると、

約0.109です。
パーセント表示では、10.9%となります。
これが、40人の誕生日が異なる確率です。
全体100%から、40人全員の誕生日が異なる確率10.9%を引けば、同じ誕生日の人がいる確率が求まります。
40人のクラスでは、同じ誕生日の人がいる確率は、
89.1%という結果がわかりました!
(100 - 10.9 = 89.1)
40人のクラスであれば、その中で同じ誕生日の人がいても当たり前なんですね。
⭐️補足:何故、誕生日が異なる確率を計算したのか
補足なので、興味がない方は読み飛ばしていただいて構いません。
何故、同じ誕生日の人がいる確率ではなく、クラスの中に同じ誕生日の人がいない確率を計算したのか。
その答えは、同じ誕生日の人がいる確率は非常に複雑な計算が必要だからです。
ここでは、簡単にクラスの人数が4人の時を例にあげます。
上で、4人の時、全員の誕生日が異なる確率は98.4%と簡単に計算ができました。
つまり、同じ誕生日の人がいる確率は、1.6%ほどです。
これを、最初から同じ誕生日の人がいる確率を求めるようと考えると、場合わけが必要になります。
誕生日が同じ人が2人だった場合、3人が同じだった場合、4人とも同じだった場合、2人が同じ誕生日であって、それが2組だった場合などなど、非常に計算が複雑になります。
やりたくなかったので、誕生日が異なる場合を計算しました。
直感とのズレ
皆さんは、先ほどの章の結果をご覧になられてどう感じましたか?
多くの方にとって驚きの数字だったのではないでしょうか?
89%の確率で同じ誕生日の人がいる??
今まで自分と同じ誕生日の人なんてあったことないけど、本当に計算あってるの??
このように、疑問を感じた人も多いと思います。
そのような、直感とのズレは何故起こるのでしょうか?
数学が間違っているのでしょうか?
これは、私の推測ですが、
同じ誕生日の人がいる確率 ≒ 自分と同じ誕生日の人がいる確率
と考えているためではないでしょうか?
上の章での計算は、同じクラスの中で誕生日が一緒の人がいる確率です。
それでは、自分と同じ誕生日の人がいる確率も40人のクラスで計算してみましょう!
自分と同じ誕生日の人がいる確率⭐️計算してみた
では、自分と同じ誕生日の人がいる確率についての計算を短めにまとめてみました。
今回も、自分と異なる誕生日の確率を計算して、それを全体100%から引いて求めます。
では、39人(40人のクラスから自分を抜いた数)が全員自分と違う誕生日だとすると、
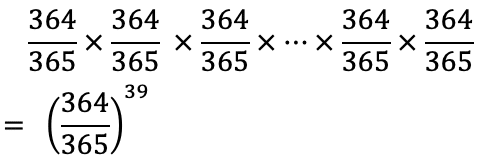
このような計算をすることで求まります。
計算の結果、約89.9%になりました。
つまり、自分と同じ誕生日の人がいる確率は全体100%から上の数字を引いて
約10.1%とわかりました。
つまり、同じ誕生日の人がいる確率でも、自分という制限をつけるだけで、約10%しかいなくなるのです。
ここまでのまとめ
40人のクラスの中で誕生日が同じ人の確率は89%だが、
自分と同じ誕生日の人がいる確率は僅か10%程度である。
日本人の誕生日には偏りがある
最後にちょっとした雑学をお話しして終わりにしようと思います。
実は、日本人の誕生日には偏りがあることをご存知ですか?
これは、週刊女性が厚生労働省の人口動態調査をもとに出生に関するデータを10年分リサーチした誕生日多いランキングです。
左は、多い誕生日で、右は少ない日です。
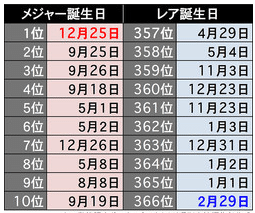
(人口動態調査('95年〜'14年)より週刊女性編集部作成)
このデータによると、1位の 12/25 は、7万1183人が生まれているにも関わらず、365位の 1/1 は4万3006人と、倍近い差があることがわかりました。
年末年始が少ないことは、医師との相談で出産日を変える人がいることが原因と考えられています。
例えば帝王切開などを行う場合、医師の少ない年末年始や土日祝日は選ばないことが多いです。
逆に、記念としてクリスマスに調整したり、(クリスマスから妊娠期間280日前後の)9月20日前後が多いことなども傾向としてわかるようです。
まとめ
いかがでしたでしょうか?
「クラス内に同じ人がいるのか、自分と同じ人がいるのか」だけでここまで大きな差になることはなかなか驚くことかもしれません。
確率を正しく理解することによって、自分たちの身近なことについて知ることができます。
今後もこのようなコラムを上げていきますので、ぜひよろしくお願いします。
では、また次の記事で!
参考HP
