音楽の拍節とフレーズ —時間構造の認知理論—(2)
第2部 フレーズの構造とその構成法
第5章 拍節構造を用いたフレーズ構造の理解
第1節 フレーズとは何か
大雑把な理解
人はある対象を、適度に大雑把に理解することができる。 例えば遠くにいる犬を、その犬種は特定できないかもしれないが、とりあえず犬として理解できるであろうし、大抵の会話においてはその程度の理解で十分である。もしも犬に関する会話に、犬種や年齢、体長、体重、その他の詳細な情報が常に必要不可欠であるとされたら、よほどその犬についての知識を持たない限り人は何が言われているのか識別することもできないであろう。詳しい知識を持たなくてもその話題が犬であると把握できるのは、大雑把な理解のおかげである。別の例を挙げれば、人は三角形について、話題となっている図形の3つの辺の長さや角度を正確に知らなくても、三角形について語ったり聞いたりすることができるであろう。
同じことが音楽においても成立していると考えることができる。例えば12拍子は大雑把に4拍子として理解できる。これはさらに大雑把に2拍子として、あるいはさらに1つの大きなビートとしても理解することができる。このような理解の仕方は、テンポの速い楽曲では自然と行われている。もちろんテンポを緩やかにしていけば、その逆が成り立つ。
こうした大雑把な理解は、その際に用いるスキーマを、より抽象的なスーパースキーマに遡らせることによって行われていると考えられる。12拍子は認知的に4拍子の1種である。つまり、12拍子を理解するためのスキーマは、4拍子のためのスキーマを細分化したものであり4拍子の性質を継承している。同様に4拍子は2拍子の性質を継承しているし、2拍子は1つの小節あるいは1つのビートとしての性質を継承している。
ところで2拍子の楽曲において、フレーズやグループが様々な形を取るのにも関わらず、それらが2拍子であり続けるのはなぜだろう?上で述べたことを敷衍すれば、それらのフレーズのスーパースキーマが2拍子だからであると言えるのではないだろうか?これは本論第2部の基本となるアイデアであり、それは拍節とグループを別々の構造と捉えるGTTM理論などの理論と本理論を分かつ極めて重大な特徴である。
第4章では、拍節的概念の範囲内で、このように拍節のスキーマ・システムがそれぞれの拍子のスキーマを生成する仕組みを説明した。この際、分割して得られる下位のスキーマは、上位のスキーマの支配する範囲を越えることは決してない。小節をどのような分割の仕方で細分化しようと、下位区分のカバーする範囲は必ず小節の範囲内に留まっている。このような制限を通常の拍節構造の1つの特徴とみなすことができる。
ところですでに本論では、スキーマとグループの関係について論じている。音は自らグループになることはなく、聴き手があるスキーマを適用することによってそれらの音はグループとなる。よって音のグループは必ず、それらの音をグループにしているスキーマに基づかねばならない。これを私は「グループ化の原理」と呼んだ。だから本論の第1部で展開された理論の範囲では、小節や拍といった拍節単位に一致するようなグループしか扱うことができない。だが、音楽におけるグループは拍節構造より多様である。
よって、より多くのグループについて説明できるためには、拍節スキーマを拡張していかねばならないことになる。第2部では、音楽におけるグループを一般的に扱うために2段階の進め方を取る。第5章では、スキーマを拍節的なもののままにし、そこからの逸脱した部分を一種の装飾として処理する。第6章では、そのような逸脱をより詳細に表現するために、拍節スキーマが装飾的に拡張される。
フレーズの定義
(※補足:フレーズを以下のように定義することは理論全体からすると不必要なことであったかもしれない。フレーズとグルーピングを同じ意味だと考えても大きな違いはないが、最も意識されるレベルのグルーピングというものが、ここで言われるフレーズのことだと思っていただきたい。)
本論では拍節スキーマとグループを対応付けているので、グループは階層的な概念である。だが、我々の常識的な音楽経験においては、どのレベルの階層でもグループが同じように振る舞うというわけではない。ある特別なレベルではグループは、1つの滑らかな音の連なりとして理解され、その両端には強さの差はあれど切れ目が感じられる。つまり、階層的なグループ構造のうちのいずれかのレベルが「輪郭的」に感じられる。そのレベルより大きなレベルでのグループは、そのような音の連なりが幾つか連続した集まりなのであって、全体が1つの音の連なりとして理解されるのではない。もしもそのグループ全体が1つの音の連なりであるならば、それが特別のレベルになるだろう。逆に、より小さなレベルでは、グループ同士の間に音の切れ目を作ることができない。もしも切れ目を作ればそれぞれが特別のレベルのグループになるであろうからだ。すなわち、このような特別なグループは階層的な性質を持たず、その都度いずれかのレベルのグループがこのような特別なグループとなる。ただし、上下に隣り合ったレベルのどちらが特別なグループとなるのかについて曖昧さが生じることはある。
本論では、このような特別なグループが、音楽家が「フレージング」(phrasing)と言う場合の「フレーズ」に当たるものであると考える。それは、この特別なグループこそが、音楽を理解する際に聴き手が最も具体的な音楽的構造として感じるものに対応すると考えられるからだ。
このようなフレーズが連続して大きなグループを作るとき、そのやり方を「フレーズ構成」呼ぶことができるだろう。そして、拍節的な階層性の理解まで含めて構造をとらえるとき、「フレーズ構造」という言葉を使うことができる。このようにフレーズを定義すれば、実践において「フレージング」という言葉が用いられる際に対象としているものに近い概念になる。
このような定義の仕方は、分析者の恣意性を許してしまうという点で問題があると思われるかもしれない。だが、実際のところ、このような人の認知的な選択に依存するような特別なグループがどこにどのように存在するかを決定する客観的で一般的な方法は簡単には作れない。無理矢理何らかの方法を決めたところで、対象を捉え損なってしまっては意味がない。本論もまた、そのような決定のための方法を提示することを目的としていない。しかし、客観的に決定する良い方法がないとしても、聴き手は確かにその都度、どこかのレベルにそのような具体的な輪郭を持つ対象を認めている。誰かがフレーズがそこにあると判断する際に、その構造を説明できるような理論であればここでは十分であろう。このような定義は一見曖昧に思えるが、そもそもフレーズ自体が聴き手の認知的選択に大きく依存する曖昧な対象なのだとすれば、このような定義の方がむしろ対象を正しく捉えている。今後の研究によっては、人間の判断を仰がなくてもどこにフレーズが感じられるかを判断できる理論が作れるかもしれないが、それは本研究で必要な条件ではない。本研究では、できる限り多くの人の解釈が一致するような例だけを取り上げるように努めたが、それでも異なった解釈が不可能なわけではない。しかし何度も言うように、この理論は正しい解釈を決定するための判定基準を与える理論ではないのだから、異なった解釈が可能なことは、理論に対する反例にはならないということだけはあらかじめ注意しておきたいと思う。言語における文の切れ目などとは異なり、音楽においては、フレーズの区分に複数の解釈が成り立ちうることが当たり前であり、そのような曖昧さを許すような理論でなければむしろ正確に対象を捉える理論とは言えない。
フレーズを見出す1つの簡単な目安は、大抵の場合、作曲家が歌詞の1行を当てはめるのが1つのフレーズだということである。これは、作曲家がこの範囲を1つの特別なレベルのグループとして認めていることの証拠である。なぜならば作曲家は、聴き手にとって歌詞が容易に理解できるようにするために、1つの詩行を音楽的に1つのまとまりと感じられるようにするし、詩行の終わりは切れ目をはっきり分かるようにしようとするからである。なおこれは、作曲家が歌詞に合わせて曲を作ったり、曲に合わせて歌詞を乗せる、という意味であって、歌詞の存在が音の連続に区切りを生じさせるというふうに、刺激が人間の外部で相互作用するような意味には捉えないようにしていただきたい。基本的に歌曲は、多くの場合で歌詞が無くても歌曲のフレーズがある程度はっきりと区分できるように作られている。歌詞の影響によって境界が変化する場合も、そうした区分を行うのはあくまでも人間である。
譜例5-1.1はモーツァルトの歌曲からの例であるが、歌詞のそれぞれの行が、その内容に見事に一致するそれぞれ1つの音楽的フレーズによって表現されていることが分かるだろう。本研究では譜例においてフレーズの繋がりを破線のスラーによって表示する。また、譜例が見にくくなることを避けるために、基本的に楽譜は小節線と音の配置以外の記号を省略して示すことにする。

しかし詩行との対応も、あくまで目安に過ぎないということは言うまでもない。時に、詩行の途中でフレーズが区切れを持つこともあるし、複数の詩行を1つのフレーズに収めることも不可能ではない。それは作曲家の判断次第である。時に、表現手段として歌詞の区分とフレーズの区分がずらされることもあるだろうし、別の場合には作曲家が無頓着なために不一致が生じている場合もありうる。しかし表現手段として意図的にずらすということは決して多くないし、著名な作品を扱う限りにおいては作曲家の失敗を考える必要はほとんどないので、詩行との対応がかなり有効な目安であることは間違いない。
ただし、1つのフレーズと同等のグループが、細かい複数のフレーズによって形成されている場合というものがあるので注意が必要である。第6章で扱う斜拍子という形は、フレーズの音のまとまりが細分化しやすい形である。譜例6-1.5の『もう飛ぶまいぞこの蝶々』はそうした例である。
和声的にフレーズが定義される場合もある。その場合、カデンツ、つまり和声的な終止形がフレーズの区切りとして用いられる。だがこれには大きな欠点がある。それは、このやり方では、和声的な終止形を伴わない区切りについて何ら説明することができないことである。これでは「フレージング」という言葉が含む意味を全くカバーできないであろう。なぜなら、通常フレージングが扱う対象は、和声的な終止によって区切られる範囲よりも細かいからである。だが和声は、通常認められる和声的な終止形よりも軽い区切りを語る手段を与えてくれない。
実のところ和声的な終止形は、それが実際に終止する限りにおいては必ず「リズム的」にも終止であるが、必ずしも「リズム的」な終止が和声的な終止の定型を伴うとは限らない。和声進行はリズム的要素の助けを借りなければ存在できないが、終止自体は特別の和声進行が無くても生じうる。すなわち和声は、リズム的な終止形に和声的な機能を付与するのであって、終止する機能それ自体はリズム的に与えられると考える必要がある。
和声によって捉えるやり方に対して、音楽の時間構造から捉えるやり方を、ここでは通俗的な用法に従って「リズム的」と呼んだが、今日「リズム」という用語はあまりにも多義的となっており、理論的な議論のためには不向きである。本論の考え方では、ここで「リズム的」な終止、と呼んだものは、拍節的なグループの「まとまる作用」と、フレーズという特定のレベルのグループが「最もはっきりと輪郭的に捉えられる、という作用」に由来するものである。
和声的な終止形に頼る事ができないことを事例によって説明しよう。次の例はF.シューベルトのリート『野ばら』である。mm.1–4に対して、m.5からの部分が同じ形で始まるので、「対句」としての理解が成立し、何らかの区分が生じる。そして確かにm.3–4にはV7-Iの終止がある。また、m.8は偽終止によってVIの和音で終わるが、m.10が改めて終止をやり直してトニックのIの和音で終わるので、mm.5–10までが2つ目の大きなグループであると言っていいだろう。ここまでは、終止形が大きな区分の終わりの位置にあるように思える。ところが、mm.11–12はどうだろう?和声はmm.3–4と共通である。
しかしmm.3–4の和声進行がmm.1–4の4小節の終わりを作っていたのに対して、mm.11–12にはそのような終わりの感覚が伴わない。どうしても、次の2つの小節mm.13–14と一緒にならないと安定した終わりを形成するように感じられない。mm.11–12が安定した終わりを作る能力を持たないとすれば、同じ和声進行であるmm.3–4に終止する力を与えているものが和声であるとは言えない。

次の譜例5-1.3では、和声的な終止形が8小節全体で1つしかなく、また冒頭の4小節が同じ和音である。和声はこの部分の「フレージング」を論じる何の役にも立たない。

また、和声的な終止形があれば必ずフレーズの区切りとなるというわけでもない。例えば、終止形の終わりの和音が、新しいフレーズの開始となるなどして、区切りがなくなってしまう場合である。このような場合に終止形を無理やり区切りとして理解しようとすると、後続するフレーズの先頭部分を強引に削り取るようなおかしな解釈となってしまう。
以上のような理由から、本論の研究対象を、和声によって定義することは不適切であると考える。和声によってフレーズを定義するとしても、それは「フレージング」という言葉が使われるのとは別の文脈で使われるべきものであろう。
フレーズの内側と外側の構造と用語について
構造に関する用語は、できるだけフレーズの内側と外側で共通の用語を使うべきであろう。これは、フレーズがどのレベルに存在するかが曖昧なのに、内と外で異なった用語を使うと、同じものが解釈の違いで別の名称で呼ばれることになり混乱するからである。よって、拍節スキーマやグループ、といったものは共通のものとして用いることになる。これらはどのレベルにフレーズがあろうと同じ意味である。
他方、区別すべきなのはフレーズの内と外で性質の大きく異なる事象である。フレーズの内部で最も特徴的なことは、音が繋がって感じられるということであるから、内と外とで区別すべきことのほとんどはこの性質に関係している。
ただし実際のところ、構造に関するほとんどのことはフレーズの内と外で階層的に共通である。また、フレーズの内と外で性質の異なる事象はより感覚的な曖昧なものであるので、本研究で優先すべきことがらではない。よって、基本的には階層的な説明を行い、フレーズの内外で違ってくることについてその都度注意を与えるというのが賢明なやり方であろう。
第2節 フレーズの基本構造
拍節的スキーマとフレーズの基本的な関係
さて、ではフレーズを作っていくことにしよう。まず単純な拍節スキーマを考える。次の図5-2.1のような、ある拍節単位を2等分する単純な拍節構造を考えることにしよう。

このようにして得られた2つの枠は、ミンスキーの言い方を借りるならば音楽的なイベントがアサインされるそれぞれのスロットである。ここではそれぞれに全音符がアサインされるものと考えよう。すると次の図5-2.2のような2音の音列が得られる。これは音高については未確定であるが、時間構造としては確定しており、抽象度を残した一種のインスタンスを生成したということになる。これを逆に捉えるならば、ある2つの独立した音の刺激を、2つの全音符の連続とみなしてこのスキーマによって把握するというふうに考えてもよい。すなわちこのスキーマは、音楽の理解(情報の入力)においても、音楽の製作(情報の出力)においても用いられるということである。
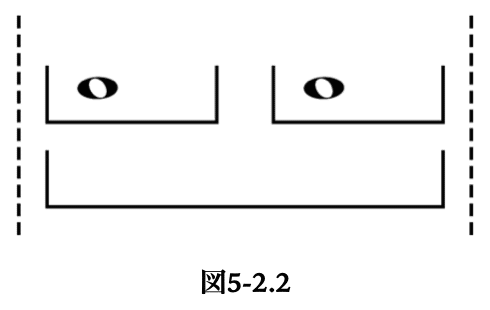
アサインされた2つのイベントは、拍節的スキーマに従った拍節的な結合力に対応する結びつきを持つことになる。見方を変えれば、聴き手がこの2つの全音符をこのようなスキーマに基づいて理解するとき、両者の間に拍節的な結合力が感じられるようになるということだ。グループがスキーマに基づくというのはこのようなことを意味している。聴き手はこのようにして、単なる音響的現象を音楽にする。すなわち、拍節的スキーマはフレーズ構造の音のグループを作る本質的な原因なのである。第3章ではこのことをグループ化の原理と呼んだ。
この章で論じることは、拍節的スキーマによって諸音がグループとして理解される仕組みである。そしてこの章で理解しうるグループ構造は、第4章で論じた拍節構造の範囲までである。よって、この第5章ではグループは、スキーマによって理解される骨格部分と、その骨格に付随する装飾的部分とに分かれることになる。次の第6章では、この骨格の構造を拡張して、装飾的部分をスキーマによって理解する方法を論じる。
リュシー標準形とリュシーアーチ
さてこのようにして、最も単純な拍節的スキーマによって、最も単純な2小節フレーズを構成することができた。イベントは開始の位置によって理解されるのだから、この2音の結合は、次の図5-2.3に矢印で示したような、2つの枠の先頭同士に架かる一種の建築物として感じられ、さらにこの全体は矢印の始点の位置によって代表されることになる。本論ではこの構造を最初に論じた人物にちなんで、この構造に基づくフレーズを「リュシー標準形(Lussy normal form)」によるフレーズと呼び、この拍節単位の結合を「リュシーアーチ(Lussy arch)」と呼ぶことにする。ただし、リュシーはこのようなアーチを、それぞれのフレーズが1つずつ持つものと考えていたが、本論ではこれを、グループの拍節的な結合力を表現するものとして階層的に用いる。よって後から論じるように、グループの階層性に応じて、リュシーアーチも階層的に考えることができる。

支配/従属関係としての結合
リュシーアーチの結合力は、一種の支配あるいは従属の関係として理解することができる。小節の中の拍は小節に従属するということは理解しやすいであろうが、さらにそれらの拍は、先頭の強拍にその小節内の後続の弱拍が従属しているものとして理解することができる。これは、先頭の強拍が、同時に上のレベルの拍節単位を代表しているからであり、また分割の出発点、つまり等時性スキーマの適用される起点となっているからである。拍節構造は、このような支配/従属関係の連なりであり、それがグループの階層性をもたらしている。フレーズはそうしたグループの1つの部分なので、フレーズのまとまりもまた、支配/従属関係に基づく結合の連なりである。
第5章での戦略は、フレーズの骨格をなす中心的な構造を、この拍節的な従属性に基づいて理解することである。その際この構造から逸脱する部分は、5章においてはこの構造に拍節的ではないやり方で従属するものとして理解される。次の第6章では、従属の別のあり方を導入することによってこの構造を拡張することになる。
リュシー標準形は、フレーズの構造の最も単純なモデルである。そして実践において極めて頻繁に利用される最も理解のしやすいフレーズのひな形である。リュシー標準形の本体は究極的には1つの拍節単位ということになるが、ただの1音では始まりと終わりの感覚を持ち得ず、フレーズとは認めがたいであろう。また、1音はすでに1つのまとまりであり、何かをグループ化したものではない。しかしここにアナクルーシスなどを付加した場合は、本体が1音でも独立したフレーズになりうるのだから、理論的には1音からでも、リュシー標準形の特別なタイプが形成されうるとしておくのがいいだろう。
スキーマを使ったフレーズの理解
この第2部では、最初はフレーズの大雑把な理解の仕方から始めて、徐々に細かい理解の違いの生じる可能性を見ていく。第3章で論じたように、スキーマはその詳細さを、必要に応じて調節できなくてはならない。なぜならば、詳しい理解が必要ない場合や、詳しく理解する余裕のない場合に、適度に細部の理解を捨てて大雑把な理解で済ませられるようにしなければならないからである。複雑なメロディーは、テンポが速い場合には詳しく理解している余裕が無くなり、拍子をとらえるだけで済まされるだろう。もっと速くなれば、小節を1つのビートとしたより大雑把な理解によって処理されるようになる。そのような場合に、テンポに関わらず詳細な理解を得ようとすれば処理は間に合わなくなるであろう。
譜例5-2.1は、リュシー標準形に適合する典型的なフレーズを2つ示した例である。これらのフレーズは、図5-2.3のような基本の形をスキーマとして作ったインスタンスとしてとらえることができる。ここでは大雑把な理解を考えているので、スキーマは粗い大雑把なものであり、小節の中の詳しい構造については無視されている。

小節の中の構造は、図5-2.3の基本のスキーマをより細分化したものによって理解されることになる。その典型的なものは、小節の中により小さいリュシー標準形が埋め込まれていると理解できるものである。本論はこのような細分化した理解を、拍節的スキーマを細分化しながら、第5章第3節の「ウメコミ」や、第6章でさらに詳しく論じることになる。
3小節のフレーズ
リュシーアーチは、3小節構造でも生じる。しかし3小節によるフレーズは、その内部構造にいくつかのタイプが考えられるために、2小節によるものより複雑になる。
第1のタイプは、第4章で論じたような不等分割拍子に対応する(2+1)の構成である。リュシーアーチは1つ目の小節の先頭から、3つ目の小節の先頭へと生じることになる(図5-2.4)。不等分割拍子の説明と同じように、この構造は、4小節のリュシー標準形(2小節+2小節)の最後の1小節を取り去ったものと同じ形である。


このような形が生じるパターンを網羅することはできないが、典型的な例としては次のような場合がある。4小節フレーズにおいて、3つ目の小節でメロディーが終わってしまった場合、4つ目の小節の開始する位置から次のフレーズを始めやすくなる。そのような時にしばしば3小節フレーズが生まれる。譜例5-2.3のような、強拍でメロディーが終わる形は特にそれが起こりやすい。

同様のことは表記上の小節に限定されるわけではない。拍節は階層的に同じ性質を持つのであるから、この形は、例えば2小節フレーズの場合にも起こるし、その場合フレーズは1.5小節の長さとなって、半小節ずれたフレーズが次に続くことになる。
次の譜例5-2.4では、m.11からのフレーズが1.5小節で終わるために、m.12の後半から半小節ずれたフレーズが始まっている。これがずれた形であることは、その次の譜例5-2.5のm.21–22に正規の位置で同じ形のフレーズが登場するから分かる。このズレが楽曲の演出上どのような効果を持つかはここでは論じないが、フレーズの骨格を成す拍節が小節線によって示されるとは限らないことははっきり分かるだろう。


シューベルトの『アヴェ・マリア』(エレンの歌第3番)(譜例5-2.6)も同様に、歌の最初のフレーズが1.5小節の長さであり、以後ずれて表記されたフレーズが続く。このズレは、第7小節後半から再び1.5小節のフレーズが出ることによって解消されている。

第2のタイプは(1+2)の構成で、これはシンコペーションを含む形である。この場合後半の2つの小節は小さなリュシーアーチを持ちうる。リュシーアーチの起点が、通常の拍節構造から得られない位置にあるということがシンコペーションの特徴である。シンコペーションの詳しい構造については第6章で論じるので、ここでは形の紹介に留める。
次の譜例を、第2のタイプになりうる例として挙げるが、これは(2+1)として解釈することも十分可能である。特にこの例の場合、初めの2小節は冒頭の主題と同形であるから、(2+1)の解釈がなされやすいだろう。その場合には、3つ目の小節が付加された形となり、これと元あった2小節との間にリュシーアーチが形成される。

次の『ライアー弾き』の前奏の8小節は、2小節の前置きと、(3+3)の主要部分とに分析できるだろう。その際、それぞれの3小節は、やはり、(2+1)の解釈も(1+2)の解釈も許すようなものになっている。消え入るようなエコーの効果を求めるのであれば、(2+1)の解釈がこの曲にはより相応しいように感じられる。その後で歌が始まってから、mm.11–12において問題となっている3小節フレーズの初めの2小節だけを出して終わっていることが、(2+1)の解釈を補強することになるだろう。

3小節による構造、あるいはより一般的に3つの拍節単位からなる構造は、その内部構造が(2+1)なのか、(1+2)なのか、あるいは区分が曖昧で1つのまとまりとして理解すべきなのか、しばしば決定が難しくなる。(2+1)構成の例として挙げたものも、(1+2)構成として解釈される可能性が十分にある。本研究では、そうした曖昧な対象の解釈を1つに決めることが理論の目標であるとは考えていない。曖昧なものは事実曖昧なのである。そのような場合には、可能な解釈を幾つか挙げ、その構造を説明することができればそれで十分であろう。そのような曖昧な形において、唯一の妥当な解釈を選ぶためにする議論は、より多くの観点が必要とされるものであって、この論文で扱う範囲を超えるものである。
3小節からなるフレーズは、さらに高次のアナクルーシスの可能性などを加味すると、上記の(2+1)と(1+2)の構成以外の場合がありうる。ありうる3小節構造のうち、3小節を区分せずまとまりとして処理する場合と、(2+1)の構成であると解釈する場合のみが、第4章の拍節構造の範囲内で理解可能な構成である。
第3節 リュシー標準形の装飾
フレーズの先頭の装飾:アナクルーシスとデキャピテ
もうすでにこれまでに挙げた譜例に出ているが、フレーズの先頭にはアナクルーシスを付加することができる。第5章ではこれをリュシーアーチへの一種の装飾として扱う。というのは、アナクルーシスの構造は第4章までで論じた拍節構造の範囲では説明できないからである。よって第5章ではアナクルーシスの付いたフレーズは、大雑把に強拍から始まるフレーズの少し装飾されたものとして理解される。アナクルーシスの構造を理解するための拍節構造の拡張は第6章で論じられる。

リュシーは、アーチの先頭付近の音のあり方を3つに分類している。アナクルーシスを持つ形とアナクルーシス持たず強拍から始まる形に加えて、強拍上に休符がある形をリュシーはデキャピテ(décapité「無頭の」)と呼んでいる。リュシーは、デキャピテの形では休符が本来その位置にあるべき音の代わりをしていると理解している。デキャピテに当たる構造は第6章の第2節『裏を取る形』以降でより詳細に論じる。ここでは、強拍の位置に休符が来ることがあるということだけ分かっていれば十分である。
注意しなくてはならないことは、アナクルーシスを持つフレーズと、デキャピテのフレーズは、しばしば外見が良く似てしまうということである。これを例を挙げて説明しよう。まず、譜例5-3.1はアナクルーシスを持つ形とみなして良いだろう。その場合、リュシーアーチを作る最初の強拍はアナクルーシスの後にある。

だが次の譜例5-3-2では、同じ形の上昇音形で始まるが、それより前に主要な強拍があると判断できるのでデキャピテとなる。このことは、メロディーの外観だけでは必ずしも判定が容易ではないことを意味している。

フレーズの終わりの修飾:アンジャンブマンとハイパーカタレクシス
リュシー標準形は、末尾にも装飾を付け加えることができる。ここでは、リュシー標準形の2つの拍節単位の後ろに音がはみ出した形を考える。

このようなはみ出しの処理として2つのパターンが考えられる。1つは、次のフレーズの先頭に重なるパターンである。このような形は、詩のアンジャンブマン (enjambement「句跨がり、行またぎ」)に喩えることができるだろう。アンジャンブマンでは、拍節の規則性を維持することができる。譜例5-3.2のようなデキャピテのフレーズの場合、このようなはみ出しが、丁度デキャピテの先頭の休符の位置に収まることになる。
もう1つのパターンは、はみ出した部分のために、余分な小節を与えるものである。この場合、結果としてリュシー標準形は拡大されて3小節フレーズに変わる。このような形を、詩の用語を借用してハイパーカタレクシスと呼ぶことにする。ハイパーカタレクシス(hypercatalexis)とは、詩行の終わりに余剰の音節を付け加えることであるが、ここではそれに伴って小節も増えるものとする。ハイパーカタレクシスは小節を増やしているので、規則性は破られているが、それ自体としてはもはや拍節構造からメロディーがはみ出しているとは言えないので、本来はこの節の「リュシー標準形の装飾」というカテゴリーには含まれない。ハイパーカタレクシスは、2小節フレーズの連続の中に3小節フレーズを出したり、あるいは4小節フレーズの連続の中で5小節フレーズを出す場合などで用いられる。不規則な構造については、第5章の第4節と第5節でより詳しく扱う。
こうして作られた3小節フレーズは、やはり(2+1)の解釈も、(1+2)の解釈も可能であるのだが、その部分がメロディーのはみ出しに1小節与えることによって作られたという解釈は(2+1)のグループ分けを促すだろう。何度も述べているように、本論文では、ある構造として解釈されやすいのかどうかをルール化したり、条件を決めたりすることを目標としていない。
メロディーの末尾からのはみ出しを、アンジャンブマンにして拍節的な規則性を維持するのか、ハイパーカタレクシスにして拍節的な例外を持ち込むのかは、作曲家の好みの問題である。例えばシューベルトはハイパーカタレクシスを選択する場合が多い作曲家である。

譜例5-3.3の『からす』の序奏は5小節である。最初の2小節は明らかに典型的なリュシー標準形によるフレーズである。その後、もう1度リュシー標準形が現れるように進行するが、第4小節のメロディーが止まらずに第5小節まで進んでトニックで終わっている。歌はその次の第6小節から始まるので、第5小節はハイパーカタレクシスによる延長であり、序奏は(2+3)のフレーズ構成となる。シューベルトはこのようにして5つ目の小節を序奏の延長に用いることを選択したが、この5番目の小節は作曲家の好み次第では取り去ることが可能である。次の譜例5-3.4の『道しるべ』も同様なことが言える。

フレーズの装飾とフレーズの区分
フレーズの前後に、リュシーアーチからはみ出したり凹んだりした部分を持つ事ができるのは、通常はフレーズのレベルやそれより上のレベルである。なぜならば、このような凹凸はフレーズの区切りとして感じられやすいからである。そのため、1つフレーズの内部構造に独自のアナクルーシスを付けると、フレーズはそのアナクルーシスによって分離しやすくなる。逆に、アナクルーシスを消し去ったり、アナクルーシスではないという解釈にすることによって、2つのフレーズが1つのフレーズに融合するということも生じうる。これは、装飾を持たないフレーズは拍節単位と同じ形になるので、高次の拍節構造の一部をなすものとして理解され易くなるためである。
第4節 フレーズと拍節の階層性
ウメコミ
本章の第1節において、リュシーアーチを拍節単位の分割のスキーマから得ているのだから、リュシーアーチを構成する拍節単位をさらに分割すれば、そこに入れ子状になった小さいレベルのリュシーアーチができるのは必然である。この時、図5-4.1のように、小さなリュシーアーチが、上のレベルのリュシーアーチの始まりや終わりに埋め込まれているように見えるだろう。このようにして、リュシーアーチの中にリュシーアーチを埋め込むことによってフレーズを細分化していくことができる。本論文では、このような操作やその結果生じる形をウメコミ(embedding)と呼ぶことにする。

ウメコミを繰り返すことによって区分は細かくなっていく。次の図5-4.2はスキーマを細分化していく過程の1つの例を示している。まず全音符は1:1で等分割されている。その結果生じる1つ目の2分音符は3:1の分割が適用され、さらにそこで生じた8分音符が3等分されている。2つ目の2分音符は1:1の分割が適用され、その結果生じる4分音符の2つ目には特別なイベントである休止がアサインされている。

このような細分化を、第4章で、書き換え規則の形で述べた。つまり、書き換え規則の1つの適用とこうした細分化の1つの操作は同等である。よって、このようにスキーマに修飾を加えて細分化して行っても、拍節的な書き換え規則の範囲内であれば、上位の分割の性質を維持したまま細分化されていくことになる。図5-4.2の分割は、最初に2/2拍子の分割が行われたので、その後にさらに細分化されても、2/2拍子の細分化としての性質を継承する。
リュシーアーチの終わりの拍節単位にこのような小さなリュシーアーチが埋め込まれる時「女性終止」と呼ばれる構造が生じる。このとき、フレーズの音の連なりの範囲の終わりの位置が後ろの弱拍側に延期されることになる。下の図5-4.3は、ベートーヴェンのピアノソナタ第1番Op.2-1の、第1楽章の最初の主題(譜例5-4.1)の時間区分を、ウメコミによって1つのリュシーアーチから構成したものである。リュシーアーチを作る2つの全音符のそれぞれに、このようなウメコミを施している。その際に、リュシーアーチの終わりに埋め込まれるのは先に示した図5-4.2の形全体であり、これは女性終止を作っている。一方、リュシーアーチの始まりへのウメコミはリュシーアーチの間を繋ぐような形になるので特別の名称は与えられていない。


高次のグループ
ある単位が複数集まって、あたかもそれが分割によって得られたもののように理解されると、高次のグループになる。つまり、実際に分割によって得られたかどうかには関わりなく、分割のスキーマによってそれらを理解した時、それらは高次グループとして感じられる。これはある複数の音を1つの小節の構成音として理解するような場合と全く同じである。分割のスキーマを適用できる限界についてはここで厳密に論じることはできないが、その限界は聴き手が拍節やフレーズの構造を感じることのできる限界と連動しているだろう。
人間が、把握しやすいものから先に把握すると仮定するならば、フレーズを作るレベル付近の、拍や小節のような構造を先に把握することになるので、それより大きなレベルは、拍や小節の組み合わせとして理解される。だから、高次グループとか高次拍節と言っても、そうした構造を出発点として理解することはできない。
フレーズがこのように集まると、より大きなレベルのリュシーアーチにフレーズを埋め込んだのと同じ構造になる。次の譜例5-4.2では1つ目の小節の先頭から、3つ目の小節の先頭への大きなリュシーアーチが見られ、その初めと終わりにそれぞれ図5-4.3で構成した形を埋め込んだものとみなすことができる。もちろんこれは、譜例5-4.2の4小節全体が1つのフレーズになると主張しているわけではない。なお、大きなリュシーアーチが、2つ目と4つ目の小節の間に生じているという解釈も絶対に不可能というわけではない。このような解釈を選ぶ場合については、第6章第1節で論じる斜拍子を参照していただきたい。

本論ではグループの生じる原因として拍節スキーマしか導入していない。よってここでの意味での高次グループの存在する限界は、拍節スキーマを当てはめられる限界と同じであり、拍節構造よりも高次のグループについてはここでは議論の対象としない。
「重なり」(オーバーラップ)について
フレーズにウメコミを行うと、一種の「重なり」(オーバーラップ overlap)が生じる。すなわち、埋め込まれるものの先頭は小さなリュシーアーチの先頭であると同時に、フレーズの骨格をなすリュシーアーチの始まりか終わりに一致するからである。例えば、譜例5-4.3では、2つ目の小節の先頭のラ♭はこの小節に埋め込まれたアーチの先頭であり、同時に1つ目の小節の最初のファから、2つ目の小節の先頭のラ♭までの2小節分の大きなアーチの終わりでもある。この場合、これらの「重なり」は1つのフレーズの内部の構造として生じているので、演奏の際に、このラ♭の音を前後どちらかにのみ所属させるのではなく、レベルの異なる2つの構造の要素になっているものとして理解されていなければならない。フレーズの内部の「重なり」は、ウメコミの存在する分だけ生じる。この意味での「重なり」は極めてありふれた現象であり、またグループを境界を最初に決めることによって分けることができると考えたGTTM理論のアプローチが誤りであると本論が考える理由でもある。
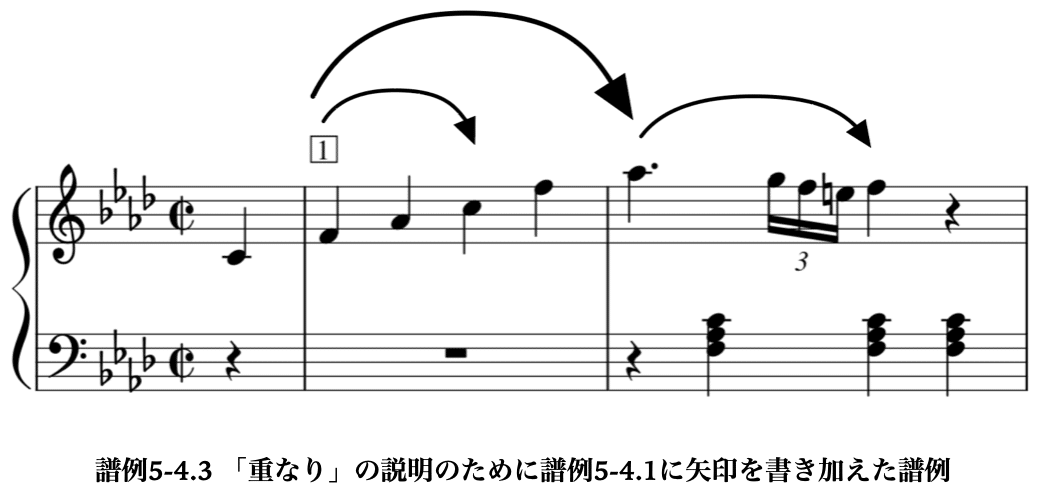
だが、フレーズより大きいレベルで見ると、この「重なり」はより抽象的なものになる。譜例5-4.2の3つ目の小節の先頭は、1つ目の小節の先頭からの大きなリュシーアーチの終わりであり、mm.3–4のフレーズは、これにウメコミを行ったのと同じ構造をしている。だが、この大きなリュシーアーチはフレーズの骨格ではないので、3つ目の小節の先頭は、ただリュシーアーチが重なっているだけで、フレーズとしては重なっていない。
以上の「重なり」は、規則的な拍節構造に基づくものである。より問題になるのは、フレーズやフレーズ同士の関係が不規則な拍節構造を伴う場合である。その時、不規則な拍節構造は、規則的な拍節構造を不規則的に連続させることによって生じ、その境界での「重なり」が、一般にオーバーラップとかエリプシスなどと呼ばれる構造に関係している。次の節では、このような不規則性について論じる。
第5節 規則的な拍節構造からの逸脱
歪んだリュシーアーチ
リュシーアーチは、拍節的な支配/従属の関係を表現している。それは常に、ある拍節単位内の強拍から弱拍へと形成され、その拍節単位の結合の骨格をなす。等時性スキーマに基づく基本的な場合では強拍と弱拍が2:2(=1:1)の関係をなすことになるが、第4章の不等分割においてすでに2:1の関係が等時性スキーマに則って構成される場合について論じている。ただしここでは2の連続が基準である場合を考えている。2:1は、2:2の構造の途中までが表面に現れた状態であり、そのために3拍子は(2+1)に分割され、それは4拍子を打ち切ったものとみなすことができたのであった。だから4小節構造の場合と全く同じように、3小節構造においても1つ目の小節の強拍と3つ目の小節の強拍の間にリュシーアーチを形成することができるのである。
これに対して2:3の関係は2:1と同じように理解することはできない。これは等時性スキーマにとって余剰の部分を含み、またその全体も5単位という単純ではないものになるからである。
しかし等時性スキーマとは、等時的ではないものを排除するためのものではない。例えば単純なビートでも、人間が演奏するならばタイミングに揺らぎが生じるであろう。そのようなものを大雑把に等時的なものとして理解するための構造が等時性スキーマなのである。というのも、長さがまちまちの音をそれぞれ正確に把握していたら人間の処理は追いつかないであろうからである。そして、タイミングの揺らぎは、スキーマの細かな修飾として処理されるだろう。その揺らぎに決まったパターンがあったり、単純な関係による場合などは、修飾のためのスキーマの存在が想定される。ビートを2分割や3分割するといったことも、このような修飾の一種である。
「歪み」とは、基準となるものがあるから「歪み」と言えるのである。だから歪んだ構造は、基準となる理解をもとにしてその修飾として理解される。2を基準とする際の、2:3の関係の間に形成されるリュシーアーチは、そのような等時性の「歪み」として、等時性スキーマとその一時的な修飾として理解されるであろう。
先行するものが従属する関係は拍節構造では理解ができないこと
ここまでは、リュシーアーチが維持される場合について述べてきた。だが、状況によってはもはやリュシーアーチが維持できない、あるいはその間にリュシーアーチが形成されない、といった形を考える必要が生じてくる。リュシーアーチは先頭側の強拍が支配的で、後続する側の強拍が従属する関係にあるが、フレーズでは場合によっては後続する側が支配するようになる場合が生じる。だが、そのような従属-支配のグループは、通常の拍節構造では表現できない。拍節構造では常に支配する側が先行するからである。このような後続する側が支配する関係の代表的なものはアナクルーシスである。だからアナクルーシスにおいては、通常の拍節構造における支配/従属関係を超えた新たな支配/従属関係を形成する構造が必要となる。第6章で、この役割を担う構造がシンコペーションであるとみなして拍節スキーマの拡張を試みる。
ワリコミについて
支配/従属関係にないというのは、同一のグループに属していないということである。ただし、漠然とした弱い支配/従属関係まで含めて考えれば、1つの楽曲全体や、複数の楽曲の集合全体も1つのグループということになってしまうであろうから、ここでは拍節構造に関わりがある程度のレベルに焦点を当てて考えることにしよう。規則的な拍節構造がはっきりしているならば、その範囲は大きく1つのグループとみなせるであろう。特に拍節構造がはっきりと感じられる数小節程度の規模の範囲であればそれが明確である。
しかし、規則的な拍節構造が終わり、異なる規則に従った別の拍節構造が新たに始まる時、そこにはグループの境界ができることになるだろう。それぞれが別々の支配/従属関係に属することになるからである。
この時、先行するグループが終了する前に、あたかも割り込んでくるかのごとく、次のグループの先頭が始まってしまうということがしばしばある。このような場合には、メロディーは連続しているが、グループの境界がその途中にはっきりと形成されるということになる。本論ではこのような、メロディーの接合を伴いながら支配的な拍節構造が変化するような場合を「ワリコミ(cut-in)」と呼称することにする。ただし第6章第2節で「弱いワリコミ」を定義するので、ここで論じるものは「強いワリコミ」ということになる。「弱いワリコミ」は、支配的な拍節構造を維持したまま、支配的な拍節構造に従属するずれたグループを割り込ませることであるが、このようなタイプの支配/従属関係は第6章の主題である。これに対して「強いワリコミ」は、接合し合う2つの構造が支配/従属関係を作らず、その接点を越える際に支配的な拍節パターンが変化する。これは、後から始まる部分によってパターンが書き換えられるように感じられるだろう。
ワリコミは、エリージョン(elision)とかエリプシス(ellipsis)などとも呼ばれるが、これは省略を意味している。だがここで論じるワリコミは、2つのグループの重なり合いのことであるから、「省略」ではこの意味を十分表現できないだろう。ワリコミは実践において、あとから始まる構造が、先行する構造を途中で打ち切るように接合することによって、まさに割り込むかのように用いられるものである。また、オーバーラップ(overlap)という用語も用いられるが、これはもっと曖昧である。本論ではすでに前節の第3項で、ウメコミの操作の結果として、拍節的な不規則性を伴わない場合にも「重なり」が生じることを見て来ている。
強いワリコミの例
ワリコミはリュシーアーチの終わりの位置に、新しいグループの最初の強拍を割り込ませることによって作ることができる。強いワリコミでは、この過程で支配的な拍節のパターンがずれることになる。つまりここで論じるワリコミは、境界の前後がそれぞれ独自の支配的な拍節構造を持っている。譜例5-5.1は1つの典型例であろう。まずm.44から、4小節+4小節の拍節的に安定したグループを出そうとする。譜例5-5.2は想定される安定的な8小節構造である。だが実際の音楽では、この最後の和音に当たる位置でワリコミを行い、そこから4小節構造を開始しようとする。その結果、先行する部分の拍節構造と、m.51からの拍節構造には、不整合が生じる。この実例ではさらに、m.51からの4小節構造の終わりにもワリコミが行われている。これが強いワリコミであると言うのは、m.51やm.54で、それまでの拍節パターンを上書きしているからである。ところが場合によっては、完全に書き換えがなされず、先行する部分の拍節構造を維持したまま新しい部分が割り込む場合がある。その場合、2つの部分は支配/従属関係に置かれることになり、強い結合が生じる。しかしここで挙げている例のような場合では、先行する部分の拍節構造がワリコミの後も維持されるということが難しいので弱いワリコミは成立しない。


次の譜例5-5.3は、(4+4+4)の12小節構造の最後にワリコミが出たものである。12小節のうち、後ろの2つの4小節構造(mm.5–11)が繰り返しなので、m.12でワリコミが起こっていることがよく分かる。m.12には、m.8と同じものが来るはずであったのだ。

以下、いくつか例を挙げておこう。ワリコミは一般的には、8つ目の要素が出るはずだった所や、4つ目の要素が出るはずだったところで行われることが多い。これは最後のリュシーアーチの終わりの位置であり、ワリコミの関係は、この割り込まれた最後のリュシーアーチの性質を継承している。よってワリコミは、ウメコミの際の埋め込まれるものが大き過ぎた場合と理解することもできる。通常のウメコミは、埋め込まれるものを完全に支配下に置くことになるわけだが、埋め込まれたものが大き過ぎるためにもはや支配が及ばなくなって、それぞれが独立した状態になったものが強いワリコミであると考えても同じことである。



なお、譜例5-5.1のm.51の右手の最初の和音は、本来の8小節目に出るはずだったものと解釈することが可能である。このような場合には、すでにこの章の第3節第2項で論じた「アンジャンブマン」と同様に扱われる。一方、譜例5-5.6のm.10のような旋律が完全に切れている場合は、ワリコミ以降の部分全体が、先行する部分の終わりの部分であるかのような印象を与えるだろう。
強いワリコミが用いられる典型的な場合として挙げられるのは、歌曲の間奏や終奏の始まりを歌の終わりの小節と同時にすることである。ワリコミは強拍から始まるのであるから、譜例5-5.7では元々序奏にあったアナクルーシスは消去されていると考えるべきである。譜例5-5.8は、伴奏の右手にもアンジャンブマンが生じている。なおこの2つの例はどちらも、(2+2+2)小節構造の6小節目にワリコミを持つ例である。

(動画の1:41からが譜例の箇所。動画の冒頭と比較してみてください。)

強いワリコミは拍節の規則性を乱すので、舞曲ではほとんど見られない。また、規則的な拍節構造を好むショパンのような作曲家では曲のジャンルを問わず強いワリコミはほとんど見られない。強いワリコミが頻繁に見られるのは、舞曲的な性格を持たないソナタ形式の第1楽章などである。
カテゴリー:音楽理論
