１６０年に及ぶ素数のナゾ、あと化学とかー続編３：数学の素数定理との見比べ
前回のNOTEでは、素数と高度な化学を融合させてみようという試みをしました。周期表の周期（２×ｎ×ｎ）の代わりに電子の魔法数を周期点として使って１万までの数字を分類したところ、Fig.4’ のオレンジ色のエリアで表したとおり、魔法数から等間隔に素数が２０個程存在するという不思議な規則性が見られました。
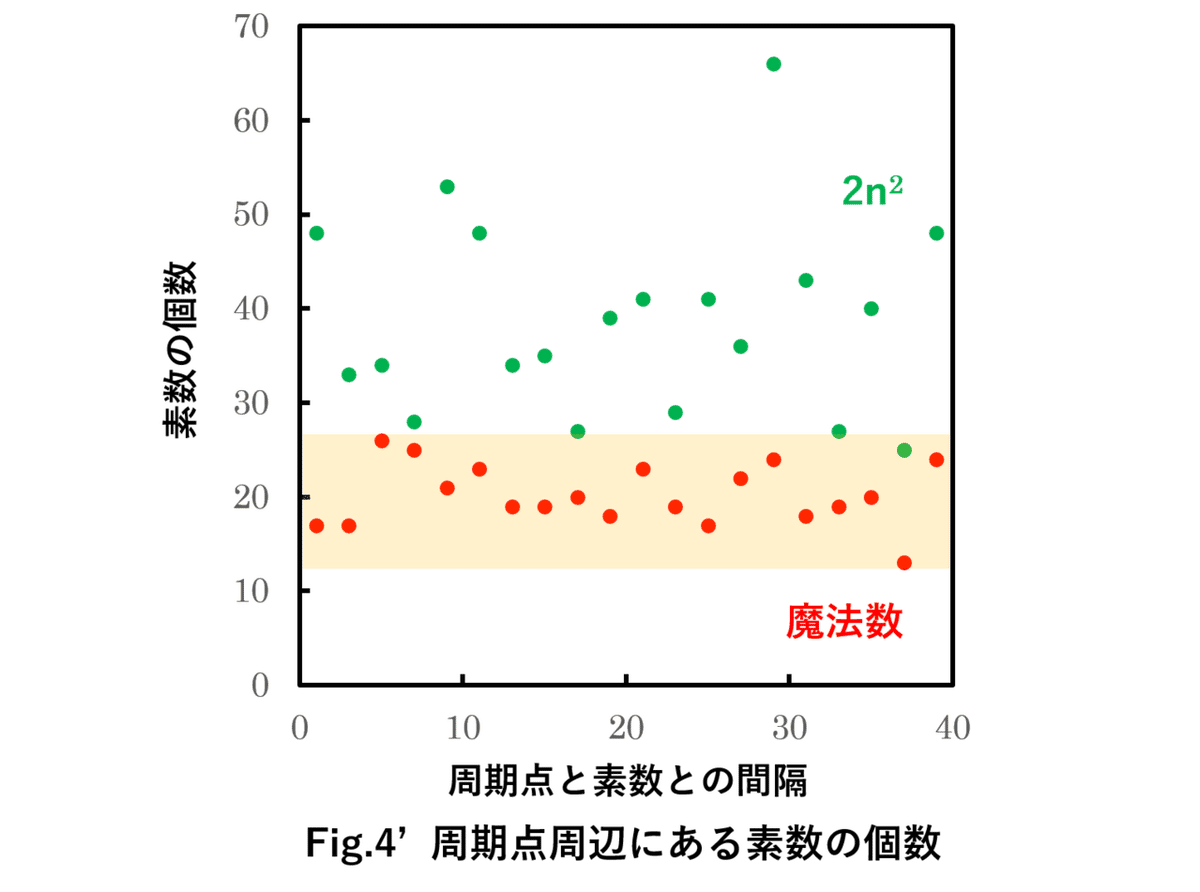
この現象に対して「具体的に、どんなイメージなら分かりやすいんかな？」と考えたとき、ふとしゃぼん玉の虹色模様が思い浮かびました。虹色模様には、赤や青といった様々な色のエリアがたくさんあります。その中でも特定の色（例えば、赤なら赤）がこの素数の個数２０を表していて、飛び飛びになっている同じ色のエリアが魔法数に対応しているようなものだろう、と空想していました。
それでは、前回からの続きに参りましょう。
①周期表の周期： ２、８、１８、３２、５０、７２、９８、１２８･･･
②電子の魔法数： ２、１０、１８、３６、５４、８６、１１８･･･
③１０の累乗 ：１０、１００、１０００、１００００、１０００００･･･
今回は、数学（素数定理）で行われている③１０の累乗（１０＾ｎ）ごとに分類したものと比較してみます。分類方法は下の通りです。
ｎ＝１（ １～ １０ ）のエリアに素数は ４個
ｎ＝２（ １１～ １００ ）のエリアに素数は ２１個
ｎ＝３（ １０１～１０００ ）のエリアに素数は １４３個
･･･ と言う風に数えていきます。
①～③の分類方法を使って、１００万（＝１０＾６）までの範囲で素数を数えた結果を下にまとめました。
大きなスケールに対応するために対数グラフを使ってみました。
見方としては、１目盛ごとに１０倍スケールになっていきます。灰色の補助線はそれぞれの桁の数１～９を表していて、グラフの左下隅から、
１，２，３，･･･７，８，９，１０，２０，３０，･･･７０，８０，９０，
１００，２００，３００，･･･７００，８００，９００，１０００，･･･
という感じになっています。
３つの分類方法のうち、青点で表した③１０の累乗ごとに分類する方法が一番グラフの上側にある理由は、周期別の幅が一番広くて（言い換えると、区分する点数が少ないため）その範囲内に出現する素数が多くなるためでしょう。
ちなみに、１００万までに区分した点の数は次の通りです。
①周期表の周期（２×ｎ×ｎ） ７０７点
②電子の魔法数 １７９点
③１０の累乗 ６点
それと、書き加えた３本のラインの傾きは違うものの、ライン付近には点がよく集まってきています。このことから、素数が出現する確率は多少のブレはあるものの、それぞれのラインの傾きに従った一定値に向かっていくことが分かります。
今回はここまでとして、冒頭で言っていた魔法数周りの素数２０個の不思議についての考察は、次回に持ち越します。面白い！と思っていただければ、サポートをよろしくお願いいたします ٩( 'ω' )و
この記事が参加している募集
「ためになるわ」と感じて頂ければサポートを頂ければ幸いです。よろしくお願いいたします。