【15ゲーム拡張パズル】63ゲーム20連タイムアタックしたら、頭が炸裂した
1.はじめに(目的)
本エッセイはナンバーパズルでプレーできる(大きさ4x4の)15ゲームの拡張版、(大きさ8x8の)63ゲームの平均タイムを測ってみようというNOTEです。今まではクリアタイム3分を切るためのNOTEを3つ書いてきましたが、1ゲーム勝負では初期配置運に因るところが大きいので、複数ゲームをこなしたデータから自分の平均的な実力を見極めます。体感平均値は2分50秒なのですが、そこからどれほどズレがあるかどうか実際にプレーして見ていこうと思います。
2.実験(プレーイング条件)
63ゲームは初期配置によってタイムが縮まったり伸びたりします。例えば、下図の通り1ゲーム目に左上隅にあった1が、2ゲーム目に右下隅に配置された場合、クリアタイムに大きな差が出ます。初期配置が完全ランダムに並んでいるという前提であれば、初期配置をえり好みしなければ信頼できる平均値を出すことができるはずです。そこで、初期配置を選ぶ権利を捨てて、1ゲーム目から20ゲーム目をクリアするまで20回連続のタイムアタックをしました。なお、各ゲーム間のインターバル(休憩時間)は全て10秒未満としました。

3.結果
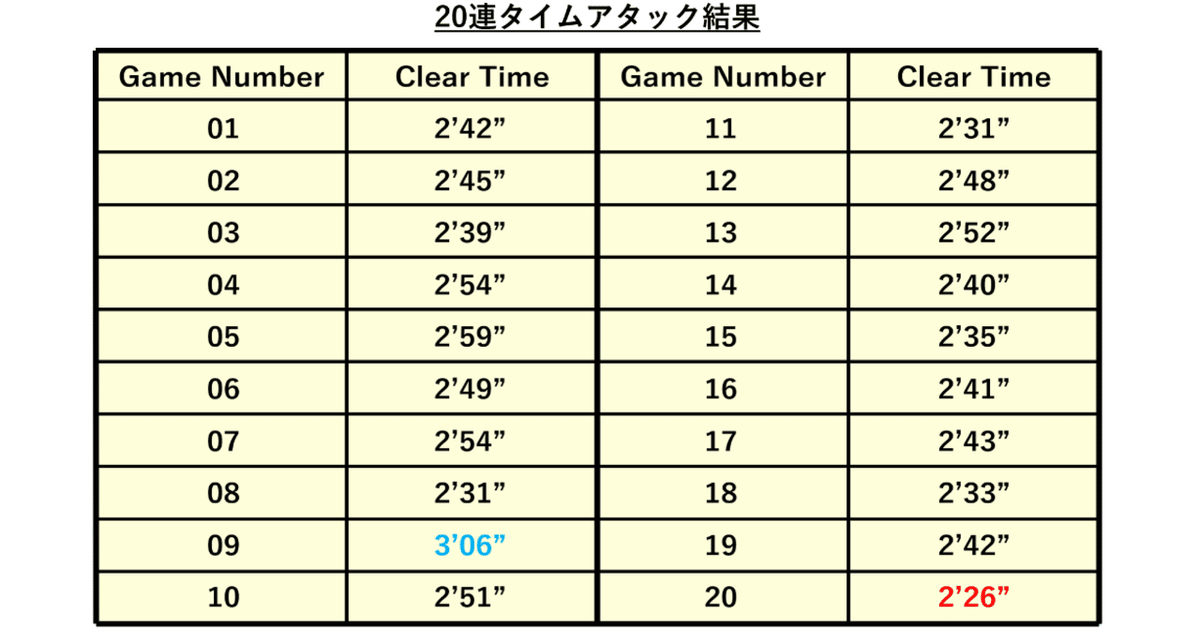
20連タイムアタックをした結果を下の表に示します。

最速は20ゲーム目の2分26秒、最遅は9ゲーム目の3分6秒、トータルプレー時間は54分41秒でした。ちなみに、ラスト20ゲーム目のプレー中は頭が炸裂するほどの疲労感に襲われていました。人間の集中力が持続する限界は30分程度なので、かなり無茶をしたと言えるでしょう。
4.考察
まずは平均タイムを計算します。20連タイムアタックにかかった時間(54分41秒)をトータルゲーム回数20で割ると平均2分44秒となり、体感平均値より少し短いタイムになりました。今度は、データが見やすいようにクリアタイムを10秒ごとに区切った棒グラフにプロットしてみます。

キレイな山の形(科学用語で正規分布)になりました。視覚的にも、平均値は2分40秒~2分49秒の間にあるだろうということが分かります。
余談として、自分のベストスコア2分14秒がどれくらいの確率で出るのか統計学を使って計算してみます。
確率はここの「信頼区間に対する信頼度の推移」表にある信頼区間と信頼度の対応を見れば分かります。必要なデータを下に書き出しました。
確率を求めたいデータ(d) = 2分14秒
平均値(μ) = 2分44秒
標準偏差(σ) ≒ 10秒
標準偏差(σ)は偏差値の計算に使われる数字で、偏差値は【50+10×(μーd)/σ】の数式で計算できます。
数字が大きい方が優れているテストの点数などの偏差値は
【50+10×(dーμ)/σ】の数式で計算します。
いま、1回プレーした時のタイムが2分44秒±10秒(=μ±1σ)の間に収まる確率を知りたい時、表の信頼区間「1σ」のところを見ます。すると、68.26・・・%と書かれているので、1回プレーすれば大体68.3%の確率で2分44秒±10秒のタイムが出ることが分かります。
それでは、2分14秒(=μー3σ)の場合はどうでしょうか?表の信頼区間「3σ」のところを見てみると99.73・・・%と書かれています。これは、1回プレーすれば大体99.7%の確率で2分44秒±30秒(=μ±3σ)のタイムが出ることを意味します。
言い換えれば、2分14秒以下のタイムと3分14秒以上のタイムが出る確率は0.3%(=100%-99.7%)であり、そのうち2分14秒以下のタイムが出る確率はその半分の0.15%ということなります。つまり、2分14秒は1000回プレーして2回出るかどうかという確率になるので、狙って出すのは不可能なレベルと言っても良いでしょう。ちなみに、タイム2分14秒の偏差値は80.1とめちゃくちゃ高いものでした。
5.まとめ
63ゲームにおける実力は体感平均値2分50秒を少し下回る2分44秒だということが分かりました。また、ベストスコア2分14秒は統計学的には1000回プレーして1~2回しか出せないほど低い確率であることが分かったので、記録更新はしばらくお預けとなりそうです。
6.今後の展望
20回というゲーム回数が少ないかもしれないので、20連タイムアタックを何度かプレーして、もう少しデータを増やすことで信憑性を上げたいと思います(やるとは言っていない)。
ここまで読んでいただきましてありがとうございました ٩( 'ω' )و
いいなと思ったら応援しよう!

