
WHAT IS TIME
はじめに
「長方形の面積を横×縦で計算したらバツにされた」
小学校の算数でこの問題が起きます。学校では縦×横で教えているので、その通りに記述しないと間違いになるのです。もう何十年も前から議論されているのに未だ決着がつきません。交換法則があるので横×縦でも間違いではないはずですが、教えた縦×横の形でないとバツにされるのです。
この議論の時にいつも気になるのが『子どもの声が聞こえない』ことです。数学の法則を知っている大人同士ばかりが議論していて、子どもがどう考えているのかが置いてきぼりになっているのですよ。
横×縦で解く場合はほとんどが、
「交換しても同じ答えになるから」
「そっちの方が計算しやすいから」
などの理由からでしょうし、それで正しいと思います。
しかし、それ”以外”の理由があるかもしれません。だから、大人から見てどうとかではなく子どもの話を聞かなくてはいけないのです。
そんなことを考えていたときに、自分はどうだったかな〜と記憶を辿ってみると「そういえばこんなことがあったな」と思い出したことがあります。こうすると縦と横が”入れ替わる”のです。
いろんなことで”入れ替わる”ことが起きているのに、気づいていないかもしれませんよ。
【時系列】
1. 時間の経過に従って定期的に観測して得た値を整理・配列した系列。
気象や経済事象などを数量的に分析して示す際に用いられる。時間数列。
2. 俗に、時間の経過の順に物事を配列すること。
Bob James - Westchester Lady
6歳の子供に説明できなければ、理解したとは言えない。
Interchange
縦×横 = 上下の横線×左右の縦線 = 横×縦
長方形の図と、その縦と横をそれぞれ別々に書いたものです。

①… 上下の横線
②… 左右の縦線
と、なっています。教えられた通りに縦×横で長方形の面積を求めるなら、
②×①
と表記すれば教えられた通りの順序になります。
が、ここでちょっと待ってください。
先ず①をよく見てみると横線が上下にありますよね。そして、その上下の”間”にあるものは『縦』なんですよ。縦の幅を上下の横線が表しているのです。
上下の横線 = 縦の幅
です。ということは、縦と横が”入れ替わり”ましたね。『=』とは等価交換ですので代入ができるはずです。縦と横を等価で 代入= 入れ替え できますね。それと同じように②を考えると、
左右の縦線 = 横の幅
となります。ここでも横と縦が”入れ替わって”います。まとめると、
①… 上下の横線 = 縦の幅
②… 左右の縦線 = 横の幅
こういう捉え方をした場合でも横×縦で表記してしまうのです。ほとんどは、
「交換しても同じ答えになるから」
「そっちの方が計算しやすいから」
との理由から横×縦をしているでしょう。ただ、縦と横を入れ替えて認識する場合があることを言いたいのですよ。だから大人同士で議論するだけではなく、子どもの話を聞かないといけないのです。
予想ですが、この認識の仕方は発達障害などにも関係してくるものかもしれません。
AとBを ⇒ AにBを ≠ AをBに
12 × 34 = 408
このかけ算の式を『筆算』でやるとちょっとおもしろいことになります。
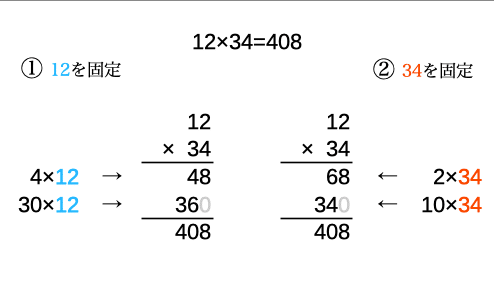
ほとんどの人が①をやると思います。『12 に 34 を かける』形ですね。ところが②をやってしまう人もいて、こちらは『12 を 34 に かける』形です。
①... 12 に 34 を かける
②… 12 を 34 に かける
2つを見比べてみると”に”と”を”の位置が入れ替わっていますね。本来、12×34の式の意味は『12 と 34 を かける』なのですが、筆算ではどちらかを”固定”するので”と”ではなく、”に”と”を”のように認識してしまうことがあるのです。
②を①の形に揃えるなら、
34 × 12(= 34 に 12 を かける)
としなければなりません。まさに交換法則ですね。これだと筆算でも、12が上の段で34が下の段にするのではなく、34が上の段で12が下の段になります。実は②は、34が上の段で12が下の段のやり方なのです。それを①の形のままでやってしまったのです。
交換法則は前後を入れ替えても答えが同じだからできるのでした。が、確かに答えは同じなのですが、途中が違っているのです。数学の問題では『答えが合っていても途中の式が違っていればバツになる』ことがありますが、それに倣うのであれば、①の前後を交換して②の状態で解くとバツにしなければなりません。交換して解くとバツにしなければならないのです。途中の式が違うのですから。
そういえば小学校の頃に答えが合うまで5・6回かかった筆算の問題がありました。答えを出して先生のところに持っていくのですが、なかなかマルがもらえませんでした。1回目や2回目は計算ミスで”答えが間違っている”ことも考えられたのですが、3回目4回目は何回計算しても同じ答えが出てくるのです。消しゴムで消しても”筆跡”は残りますから、前の答えと同じはずなのです。それなのにマルはもらえない。
もしかしたらそれは途中の式が間違っていたからかもしれません。①の形で筆算をするときに②の形で出てくる途中の式を書いていたのかも… まぁ今となっては確かめようもありませんが。
だから子どもの声を聞くべきなのです。
筆算では基本的に”上の段”の数字を固定するのですが、交換法則のことを考えると”下の段”の固定も認められます。
a. 答えは同じ… (結果は同じ)
α. 途中は違う… (経過は違う)
自分がした ≠ 相手がした
これは聞いた話なのですが、転職において会社側がスカウトを出すことがありますよね。このときもA社がKさんにスカウトを出して面談になりました。その面談のときにA社がKさんに、
「なぜ、我が社を選んだんですか?」
という質問をしたそうです。Kさんはそれに対しものすごい”違和感”を感じました。というのも、スカウトを出したのはA社であり、Kさんはスカウトがきたから面談に応じたからです。だからこの場合はKさんがA社に対し、
「なぜ、私をスカウトしたのですか?」
と質問するべきだ。ということです。
この話もまさに”入れ替わって”いるんですよ。
p. A社が、Kさんを選んだ
q. Kさんが、A社を選んだ
A社の質問からして、A社は q だと認識しているんですね。ということは、
自分がスカウトをして面談している のではなく、
相手が望んだから面談をしている と”入れ替え”ているのです。
スカウトは検索に引っかかった人全員に自動で送っているとか、そういう話じゃないんです。どんな検索にせよ”入れ替え”ていることが問題だと言いたいのですよ。なぜなら、ここで入れ替えているなら他のことでも入れ替えが起こっている可能性があるからです。
自分がした ことなのに、
相手がした ことになる。
その会社の上空ではカラスが鳴いているかもしれません。
TIME ∞ EMIT
『横書き』の文章を読むときは”左から右”に向かって読みます。今読んでいるこの文章もそうなっていますね。右から左なんてことはありません。必ず”左から右”に向かって読みます。
ということは『時間』は”左から右”に向かって流れているということです。右から左ではなく、左から右に向かって時間は流れていると無意識に刷り込まれているのです。時間は左から右。これを覚えておいてください。
数式は時系列を記述しない
カレーは、じゃがいも・にんじん・玉ねぎでできています。水とかルーは省きますね。これを式にすると、
p. じゃがいも+にんじん+玉ねぎ = カレー
となります。しかし、もう1つ表し方があって、
q. カレー = じゃがいも+にんじん+玉ねぎ
です。こっちは欧米の表し方ですかね。日本のと比べて左辺と右辺が入れ替わっています。これがちょっと問題で、横書きの文章を読むと時間が”左から右”に流れますから q の形だとまるでカレーから食材に戻せるかのような錯覚を生んでしまうのです。現実には時間は逆行しないのに、数式にした途端、まるで逆行できるかのように捉えることができるのです。
なぜ、こうなるのかというと、数式は時系列を記述しないからなんですね。単純な数字の計算でも、
p. 1 + 1 = 2
q. 2 = 1 + 1
この2つはどちらの表記でも正解です。しかし、モノやコトを数式で表すと p は成り立つけど q は成り立たないことがあります。横書きの左から右に時間が流れていくことを考えると q は時間の逆行になっているからです。
『=』 ⇒ 『≤』
① E = mc^2 … アルベルト・アインシュタイン
② F = ma … アイザック・ニュートン
③ 0 ≤ dS … ルドルフ・クラウジウス
有名な物理の数式です。『=』には時間の流れが含まれないことはカレーの式からも判りました。では、どうやったら時間の流れを表せるのかを考えて思いついたのが③の『≤』です。③は”エントロピー増大の法則”というものです。この記号により時間の流れる方向が決まるのです。左辺から右辺はあり得るのですが、右辺から左辺はあり得ません。カレーの式をそれに倣って書き換えると、
食材 ≤ カレー
(0 ≤ dS)
となります。
『時間の流れる方向』が決まりましたね。
現実の世界で起こっているモノやコトを数式で表すことは、その方が判りやすくなるからだと思いますが、『=』だと時間の流れを含まないことを忘れてしまうことがあるかもしれません。だから、最終的に出した答えを見ながら、
「時間の流れはどっちからどっちだ…?」
と考えてみて、流れがあることを記述したいなら『≤』に変えればいいのです。
不等号だと意味がおかしくなるなら『→』などでも構いませんよ。時間の流れる方向があり逆行しないことが伝わればいいのですから。時間の流れも含めて記述すると、
カレー ← 食材 ⭕️
カレー → 食材 ❌
食材 ≤ カレー ⭕️
などですね。
食材 = カレー ❓
『=』だと時間の流れが判りません。
数字 ≠ 現実 = 五感
「現実を見ろ」
仕事の結果を表す数字を見た上層の人が、思っていたような数字が出せていないことを指して、現場の人に向かってこう言うことがあります。これがすごく不思議なんですよね。というのも数字は数字であって現実ではないからです。
数字、文字、記号。
これらは頭の中のイメージを目に見える形にしただけのものであり、現実ではありません。現実とは五感を使って感じ取るものですが、数字や文字は視覚だけしか使っていないのです。そんなものが現実なわけないでしょう。漫画を読んで現実だとは思いませんよね。漫画/絵も視覚だけしか使いませんからね。
現実とは五感を使い、
言葉を話す
耳で音や声を聞く
目で見る
身体を動かし筋肉を使う
周りの匂いを嗅ぐ
食べたり飲んだりする
触れて温度や質感を感じる
こういったことの上に成り立つものが現実です。数字や文字、漫画が現実なわけないのです。この認識のズレが上層と現場の意思疎通を困難にしているのです。
上層にとっての現実… 数字
現場にとっての現実… 五感全てを使ったもの
ってことです。まったく認識しているものが違いますね。加えて、数字は結果ですから『止まった時間』ですが、五感を使うときは常に『流れる時間』の中にいます。もしかしたら、止まった時間ばかり見ている上層は脳の中の時間が止まってしまうことがあるのかもしれません。五感を使わないことにより、時間の流れを感知する脳の器官が刺激されないので衰えていくのですよ。
じゃあ、それを解決するにはどうすればいいか考えてみたのですが、
・音楽を聴きながら仕事をする
・机の周りをウロウロする
この2つです。音楽は流れる時間の中でしか成立しない芸術ですので、聴きながら仕事をすることで無意識に時間の流れを感知することになります。その人が好きな音楽が良いでしょうね。興味のない音楽だと脳が情報を”遮断”することがあるので意味がなくなってしまうからです。好きな音楽を聴きましょう。
書類の確認や考え事をするときは机の周りをウロウロして足を動かすのです。足が動いて身体の位置が変わることは、流れる時間の中にいることと同義ですので、脳が流れる時間を感知している状態になります。
数字しか見ないことは漫画しか見ないことと同義です。だから『メタバース』に行こうとしているのかもしれません。海外のとある機関が調べたところによると、日本のメタバースは現実の世界とは遮断された『別の世界』を作ろうとしているようですから。
海外… 仕事場の延長としてのメタバース
日本… 別の世界としてのメタバース
『妄想の世界』でも作ろうとしているのでしょうかね。漫画やアニメなどのファンタジーの世界を作り、そこに住む。その妄想の世界を維持するために、現実の世界では人間が死ぬまで働く… とかですか?
会社の上層と現場の意思疎通が困難な原因の1つに『中層が多すぎる』というものが考えられます。だるま落としみたいな感じで、スコーン!と中層を吹っ飛ばせれば良いんですけどね。今の中層は”邪魔”にしかなっていないのですよ。
【因果関係】
2つの出来事が原因と結果という関係で結びついていること。あるいは結びついているかどうかを問題にした概念。
Acoustic Alchemy - Tete A Tete
このたびは 幣も取りあへず 手向山 紅葉の錦 神のまにまに
98%
「速くしろ!」
時間のない現代人はいつも急いでいます。昼飯もできるだけ早く食べたいから、店の人を急かすこともあるかもしれませんが、いつも思うのは、
「なんで自分で弁当を作らないのか?」
ってことです。
すぐに昼飯が食べたいなら最速の方法は、自分で弁当を作って持ってくることです。どんなに急いでも店に行って注文して料理が出てくるまでに10分くらいはかかるでしょう。でも、自分で弁当を作ればカバンから出すだけなので3秒くらいですね。
「速くしろ!」
と言っているのは『速くして欲しいから』ですよね。速さを求めている… それならやっぱり自分で作れば良いだけじゃないですかね? 自分で弁当を作って持ってくれば3秒で食べられるのに、わざわざ店に行って200倍もの時間をかけているんですよ。
ヒトとチンパンジーのDNAは98%同じです。
社内の作業にしても、たとえば”コピー”を他人に頼むと部数などを伝えなければならないので、5秒くらいはかかりますが、自分でやれば他人に伝える動作が省けるので1秒もかかりません。ここでもわざわざ5倍の時間をかけているのです。
・自分で弁当を作ることをやらず、店にいくことで200倍の時間をかける
・自分でコピーせず、他人に頼むことで5倍の時間をかける
ヒトとチンパンジーのDNAは98%同じです。
人は『習慣の生き物』ですので、200倍や5倍の時間をかけることをやっていると、他のあらゆる仕事を200倍や5倍の時間をかけてやるようになります。これが”残業だらけ”の原因なのです。それだけ無駄に時間をかけていたら、そりゃ残業だらけになるのは自明でしょう。
ん? 店の売上が心配? あ〜それは気にしなくても大丈夫です。というのも、『正規分布』を元にするなら速さを求める人は2.5%しかいないんですよ。その速さを求める2.5%の人が来なくなったら、代わりに真ん中の95%の人たちをガッポリ獲れば良いだけなので。
これっていわゆる『win-winの関係』ってやつですよね。速さを求める2.5%の人たちは自分で弁当を作って最速で昼飯が食べれるし、店も95%の人たちが獲れれば売上は上がりますからね。まさに『win-winの関係』なんですよ。
自分がやればいいことをわざわざ何倍もの時間をかけてまで、他人に頼む必要はないってことです。
ヒトとチンパンジーのDNAは98%同じです。
関わらない方が良い関係 ってのもありますからね。
時間は存在しない
物理学者のカルロ・ロヴェッリが『時間は存在しない』という本を書きました。物理の式を解いていくと t (時間)が消えるのです。これを聞いたときに、
「それと同じことがもっと簡単にできないかな」
と思いました。物理の式を考察することは難しすぎて手が出ないので、もっと簡単で身近なものを使って時間が消せないか考えてみたところ、小学校で習う式でも時間が消せることに気づいたのです。
① 速度 × 時間 = 距離
では、この式から『時間』を消してみましょう。
距離とはある地点からある地点までの長さのこと、つまり空間ですよね。なら、
距離 = 空間
です。さらに、速度とは距離を時間で割ったものですから、
速度 = 距離 ÷ 時間 = 空間 ÷ 時間
になります。これらを①に代入すると、
① 速度 × 時間 = 距離
空間 ÷ 時間 × 時間 = 空間
空間 = 空間
空間だけが残り時間が消えましたね。このことから、
時間とは、空間と物質(波動)の”比率”のこと。空間と物質(波動)の間に生まれるものではないか。
と推察しました。まぁこれ以上の考察は無理ですが、なんとなくそう考えられたのです。でも、推察の真偽はともかく、ちゃんと時間は消えましたね。実は上記の方法だと時間を残して空間を消すこともできます。その辺は大目に見てください。ただ、そうなると”速度は存在しない”なんてことにもなるんですかね〜… わかりません。
世界最高峰の物理学者が「時間は存在しない」と言っていて、そのことが自分が習った式でも証明できると知った子どもたちは、物理学に興味を持つかもしれませんし、算数をもっと頑張るなんてこともあるかもしれません。
自分が知っていることでもできる。
これって結構大事なことだと思いますよ。教育において「いかに興味を引くか」が決め手になったりするからです。
よく、光の速度に近づけば時間が遅くなると聞きますが、だったら光の速度からどんどん遅れていくと時間は速くなるのかな? と、考えたりしますね。
おわりに
算数のかけ算の順序を考えるとき、主語がおかしいんですよ。
「大人が…」
「法則が…」
どこに”子ども”がいるんですか? 子どもの話なんだから当然、
「子どもが…」
と、主語は子どもになるべきなのに突然消えてしまう。まるで数式からt(時間)が消えてしまったかのようですね。大人や法則は後回しでいいのです。
算数の問題で、
【パンが3個入った袋が5つあります。パンは全部で何個ですか。】
この問題を”習った通り”に解くなら、
3 × 5 = 15
です。これを子どもによっては、
5 × 3 = 15
として解いてしまう。こうなってしまうのはなぜかを考えてみたんですが、
「もしかして、逆行して考えているのか…?」
と考えました。5 × 3 は時間を逆行して考えた場合なのですよ。時間を遡って考えていくなら、5 × 3 の表記をすることになります。問題文を読んだ子どもが、
『5つの袋があって、それぞれに3個ずつ入っているのか。それなら…』
と、捉えているのです。これはまさに時間を遡って考えている。時間の逆行、つまり、『逆算』とも見ることができます。算数では逆算も習いますが、それとはちょっと違いますよ。でも、”思考の流れ”は逆算と同じではないでしょうか。
それならやはりバツにするのはおかしいなと思いますね。逆行して考えたらバツになるなら、逆算はすべてバツにしなければなりませんし、逆算を教えてはいけないなんてことにもなるでしょう。
ただ、子どもには『違う解き方』をしていることは伝えたいのです。ここで重要なことは、
間違い ではなく、
違う だけ、
ということです。時間の順行と逆行の2つは、どちらが”間違い”とかではなく、2つは”違う”だけですからね。数式で確認すると、
3 × 5 = 15 ← 順行
5 × 3 = 15 ← 逆行
ってことです。
『時間』に関わることで、答えは合っているけど表記が違う。これに区別をつけるなら、
p. 順行で解いたものにはマル。太陽『⭕️』
q. 逆行で解いたものには三日月。月『🌙』
と、してみると答えは正解だけど、君が書いたやり方は順行ではなく逆行になっていますよ〜と、示すことになります。もちろん点数は同点です。太陽も月も時間に大きく関わるものですから。
『⭐️』でも良いかもですね。星の光は過去から届いていますので、過去を見ている = 時間を逆行している とするのです。
算数のかけ算では数字の前後を入れ替えても同じ答えですが、数学の行列では数字の前後を入れ替えると違う答えになります。
p. 算数のかけ算 → 数字の前後を入れ替える → 同じ答え
q. 数学の行列 → 数字の前後を入れ替える → 違う答え
会社の面接では、
p. A社が、Kさんを選んだ
q. Kさんが、A社を選んだ
この2つでは違う答えになります。
昼飯では、
p. 自分が弁当を作る… 3秒
q. 店が料理を作る… 10分
この2つでは違う答えになります。
現実の世界では『自分がしたか、他人がしたか』によって、違う答えが出ることはよくありますね。”因果関係”なんかも逆にしてはいけません。
p. 余計な時間を使ったから、残業がある
q. 残業があるから、余計な時間を使った
前者は理解できますが、後者は意味不明ですよ。
「だったらなんで余計な時間を使ったんですか?」
と聞きたくなります。ヒトとチンパンジーのDNAは98%同じです。
それではまた〜☀️⭐️🌙
この記事が気に入ったらサポートをしてみませんか?
