
ギリシャ数学を読むということ

0.序
古代ギリシャ人は,現代の私たちが「科学」と呼んでいるものを考えだしました.ここでは,数学にスポットを当て,二千年以上前の数学に対して,今さらどのようなことを研究しているのかということを紹介したいと思います.
数学と,それ以外の科学の大きな違いは,古代の数学においても真であるとされた命題は,基本的に現代でも真であるということです.具体的にいえば,紀元前300年頃に書かれたとされる(※年代には異説があります),エウクレイデス(ユークリッドは英語名)『原論』第Ⅰ巻に収められている「三平方の定理」の証明は,今日でも正しいのです.
一方で,アリストテレスによる動物についての研究には,現代の目から見れば,荒唐無稽な議論も見られます(※たとえば無生物から生物が発生すること等).そこで過去の科学を研究するには,議論の前提や当時の常識をきちんと踏まえた上で,古代人の議論を評価する必要があります.
しかし数学というのは,すでに述べたように,二千年以上前の議論であっても,その内容は現代においても正しく,ともすれば,古代数学は現代数学の「サブセット(機能制限版)」のように見えてしまうでしょう.いまさら研究することなど何もないと思われかねません.
そこで,古代ギリシャ数学のテクストを研究することで,どのような新しい発見があるのかということを紹介したいと思います.今回は,『原論』のテクストに残された「奇妙な特徴」を検討することで,古代ギリシャにおいてどの様な数学の授業が行われていたのか分かる,という研究を紹介したいと思います.
この原稿は, Ken Saito "Diagrams and traces of oral teaching in Euclid’s Elements: labels and references," ZDM Mathametics Education 50(2018), 921-936 をもとに , 広く一般の方に向けて,数学史研究への関心を喚起するために用意いたしました.
1.『原論』のテクストの4つの「奇妙な特徴」
ギリシャ数学のテクストには現代の私たちが当惑する4つの特徴があります.
①命題番号がないこと
②図にアルファベット順に記号が割り当てられていること
③直線ABを直線BAと言い換えること
④言明(プロタシス)が長く,時には理解できないことがあること
ギリシャ数学のテクストには,命題番号がありません.私たちが目にする数学文献に番号があるのは,後世の編纂者が書き加えたものです.例えば『原論』の冒頭にある有名な「定義」は次のように書かれています.
Σημεῖόν ἐστιν, οὗ μέρος οὐθέν. Γραμμὴ δὲ μῆκος ἀπλατές. Γραμμῆς δὲ πέρατα σημεῖα.
ちょっと何のことだか分かりませんね.これに番号が付され,次のように翻訳されます.
定義1.点とは部分のないものである.
定義2.また,線とは幅のないものである.
定義3.また,線の両端は点である.
(※本稿における『原論』の邦訳は全て,斎藤憲『エウクレイデス全集』第1巻,東京大学出版会,2008年からの引用です)
非常に分かりやすくなりました.聞いたことがあるという方もいるのではないでしょうか? この定理の証明には「命題10を用いる」とか,「定義5に基づく」というように言える便利な方法です.ちなみに現代の教科書には必ず定理や公式には番号がありますね.

この(1)です.教科書を用いて勉強するときには大変に便利な番号です.この番号付けが,古代の数学文献には無いのです(※ただし紀元後2世紀頃には番号付けが始まっていたと考えられています).
次に,②の「図にアルファベット順に記号が割り当てられていること」を見てみましょう.(※図はEUCLID’S ELEMENTS OF GEOMETRY
The Greek text of J.L. Heiberg [1883–1885]edited, and provided with a modern English translation, by Richard Fitzpatrickから一部変更して引用しました)

命題36と命題37は,円と接線についての命題です.命題36では,円の中心はE,命題37では円の中心はFになっています.私たちの教科書では,例えば円の中心をOとすれば,最後まで,ずっと中心はOのままです.これは一体どういうことでしょうか? 実際に命題36を見てみましょう.
というのは,円ABCの外部に何らかの点Dがとられたとし,Dから円ABCへと二直線DC,DBが落ちたとしよう.
次に命題37です.
というのは,円ABCの外部に何らかの点Cがとられ,Dから円ABCへ二直線DCA,DBが落ちるとし,まずDCAが円を切り、またDBが円へ落ちるとし,またAD,DGに囲まれる長方形がDB上の正方形に等しいとしよう.私は言う,DB上の正方形は円ABCに接する.というのは,円ABCの接線DEが引かれて,円ABCの中心がとられたとしよう.それをFとし…(※訳の一部を変更した)
お気づきでしょうか? 証明に出てくる記号は,ABCDEF…つまりアルファベット順になっています.古代人には円の中心の記号をEやOとして固定して議論するという習慣がなく,文章の順番通りに記号を割り当てていくのです.
次に③の「直線ABを直線BAと言い換えること」を見てみましょう.
再び第Ⅲ巻命題37を見てみましょう.
ゆえに角FEDは直角である.…(中略)ゆえに角DEFは角DBFに等しい.
Eにおける角FEDが,同じ命題の中で角DEFとして反復されます.
これは現代の教科書では,まず見られない表現で,私たちを当惑させます.
「三角形ABCの面積は四角形Sの半分である.そこで三角形ACBの面積を求めよ.」と言われると困ってしまいます.
続いて④の「言明(プロタシス)が長く,時には理解できないことがあること」を見てみるのですが,その前に「言明」とは何か?ということについて説明する必要があります(※少しずつ難しくなります,頑張ってください).
『原論』に代表されるギリシャ数学の証明は以下の6つのステップによって書かれていることが多いのです(※この形式を指摘したのは紀元後5世紀のプロクロスです).
言明→提示→特定→設定(作図)→証明→結論
それでは『原論』第Ⅰ巻命題18を例に具体的に見てみましょう。
1. 言明:あらゆる三角形の,大きい辺は大きい角に向かい合う.
2. 提示:というのは,三角形をABCとし,辺ACがABより大きいとしよう.
3. 特定:私は言う,角ABCが〔角〕BCAより大きい.
4. 設定:というのは,ACはABより大きいから,ABに等しいADが置かれ,BDが結ばれたとしよう.
5. 証明:すると,角ADBは三角形BCDの外角であるから,内対角DCBより大きい,また角ADBは角ABDに等しい――なぜならば辺もABがADに等しいから(※――以降はエウクレイデスより後の編纂者による加筆と考えられています).ゆえに,角ABDも角ACBより大きい,ゆえに,角ABCは角ACBよりさおさら大きい.
6. 結論:ゆえに,あらゆる三角形の,大きい辺は大きい角に向かい合う.これが証明されるべきことであった.
これがギリシャ数学の形式です.この命題18の言明は単純で分かりやすいのですが,次の命題の言明はどうでしょうか?どうか我慢して,ゆっくり読んでください.
第Ⅲ巻命題37
もし円の内部に何らかの点がとられ,またその点から円へと2つの直線が落ち,まずそれらの一方が円を切り,また他方が〔円へと〕落ち、また〔円を〕切る直線の全体と,〔最初にとられた〕点と凸な円周との間に切り取られた直線に囲まれる長方形が,〔円に〕落ちる直線の上の正方形に等しいならば,〔円に〕落ちる直線は円に接することになる.
何を言っているのか分かる人はいるでしょうか? この言明だけで命題の意味を把握するのは困難です.続く「提示」を見てみましょう.
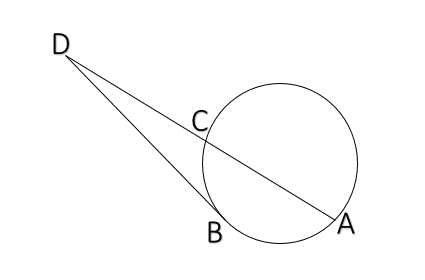
というのは,円ABCの外部に何らかの点Dがとられ,Dから円ABCへと2直線DCA,DBが落ちるとし,まずDCAが円を切り,またDBが円へと落ちるとし,またAD,DCに囲まれる長方形がDB上の正方形に等しいとしよう.私は言う,DBは円ABCに接する.
このように言われると,数学の得意な人は「ははーん,方冪の定理のことだな」とお気づきになるかもしれません(↓).
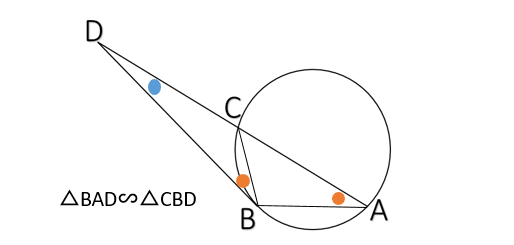
少なくともこの「提示」によって,これから何を証明しようとするのかが,読み手にとって明確になります.それでは何故,このような長くてわかりにくい言明が『原論』のテクストに保存されたのでしょうか?
2.書かれた数学と語られた数学
『原論』に代表される古代ギリシャ数学には,定理を番号で呼ぶ習慣がなく,辺ABと言ったと思えば,辺BAとも言い,円の中心をAとした図の次の命題では,円の中心をBと呼ぶ.そして長くて理解しにくい(※読むだけでも一苦労)の「言明」があります.私たちが当惑する『原論』の4つの奇妙な特徴は,「対話」によって数学が教えられていたと想定すると,むしろ自然なことだと思えてくるというのです.つまり,数学の授業というものが,一人の教師が黒板と本(教科書)を用いて複数人の生徒を教えるという形式ではなく,蝋板(※イラスト参照)を用い,または砂を撒き,その上に図形を描いて少人数の「対話」によって教えていたのだという想定です.

当時は,「本」というものはまだなく,書物といえばパピルスで出来た巻物でした.

たとえば,巻物から命題37を探す作業を想像してみてください.頁をめくるようにはいかず,巻物をすべて広げなければならないでしょう.すると定理や命題へ番号を与えることは,ほとんど何の役にも立ちません.
次に,直線ABを直線BAと言い直すことも,教師と生徒が対話によって授業をしていると想定すれば自然なことです.

ここでもう一度,蝋板や砂場を想像してみてください.次の命題を説明する際に,前の命題は消さなくてはなりません.私たちが普段使っているノートや安価な紙はないのです.すると,前の命題では中心をAとしていたものが,次の命題では中心がBになるのも不自然なことではありません.思い出してみてください,『原論』の証明のテクストでは,A→B→C(※ギリシャ文字では,A→B→Γ),というようにアルファベット順に記号が出てきます.これも教師が,前の図を消して,新しく図を書き直し,それを生徒に語りかけて説明していたのだと想定すれば自然なことです.蝋板や砂場に描いた図形に,語りかける順にアルファベット(記号)を割り当てていったのでしょう.
3. 記憶装置としての「言明」
最後に4つめの「奇妙な特徴」が残されました.「長くて分かりづらい言明」は何のために残されたのでしょうか? エウクレイデス以前の時代に,数学がどのように教えられ,議論されていたかについての文献は,プラトンの『メノン』(82b9-85b7)の有名な一節が知られています.ソクラテスが幾何学の訓練を受けていない召使いの少年に,与えられた正方形の2倍の面積になる正方形を見つける方法を「想起」させるシーンです.このシーンは「想起」としての知識のプラトンの説の証明となっています.対話の年代は紀元前402年頃,執筆の年代はおそらく紀元前380年頃と考えられています.このプラトンの対話篇が,彼の時代の数学の授業を忠実に再現したものであると断定は出来ませんが,ソクラテスの対話の次のような特徴は,プラトンの時代の授業の様子を反映していると考えても良いでしょう.
ここで,プラトン『メノン』の一節を引用します.
ソクラテス 「では、君、ぼくに答えてくれたまえ、正方形とはこのようなものだということがわかるかね?」
召使 「はい、わかります。」
ソクラテス 「ところで、正方形がもっているこれらの線 ―四つあるね― は、全部等しいものだね?」
召使 「ええ、たしかに。」
ソクラテス 「こうやってまんなかを通る線をひくと、これらの線もや
はり等しいのではないかね?」
召使 「はい。」
ソクラテス 「このような図形には、大きいのも小さいのもあるだろうね?」
召使 「ええ、たしかに。」
ソクラテス 「では、この辺の長さが二プゥスで、この辺が二プゥスだとすれば、全体は幾〔平方〕プゥスあるだろうか。こういうふうに考えてごらん。― もしかりに、ここが二プゥスで、ここが一プゥスしかないとしたら、この図形は二プゥスの一倍の大きさだということになるのではないかね?」
召使 「はい。」
ソクラテス 「ところが実際には、ここも二プゥスなのだから、この図形の大きさは二の二倍になるのではないかね?」
召使 「そうなります。」
プラトン『メノン』藤沢令夫訳,岩波書店,1974年.(※訳者による補足を省略した.)
この文章をみて,何について,どのような図形について議論しているか分かるでしょうか? ソクラテス(著者プラトン)は図形に対して,ABのような記号を用いていません.図形は「これ」とか「この」と指示代名詞で呼ばれるだけです.ソクラテスと召使いの少年の二人にしか分からないようになっています.しかし,召使いの少年には十分に理解できるものでしょう.教師が目の前にいて,砂に描かれた図形の辺や角を「これ」と指し示されることは非常に分かりやすいものです.エウクレイデスより古い時代,数学の授業は記号を用いず行われていたのです.すでに,古い時代,命題には番号がなかったことを見ました.命題番号がなく,記号も用いられない.すると当時の人はどうやって数学の定理を覚えていたのでしょうか?
私たちは,子供のころ数学(算数)の公式をどうやって覚えたでしょう.三角形や円の面積の公式って何でしたっけ?
そうです,

ですよね.三角形の面積をだすには,高さに1/2をかけて,底辺をかけても同じ(数学的には真)なのですが,必ず「底辺×高さ÷2」の順番で行ったはずです.こういった「丸暗記」というのは複雑な命題を覚えるときにこそ有効です.それでは,言明の丸暗記というものが実際に行われていたと考えられる証拠を,シンプルな例として『原論』第Ⅰ巻命題4と5にみてみましょう.
もし2つの三角形で,2辺に2辺が各々等しく,さらに〔一方の三角形で〕等しい2直線〔2辺〕によって囲まれる角が〔他方の三角形の等しい2辺によって囲まれる〕角に等しいならば,底辺も底辺に等しく,さらに三角形は三角形に等しく,残りの角も残りの角に,等しい辺が向かい合う角が各々等しくなる.
この言明を分類します.
(1) もし2つの三角形で,2辺に2辺が各々等しく,
(2) さらに〔一方の三角形で〕等しい2直線〔2辺〕によって囲まれる角が〔他方の三角形の等しい2辺によって囲まれる〕角に等しいならば,
(3) 底辺も底辺に等しく,
(4) さらに三角形は三角形に等しく,
(5) 残りの角も残りの角に,等しい辺が向かい合う角が各々等しくなる.
これを丸暗記していたのだとすれば,この定理を用いる証明で,このままの手順で証明を行うはずです.命題5の中で命題4が用いられるのですが,どのように用いられているのか見てみます.

すると,まずAZはAHに等しく,またABはAGに等しいから,そこで2直線ZA,AGは2直線HA,ABに各々等しい.さらに〔これらの直線は〕共通な角ZAHを囲む.ゆえに底辺ZGは底辺HBに等しく,三角形AZGは三角形AHBに等しく,残りの角も残りの角に,等しい辺が向かい合う辺に各々等しくなる.
それでは分類してみましょう.
(0) すると,まずAZはAHに等しく,またABはAGに等しいから,
(1) そこで2直線ZA,AGは2直線HA,ABに各々等しい.
(2) さらに〔これらの直線は〕共通な角ZAHを囲む.
(3) ゆえに底辺ZGは底辺HBに等しく,
(4) 三角形AZGは三角形AHBに等しく,
(5) 残りの角も残りの角に,等しい辺が向かい合う辺に各々等しくなる.
どうでしょうか?命題4の言明が,そのまま命題5で繰り返されているでしょう.『原論』はこういった構造で書かれており,そこには,本や記号のなかった時代に行われていた,「対話と言明の丸暗記」による数学の授業の痕跡を見つけることができるのです.
4. まとめ
『原論』のテクストを読むことで,二千年以上前のギリシャ人の数学の授業を復元するという魅力的な試みをご紹介いたしました.論文の著者は,「話し言葉」によって行われていた数学というものを強調しています.他にも紹介したことはたくさんあるのですが,それは次の機会にして,本稿はここまでといたします.最後までお読みくださりましてありがとうございました.
参考文献
Ken Saito "Diagrams and traces of oral teaching in Euclid’s Elements: labels and references," ZDM Mathametics Education 50(2018), pp.921-936
斎藤憲『エウクレイデス全集』第1巻,東京大学出版会,2008年
斎藤憲『ユークリッド『原論』とは何か』 岩波科学ライブラリー,2008年
