Lagrangeの運動方程式

解析力学のはじめの一歩として、ラグランジュの運動方程式による解法の簡単な例を示す。
ラグランジュの運動方程式(Lagrange's eqation of motion)とは
　$${\dfrac{d}{dt}\Bigl(\dfrac{\partial\mathscr{L}}{\partial \dot{q_1}}\Bigl)-\dfrac{\partial\mathscr{L}}{\partial q_i}=0      　　 (i=1,2,‥ ,f)}$$
　　$${\mathscr{L}}$$：ラグランジアン（ラグランジュ関数）
　　$${q_i}$$：一般化座標　　　　$${t}$$：時刻
　　$${\mathscr{L}=T-U}$$（$${T}$$：運動エネルギー､$${U}$$：ポテンシャルエネルギー）
$${\mathscr{L}(=T-U)}$$を代入した式を$${\dot{q_i}}$$､$${q_i}$$で偏微分､微分するのが手順である。

０ 簡単な導出
　Newton's eq　$${\bm{F}=m\bm{\ddot{x}}=\dfrac{d}{dt}(m\bm{\dot{x}})}$$　　(1)
　また　保存力$${\bm{F}=-\bm{∇}U}$$　(2)
(1)(2)より
　$${\dfrac{d}{dt}(m\bm{\dot{x}})=-\bm{∇}U}$$、成分で表わすと$${\dfrac{d}{dt}{m\dot{q_i}}=-\dfrac{\partial }{\partial q_i}U}$$　(3)

　また$${T=\dfrac{1}{2}m\bm{\dot{x}}^2=\dfrac{1}{2}m\sum\dot{q_1}^2}$$、$${\dot{q_i}}$$で偏微分すると$${\dfrac{\partial T}{\partial \dot{q_i}}=m\dot{q_i}}$$　(4)
(3)(4)より
　$${\dfrac{d}{dt}\Big(\dfrac{\partial T}{\partial \dot{q_i}}\Big)+\dfrac{\partial U}{\partial q_i}=0}$$　　(5)
ここで$${\mathscr{L}=T-U}$$とすると
　$${\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}=\dfrac{\partial T}{\partial \dot{q_i}}-\dfrac{\partial U}{\partial \dot{q_i}}=\dfrac{\partial T}{\partial \dot{q_i}}}$$（$${U}$$は$${q_i}$$のみの関数）　　(6)

　$${\dfrac{\partial\mathscr{L}}{\partial{q_i}}=\dfrac{\partial T}{\partial {q_i}}-\dfrac{\partial U}{\partial{q_i}}=-\dfrac{\partial U}{\partial{q_i}}}$$（$${T}$$は$${\dot{q_i}}$$のみの関数）　　(7)
(5)(6)(7)より
　$${\dfrac{d}{dt}\Bigl(\dfrac{\partial\mathscr{L}}{\partial \dot{q_1}}\Bigl)-\dfrac{\partial\mathscr{L}}{\partial q_i}=0      　　 (i=1,2,‥ ,f)}$$

（いまのわたしには、何故わざわざ$${\mathscr{L}}$$を定義するのか、(5)に直接$${T}$$と$${U}$$を入れて処理してはだめなのか。この疑問に答えることは出来ない。これからの課題である）
追記　(7)は$${\dot{q_i}}$$のみの関数ではない。極座標では$${q_i}$$も入る。（例えば 5 惑星の運動）上のような説明はネット上でも散見するが、直交座標の時の説明である。一般化座標系での説明を後述する。

１ 自由落下　　$${f=1 （  x  ）}$$

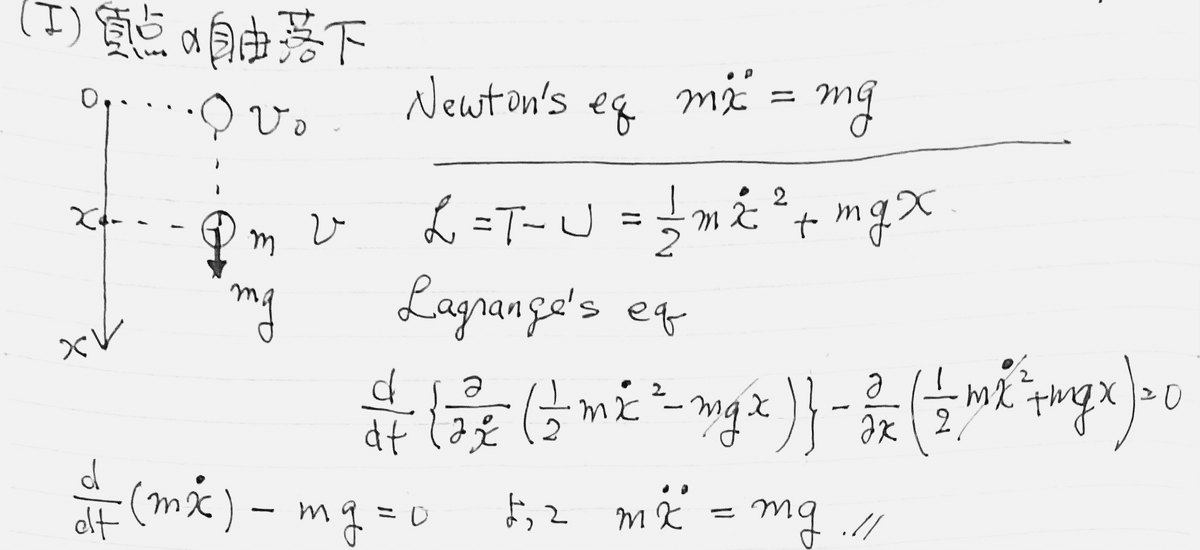
２ 単振動　　$${f=1 （  x  ）}$$

３ 放物運動　　$${f=2 （  x , y  ）}$$

４ 単振り子　　$${f=2 （  r , \theta  ）}$$だが、$${r=l}$$なので実は$${f=1}$$である。

５ 惑星の運動　　$${f=2 （  r , θ  ）}$$

　$${\begin{bmatrix}v_r\\v_\theta\end{bmatrix}}$$、$${\begin{bmatrix}a_r\\a_\theta\end{bmatrix}}$$の導出は、速度､加速度ベクトルの極座標表示を参照。
$${Lagrangean}$$の方法は$${T}$$の算出に$${v_r=\dot{r}}$$､$${v_\theta=r\dot{\theta}}$$を使うが$${a_r}$$､$${a_\theta}$$は使わない。しかし、結果として$${a_r=\ddot{r}-r\dot{\theta}^2}$$､$${a_\theta=2\dot{r}\dot{\theta}+r\ddot{\theta}}$$が現れる。

以上確かにこの方法で運動方程式が得られる。しかし今の私にはただブラックボックスをレシピ通りに操作しただけである。
これから少しずつ深みに入って箱の中身を覗いていくことにしよう。

追記
少しだけ理解が進んだ。一般化座標での式の導入を示す。

$${p_i}$$は$${p_i=\dfrac{\partial L}{\partial\dot{q_i} }}$$と再定義する。

　　　　　　　　　　　　　　　　　　　→ 力学､物理数学の目次へ