
小学算数の復習(小数)
小学算数の復習第二弾です。
近々生まれる息子と一緒に小学校の宿題を楽しくできる日を夢見て・・。
参考にした本
小学算数の解きかたが1冊でしっかりわかる本 小杉 拓也 (著)

第一弾(四則演算)編はこちら
小数の足し算・引き算
小数の足し算・引き算は何ら難しいことはありません。
小数点の位置を揃えて計算する、あとは整数の計算問題と何ら変わりません。


小数のかけ算
ステップ1)右側にそろえて計算する
一方小数のかけ算では、「右側にそろえる」のがルールになります。
小数点でそろえる必要はありません。

いったん小数点を無視して普通に計算します。

ステップ2)小数点を戻す
最後に小数点を戻してあげます。小数点の右側の数字が3つであったならば、小数点3つ分を計算の結果に戻してあげればよいのです。

小数点の位置が不安なら念のため検算してもいいかもしれませんね。
2.72×1.5はだいたい 3×1とか3×2くらい・・
3×1=3、3×2=6なので
小数点の位置は408.0でも40.80でもなく4.080!
となるわけです。
なぜかけ算は小数点を合わせる必要がないのか?
足し算・引き算は小数点を合わせて計算していたのに、かけ算はなぜ小数点を無視して計算できるのか、という問いに答えられますか?
足し算・引き算とかけ算はそもそも計算のプロセスが違うため、小数点を合わせて計算しても意味がないんです。
小数の掛け算では、小数点を左右に動かして計算します。
①「小数×小数」の掛け算は、掛けられる数と掛ける数に10、100、1000などを掛け、「整数×整数」に直して計算
②掛けた数字と同じ数で割って「小数×小数」の計算結果に戻す。


ちなみに小数点を合わせて計算したところで、この方法を使うと計算の結果は変わらなくなります。
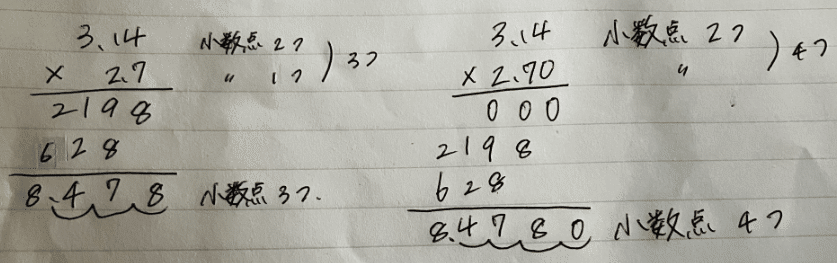
変わらないのであれば初めから小数点を合わせて計算する必要ありませんよね。だからかけ算については小数点をいったん無視して計算できるわけです。
小数点が動く仕組みがわからないという方は、この記事の最後に「小数点が動くルール」について解説していますのでそちらを参考になさってください。
小数点のダンス
小数点を動かして計算する方法の別バージョン。
ややこしい計算を簡単にする方法です。


この「ダンス」を分解すると、
かけられる数(2800)を100で割る
掛ける数(0.06)に100をかける
ということになります。
どういうことかというと、以下の仕組みを使っています。

1000×1、100×10、10×100、1×1000 掛ける数、掛けられる数に
同じ数をかけたり割ったりして式を変化させています。
どれも答えは同じになりますよね。
この要領で小数点のダンスも理解できると思います。
割合の問題もスムーズに解けるようになる!
この方法を使うと割合の問題もスムーズに解けるようになります。
6000円の3%は?
6000×0.03
=60×3 #小数点のダンスを利用
=180
180円 小数の割り算
小数の割り算のポイント
小数の割り算に移る前に、次のことを理解していただきたいと思います。
それは割る数と割られる数に同じ数字をかけると商は変わらない。
ということです。

小数の割り算のステップ
小数の割り算は
①割る数を整数にする。
(今回は割る数を10倍しているので、割られる数も10倍します。
そうすれば商は変わりませんね。)
②整数の割り算と同じ要領で計算する。
③小数点をつける。小数点は割られる数の真上につける。

小数点は割られる数の真上につけるが基本です。
なんで真上につけるの?という答えを自分なりに考えてみました。
「一度整数として普通に計算した後、小数点を戻す」のでつまりこういうことかと。

あまりのある割り算
あまりのある割り算に移る前にまず「あまり」とは何ぞやということを復習しておきましょう。
あまりとは、割り算をして割り切れずにあまった数です。
17個のあめ玉を5個ずつ袋に入れていくと3袋できて2つ余りますね。
このあまった2つが余りです。
あまりは必ず"割る数>あまり"になります。

こちらも基本的には小数点の割り算とやり方は同じですが、一つ違うことがあります。それはあまりの小数点のつけ方です。
あまりの小数点は、小数点を動かす前の小数点の位置と同じになります。

少しややこしいですね。
しかしここであまりを0.2ではなく2にしてしまうと少々不具合が生じます。
1.7を0.5で割ると0.5が3つできますね。
そのあまりを2にしてしまうとあまりがめちゃくちゃ多くなってしまうのです!!

なぜこんなことになるかというと、計算する際割る数を整数にするために、割る数・割られる数に×10をしています。 (1.7÷0.5 → 17÷5)
「割る数と割られる数に同じ数字をかけると商は変わらない」ということから(小数の割り算のポイント参照)商が「3」であることは当然問題ないはずです。
しかしあまりに関しては、そのまま小数点をおろしてしまうと10倍した数になってしまうのです。
したがって、正しい余りを求めるためには元の単位に戻す必要があるため、小数点をおろすときには元の数からおろしてくる必要があるのです。
小数の不思議
かける数が1以下だと、積は小さくなる。
わる数が1以下だと、商は大きくなる のはなぜか?
小学校の時、小数を初めて習ったとき不思議に思ったものです。
かけるとわるの本質がわかっていれば答えは簡単です。
まずかけるとわるの意味をおさらいしましょう。
かける
「かける」というのは… 10×2:「10が2個あったら」という意味です。 ○○○○○○○○○○ ○○○○○○○○○○=20
わる
「わる」というのは… 10÷2:「10の中に2はいくつあるか」
○○ ○○ ○○ ○○ ○○=5
または:「10が2個に相当するものは」という意味です。
(○○○○○)(○○○○○)=5
小数
では小数です。 小数0.5は、分数でいうと1/2のことです。 つまり1に満たないということですね。
10×0.5 (10×1/2)
これは「10が1/2個しかなかったら」つまり「半分だったら」という意味です。 だから当然数は小さくなります。○○○○○○○○○○=5
10÷0.5 (10÷1/2)
「10の中に1/2はいくつあるか」という意味で 10の中に1は10個だから、1/2は20個あります。 数が増えます。 ◐◐◐◐◐◐◐◐◐◐=20
出典:https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q103284582:
小数点が動くルールを理解する

ある数に10を1回掛けると、小数点が右に1桁動きます。
25×10=250
2.5×10=25
同じように、
2.5に10を2回掛けると、2.5×100=250で小数点が右に2桁動き、
2.5に10を3回掛けると、2.5×1000=2500で小数点が右に3桁動きます。
これらをまとめると、
ある数に10をN回掛けると、小数点が右にN桁動くとわかるでしょう。
逆に、
2.5を10で1回割ると、2.5÷10=0.25
2.5を10で2回割ると、2.5÷100=0.025
2.5を10で3回割ると、2.5÷1000=0.0025
です。これらをまとめると、
ある数を10でN回割ると、小数点が左にN桁動くとわかるでしょう。
