見出し画像
Photo by ピエール＝オーギュスト・ルノワール / メトロポリタン美術館

QAP.10：「DQM：Discrete Quadratic Models」の基本【量子コンピュータ/アニーリング@Python/D-Wave】

fz5050

【はじめに】

※再掲
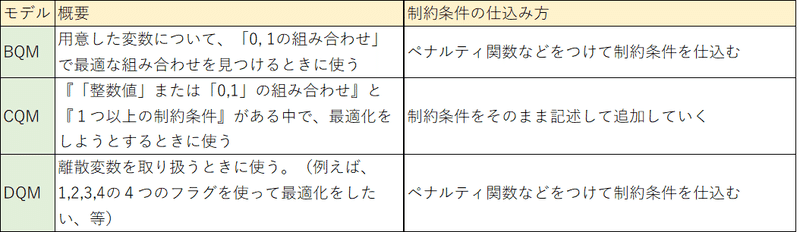
「D-Wave（Ocean SDK）」では、計算させたい問題の種類にあわせて、いい感じに取り扱ってくれる「Model（計算モデルオブジェクト）」を用意している。大きく分けて「３つ」ある。

・BQM：Binary Quadratic Models
・CQM：Constrained Quadratic Models
・DQM：Discrete Quadratic Models

今回は「DQM：Discrete Quadratic Models」について。

【ＤＱＭ概要】

公式ドキュメントによる説明と想定している数式は以下の参照。

ざっくりいうと

「何かの値を小さくしたい/大きくしたい」という「目的はない」が、
「ＸＸＸという制約条件」をみたすいい感じの組み合わせを見つけたい

といった状況で、離散値を取り扱いたい時に使える手段の一つ。

例えば、
　・グラフ彩色問題（４色問題）※何色を塗るかのフラグが離散値相当
　・従業員のライン配置問題　※どの配置場所を示すフラグが離散値相当
という問題など。

■DQMの変数の考え方

結論から言うと、ＤＱＭの変数は

[ 複数の0/1のバイナリ変数に係数がついている ]　＋　[ OneHot制約 ]

というもの。例えばDQMで「変数：x_0」を用意した場合、イメージ図は以下のような感じになる。

※イメージ図：「離散値：1,3,8,22」のいずれかをとる「変数：x_0」

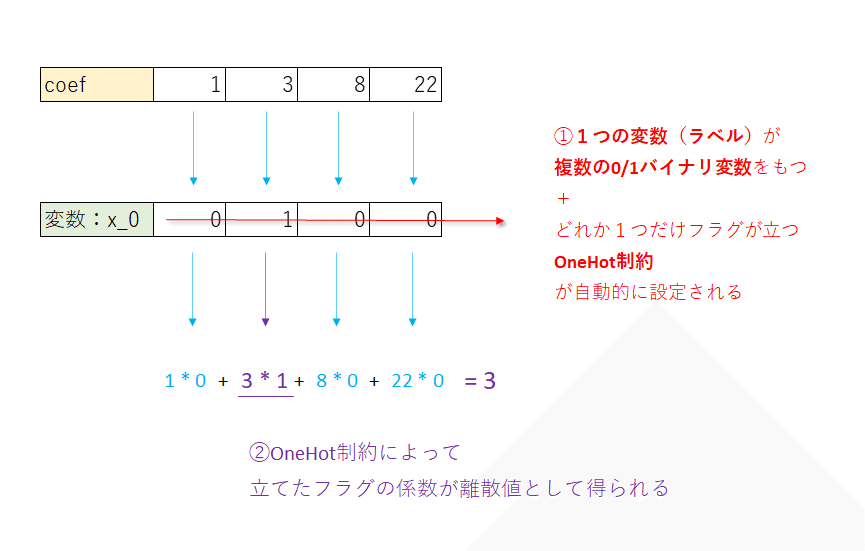
また「１つの変数（ラベル）が複数の変数を持つ仕組み」のため、量子アニーリングによる計算結果では、「どの位置のフラグが立ったかの値を示す仕様」になっている。

※計算後に返ってくる値のイメージ

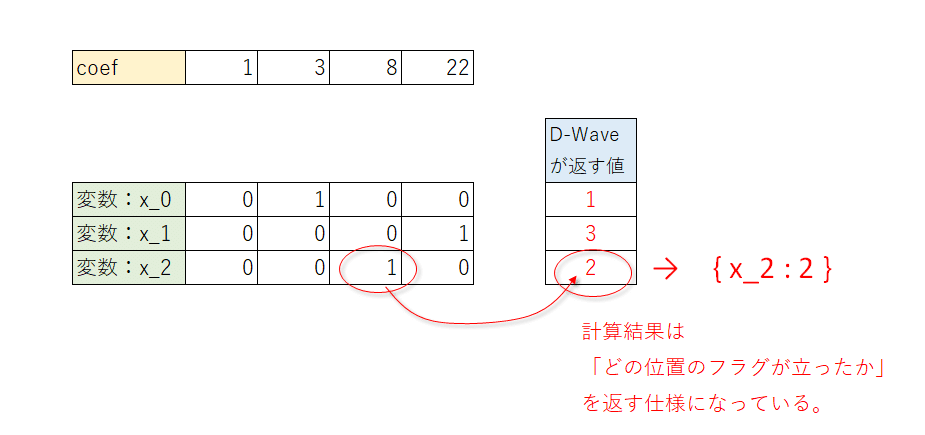
以上を踏まえつつ、例題を通してDQMの基本的な使い方をざっとまとめていく。

【例題】：東北６県の４色問題（D-Wave/DQM版）

問題：
東北６県について、隣接した県には同じ色を塗らないようにしつつ、できるだけ少ない色で塗り分けよう。

※この問題は「Fixstars Amplify」側でやった「例題：東北６県の４色問題」と同じもの。

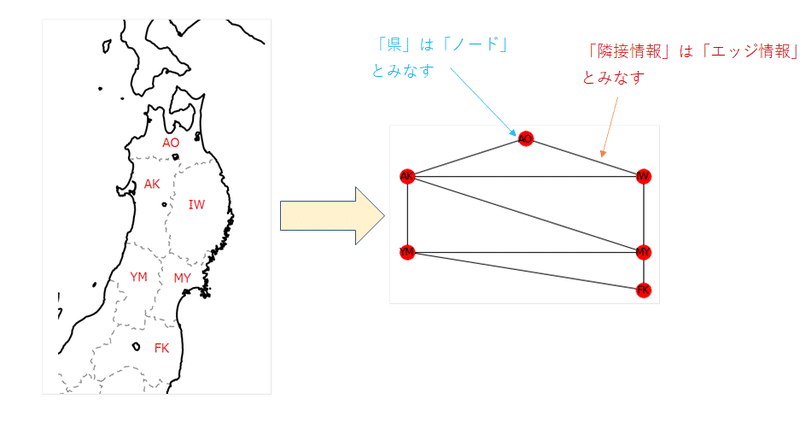
「考え方」も同様に「県をノード」、「隣接情報をエッジ」とした「グラフ理論：Graph theory」と考えていく。

【１】ライブラリのインストール

#ライブラリのインストール
!pip install dwave-ocean-sdk

（※再掲：ネット上を検索すると「dwave-system」というよく似たライブラリも出てくるので困惑するかもしれないが、「dwave-ocean-sdk」の「pip」時に一緒に入るので気にしなくてよい。）

【２】トークン設定

※再掲：
トークンを使ったD-Waveへのアクセスについては以下の通り

上記ドキュメント記載の通り、本来はアクセストークン漏洩防止など、セキュリティの観点から「コンフィグファイル」や「環境変数」に仕込む。

【注意】
今回は簡単なプログラムをちょっと試してみるだけなので、「Samplerオブジェクトに仕込む」というやり方で手抜きをしている。

リリースアプリ、実運用ではSamplerへのトークン埋め込みはしないこと。

■トークン設定

# Sampler埋め込み用トークン（本番では行わないこと）
# 各自登録して取得したアクセストークンを指定する
MY_DWAVE_TOKEN = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"

トークンを使った接続確認として、使用可能なSolver情報を出力してみる。

from dwave.cloud import Client

# トークンを使った接続確認
# 使用可能なSolver情報を出力する
client = Client.from_config(token=MY_DWAVE_TOKEN)
print(client.get_solvers())

【実行結果例】
[BQMSolver(id='hybrid_binary_quadratic_model_version2'), DQMSolver(id='hybrid_discrete_quadratic_model_version1'), CQMSolver(id='hybrid_constrained_quadratic_model_version1'), StructuredSolver(id='DW_2000Q_6'), StructuredSolver(id='Advantage_system4.1')]

【３】サンプルデータについて

「東北６県の隣接データ」を用意する。これも「Fixstars Amplify」の時と同じように「隣接リスト（adjacency list）」で作る。

※adjacency listについて

■「adjacency list」ファイルとして書き出し

text = '''AO,IW,AK
IW,AO,AK,MY
AK,AO,IW,YM,MY
YM,AK,MY,FK
MY,IW,AK,YM,FK
FK,YM,MY'''

with open("tohoku.adj",mode='w') as f:
    f.write(text)

■中身の確認(※colab上の操作想定)

!cat tohoku.adj

【実行結果】
AO,IW,AK
IW,AO,AK,MY
AK,AO,IW,YM,MY
YM,AK,MY,FK
MY,IW,AK,YM,FK
FK,YM,MY

▲「adjacency list」形式のファイルが出来上がっている

■作成したadjlistファイルを読み込んでデータ確認

import networkx as nx

# adjlistファイルを読み込む
G = nx.read_adjlist('tohoku.adj', delimiter = ',')

# ノードの取り出し（県名ラベル相当）
states = G.nodes
print(states)


# エッジ取得（隣接ペア）
borders = G.edges
print(borders)

【ここまでの実行結果例】
NodeView(('AO', 'IW', 'AK', 'MY', 'YM', 'FK'))
EdgeView([('AO', 'IW'), ('AO', 'AK'), ('IW', 'AK'), ('IW', 'MY'), ('AK', 'YM'), ('AK', 'MY'), ('MY', 'YM'), ('MY', 'FK'), ('YM', 'FK')])

▲ 「ノード情報(県ラベル)」と「隣接情報(エッジ情報)」として読み込まれている。


■参考：隣接状況の可視化

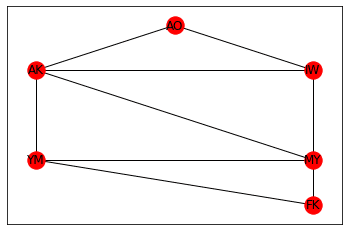
参考までに読み込んだデータをグラフとしてColab上で表示してみると次のようになる。

%matplotlib inline
import matplotlib.pyplot as plt

#描画用posデータ作成
pos_data = {
    'AO':(0.5, 2),
    'IW':(1, 1.5),
    'AK':(0, 1.5),
    'MY':(1, 0.5),
    'YM':(0, 0.5),
    'FK':(1, 0),
}

nx.draw_networkx(G,pos=pos_data, node_color="r")
plt.show()

【実行結果例】

【４】DQMの生成と変数用意

（ i ）まずは「DQMオブジェクト」を作成する。

import dimod


# DQMオブジェクトの作成
dqm = dimod.DiscreteQuadraticModel()

※DQMオブジェクトの使い方詳細は以下参照


（ ii ）次に変数を用意する。

DQMを使う場合は「add_variable()」で「変数名（ラベル）」と「必要なバイナリ変数の数」を設定する。

※「add_variable()」

■ノード（県名ラベル）ごとに４つの変数を作成する

# 4色分の色番号
# ※個々の変数にアクセスしやすいようにそのまま0,1,2,3を割り振りしている
colors = [0, 1, 2, 3]

# ラベル１つに対し、４つ分のbinary変数を生成
for state in states:
  label_name = dqm.add_variable(len(colors), label=state)
  # ラベル名, 生成した各変数の「係数」の値、変数の総数
  print(label_name, dqm.get_linear(state), dqm.num_cases(label_name))


# セットされた変数ラベル出力
print(dqm.variables)

【ここまでの実行結果】
AO [0. 0. 0. 0.] 4  　# ラベル：AO、各係数「0,0,0,0」、変数の総数４
IW [0. 0. 0. 0.] 4
AK [0. 0. 0. 0.] 4
MY [0. 0. 0. 0.] 4
YM [0. 0. 0. 0.] 4
FK [0. 0. 0. 0.] 4

Variables(['AO', 'IW', 'AK', 'MY', 'YM', 'FK'])

▲作成した「DQM」内に「ラベル」とそれぞれに「４つの変数」が生成されている。

なお、DQMで生成される変数は裏で次のような設定が仕込まれる

・「ラベル毎に生成される変数群」で「OneHot制約が自動設定」される
・「各変数の係数は０」で設定される

＜補足＞

設定状況の確認に使った「get_linear()」と「num_cases()」は以下参照。

※「get_linear()」：指定したラベル名が保有する「変数群の係数」を取得する

（例）「ラベル：IW」が持つ変数群の係数を出力する

dqm.get_linear("IW")
# array([0., 0., 0., 0.]) ※numpy.ndarrayで返ってくる


※「num_cases()」：ラベルを指定すると、そのラベルが保有する変数群の数を取得する。ラベル指定なしだと、内部で生成された変数の総数を取得。

（例）「dqm全体での変数の総数」と「ラベルAOの保有する変数の数」を出力する

# 生成したdqm全体での変数の総数
dqm.num_cases() # 今回は「24」（東北６県×４変数＝２４）

# ラベルAOが保有する変数の数
dqm.num_cases("AO") # 4

見た目的にはDQMに目的関数はないような感じになっているが、ここまでの変数作成によって以下のような数式（エネルギー式）ができている。

■DQMの変数生成と数式のイメージ図

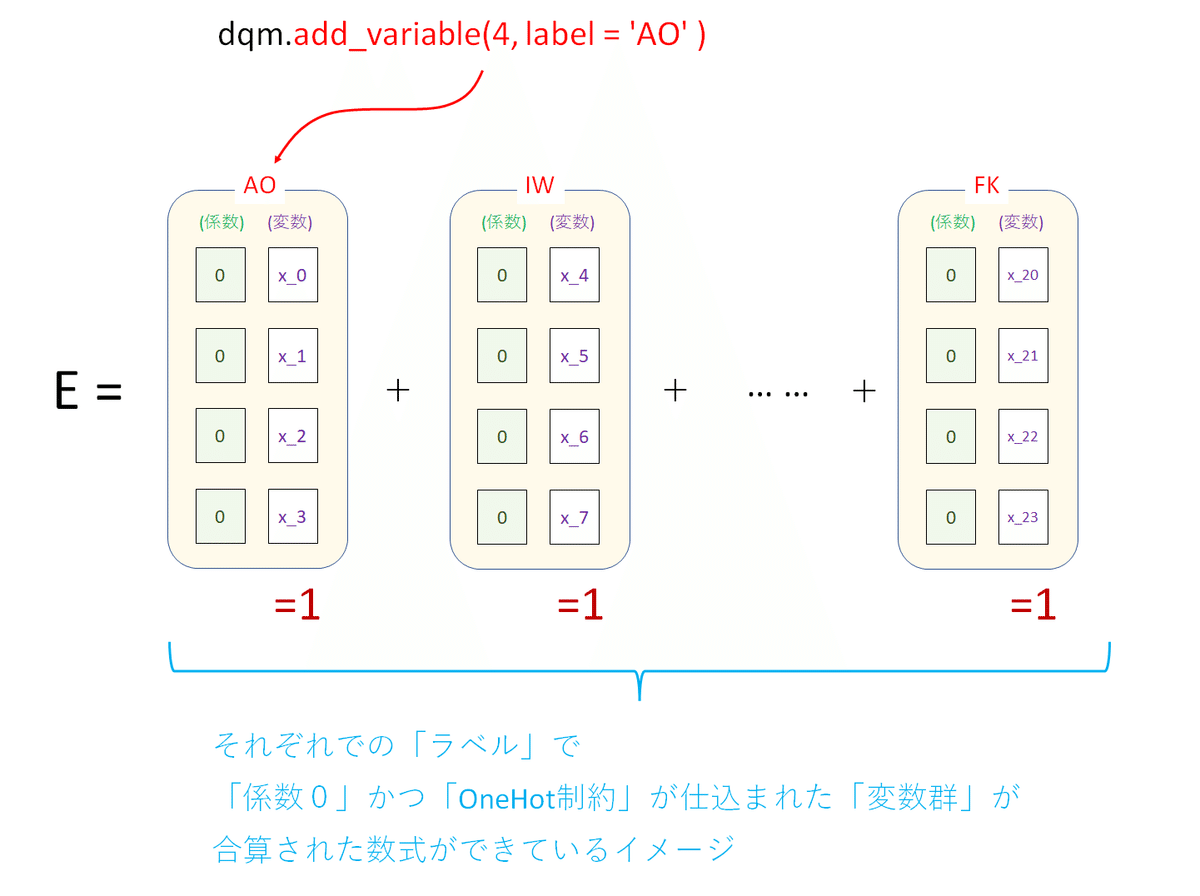
▲この時点では、係数が0なのでどんな変数の組み合わせでもＥ＝０となる

この後、「制約条件に対応する数式」をDQMに仕込んでいくことになる。

【５】DQMに制約条件を仕込む

DQMで制約条件を仕込むには、「制約条件に対応する数式（ペナルティ関数）」を考えることになる。

※再掲

▲「DQM」では「制約条件に対する数式」を制約条件として仕込む

■制約条件の2パターン

「DQM」では「制約条件に相当する数式」として「linearパターン」と「quadraticパターン」がある。

・linear：
　各変数を「足し算する形」で制約条件を表現する式の場合。

・quadratic：
　変数同士を「掛け算する形」で制約条件を表現する式の場合。

※linearとquadraticに対する制約条件の数式イメージ

今回の制約条件は、

「隣接県には同じ色を塗らない」
　→　隣接県同士で１を立てたフラグが、同じ色にあたるフラグなら
　　　ペナルティになる仕掛けを入れる。（隣接制約）

というもの。

※再掲
■イメージ図：ＡＯ（青森県）と隣接する県（ＩＷ：岩手、ＡＫ：秋田）

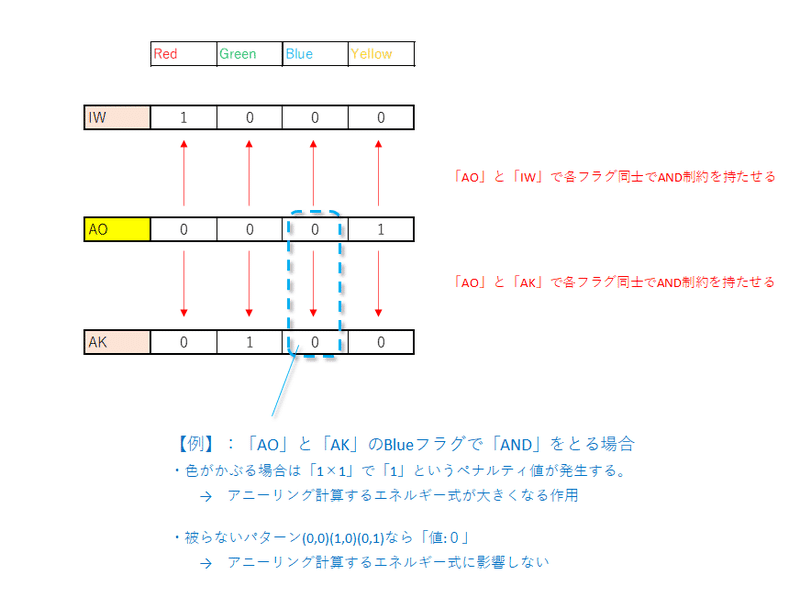
この「制約条件」は変数同士を「掛け算する形(AND制約)」で表現できる。すなわち「quadraticパターン」の制約条件である。

「quadraticパターンの設定」には「set_quadratic()」や「set_quadratic_case()」を使う。

※set_quadratic()

※set_quadratic_case()


今回は「set_quadratic()」を使ってみる。
まずは、「2つの変数を掛け算する形にした時に付ける係数」を用意する。

# 隣接県同士の各色同士の掛け算につける係数をdict型で用意
bias_dict = {(color, color): 1 for color in colors}
print(bias_dict)

【ここまでの実行結果】
{(0, 0): 1, (1, 1): 1, (2, 2): 1, (3, 3): 1}

▲隣接県の「0番目同士、1番目同士、、」の「変数を掛け算する時に付与する係数」は「１」という「dictオブジェクト」を作成している。

つぎに「quadraticパターン」として制約条件の数式をセットする。

# 隣接しているペアを取り出してループ
for state0, state1 in borders:
  dqm.set_quadratic(state0, state1, bias_dict)


# 確認用（セットされたquadratic部分の係数をあらためて確認）
for state0, state1 in borders:
  print(state0, state1, dqm.get_quadratic(state0, state1))

【ここまでの実行確認】
AO IW {(0, 0): 1.0, (1, 1): 1.0, (2, 2): 1.0, (3, 3): 1.0}
AO AK {(0, 0): 1.0, (1, 1): 1.0, (2, 2): 1.0, (3, 3): 1.0}
IW AK {(0, 0): 1.0, (1, 1): 1.0, (2, 2): 1.0, (3, 3): 1.0}
IW MY {(0, 0): 1.0, (1, 1): 1.0, (2, 2): 1.0, (3, 3): 1.0}
AK YM {(0, 0): 1.0, (1, 1): 1.0, (2, 2): 1.0, (3, 3): 1.0}
AK MY {(0, 0): 1.0, (1, 1): 1.0, (2, 2): 1.0, (3, 3): 1.0}
MY YM {(0, 0): 1.0, (1, 1): 1.0, (2, 2): 1.0, (3, 3): 1.0}
MY FK {(0, 0): 1.0, (1, 1): 1.0, (2, 2): 1.0, (3, 3): 1.0}
YM FK {(0, 0): 1.0, (1, 1): 1.0, (2, 2): 1.0, (3, 3): 1.0}

▲「隣接県情報（エッジ情報）」について、「同じ色同士のフラグ変数が両方１になる」と「値１がでる」ように「係数１」が設定されているのがわかる。

※作成されているエネルギー式のイメージ図

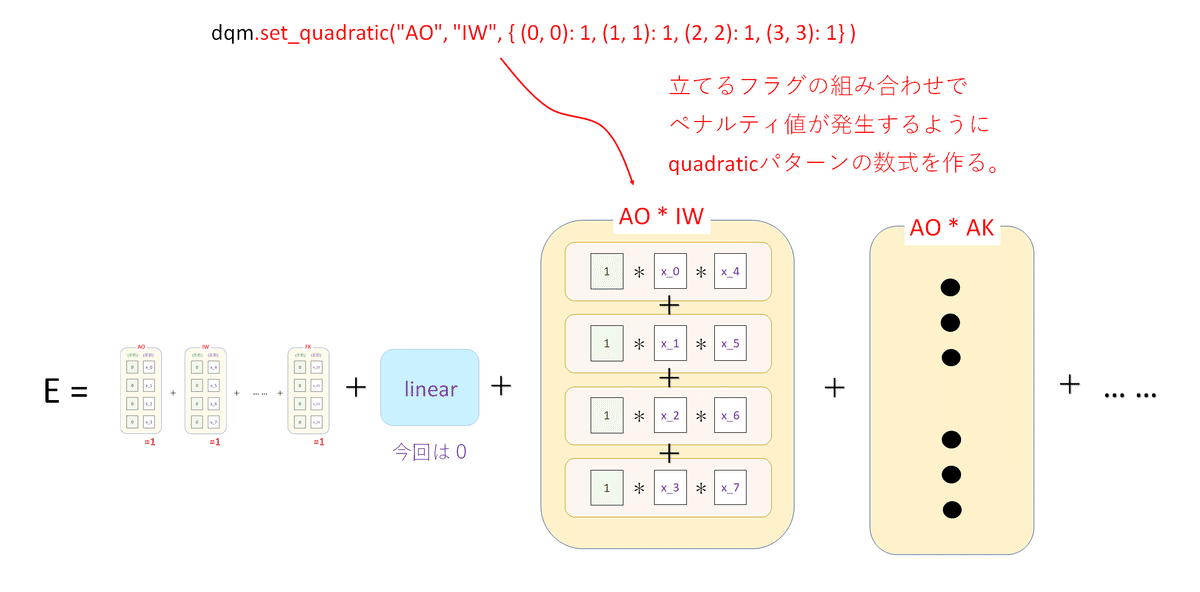
これで「隣接県には同じ色を塗らない」という制約条件の仕込みが完了した。

以上で、変数生成時に自動的に設定された「OneHot制約」、「同じ色を塗らない制約」の「2つの制約条件の設定」ができたので、あとはSampler経由で量子アニーリング計算をすればよい。

【６】Sampler経由で量子アニーリング計算する

※再掲：Samplerオブジェクト
「D-Wave（Ocean SDK）」では、「解きたい問題に対するパラメータを設定したModel」を「Samplerオブジェクト」に渡す。これは大きく分けて５つある。

「ＤQM」に対応する「Sampler」は「LeapHybridDQMSampler」である。

■LeapHybridDQMSampler

これを使って量子アニーリング計算をする

from dwave.system import LeapHybridDQMSampler


# トークンを仕込んだSamplerにmodelを投げ込んで計算する
sampler = LeapHybridDQMSampler(token=MY_DWAVE_TOKEN)
sampleset = sampler.sample_dqm(dqm, label='TOHOKU Map Coloring DQM')

【７】結果を確認する

「Sampler」経由で「D-Wave上のSolver」が計算した結果は「SampleSetオブジェクト」として返ってくる。

■SampleSetオブジェクトについて

※見やすいようにlist化して整形している

# list化して整形
print( list(sampleset.data()) )

【実行結果例】
[Sample(sample={'AO': 1, 'IW': 3, 'AK': 2, 'MY': 0, 'YM': 3, 'FK': 2}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 0, 'IW': 1, 'AK': 3, 'MY': 2, 'YM': 1, 'FK': 0}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 3, 'IW': 1, 'AK': 0, 'MY': 3, 'YM': 2, 'FK': 0}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 2, 'IW': 0, 'AK': 1, 'MY': 2, 'YM': 0, 'FK': 3}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 3, 'IW': 0, 'AK': 1, 'MY': 2, 'YM': 0, 'FK': 1}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 1, 'IW': 0, 'AK': 2, 'MY': 1, 'YM': 3, 'FK': 2}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 2, 'IW': 3, 'AK': 1, 'MY': 2, 'YM': 3, 'FK': 1}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 0, 'IW': 3, 'AK': 1, 'MY': 0, 'YM': 3, 'FK': 1}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 2, 'IW': 1, 'AK': 0, 'MY': 2, 'YM': 1, 'FK': 3}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 1, 'IW': 2, 'AK': 0, 'MY': 1, 'YM': 2, 'FK': 3}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 1, 'IW': 0, 'AK': 3, 'MY': 2, 'YM': 0, 'FK': 3}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 3, 'IW': 2, 'AK': 0, 'MY': 1, 'YM': 3, 'FK': 2}, energy=0.0, num_occurrences=1)]

▲塗分けられているっぽい結果（energy=0の組み合わせ）が出ているが、よくわからないので可視化する。

【８】可視化して確認する

今回も「Maplotlib＋networkx」で描画して確認してみる。

いくつか答えがあるので「SampleSet.first」で１つ取得した答えを描画してみる。

※「変数：pos_data」は「【３】の参考」のプログラムの内容を流用。

my_nx_other_param ={
    "node_color":list(sampleset.first.sample.values()),
    "with_labels":True,
    "cmap":plt.cm.rainbow,
    "node_size":400
}

nx.draw(G, 
        pos=pos_data,
        **my_nx_other_param)

【実行結果例】

▲隣接県同士で色が同じにならないように塗分けられている

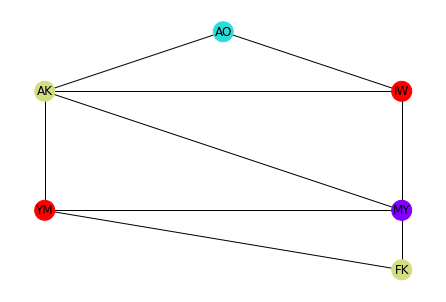
【９】全体コード

最後に全体コードを示しておく。

問題：
東北６県について、隣接した県には同じ色を塗らないようにしつつ、できるだけ少ない色で塗り分けよう。

【実行環境】
・D-Wave Leap　＋　Google Colab

■事前準備：ライブラリのインストール

#ライブラリのインストール
!pip install dwave-ocean-sdk

■ここからが全体コード

from dwave.cloud import Client
from dwave.system import LeapHybridDQMSampler

import dimod

%matplotlib inline
import matplotlib.pyplot as plt
import networkx as nx



# Sampler埋め込み用トークン（本番では行わないこと）
# 各自登録して取得したアクセストークンを指定する
MY_DWAVE_TOKEN = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX"


# トークンを使った接続確認
# 使用可能なSolver情報を出力する
client = Client.from_config(token=MY_DWAVE_TOKEN)
print(client.get_solvers())


# サンプルデータ作成
text = '''AO,IW,AK
IW,AO,AK,MY
AK,AO,IW,YM,MY
YM,AK,MY,FK
MY,IW,AK,YM,FK
FK,YM,MY'''

with open("tohoku.adj",mode='w') as f:
    f.write(text)


# 作成データファイル確認(colab上操作想定)
#!cat tohoku.adj


# adjlistファイルを読み込む
G = nx.read_adjlist('tohoku.adj', delimiter = ',')

# ノードの取り出し（県名ラベル相当）
states = G.nodes
#print(states)


# エッジ取得（隣接ペア）
borders = G.edges
#print(borders)



#描画用posデータ作成
pos_data = {
    'AO':(0.5, 2),
    'IW':(1, 1.5),
    'AK':(0, 1.5),
    'MY':(1, 0.5),
    'YM':(0, 0.5),
    'FK':(1, 0),
}

# 描画してノードとエッジの読み込み状況を確認
#nx.draw_networkx(G,pos=pos_data, node_color="r")
#plt.show()



# DQMオブジェクトの作成
dqm = dimod.DiscreteQuadraticModel()


# ノードごとに4つの変数を用意する
# 4色分の色番号
# ※個々の変数にアクセスしやすいようにそのまま0,1,2,3を割り振りしている
colors = [0, 1, 2, 3]

# ラベル１つに対し、４つ分のbinary変数を生成
for state in states:
  label_name = dqm.add_variable(len(colors), label=state)
  # ラベル名, 生成した各変数の「係数」の値、変数の総数
  #print(label_name, dqm.get_linear(state), dqm.num_cases(label_name))


# セットされた変数ラベル出力
#print(dqm.variables)


# 制約条件を設定する
# 隣接県同士の各色同士の掛け算につける係数をdict型で用意
bias_dict = {(color, color): 1 for color in colors}
#print(bias_dict)

# 隣接しているペアを取り出してループ
for state0, state1 in borders:
  dqm.set_quadratic(state0, state1, bias_dict)


# 確認用（セットされたquadratic部分の係数をあらためて確認）
#for state0, state1 in borders:
#  print(state0, state1, dqm.get_quadratic(state0, state1))



# トークンを仕込んだSamplerにmodelを投げ込んで計算する
sampler = LeapHybridDQMSampler(token=MY_DWAVE_TOKEN)
sampleset = sampler.sample_dqm(dqm, label='TOHOKU Map Coloring DQM')


# 結果の確認
# list化して整形
print( list(sampleset.data()) )

【実行結果例】
[Sample(sample={'AO': 1, 'IW': 3, 'AK': 2, 'MY': 0, 'YM': 3, 'FK': 2}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 0, 'IW': 1, 'AK': 3, 'MY': 2, 'YM': 1, 'FK': 0}, energy=0.0, num_occurrences=1),

… (略) …

Sample(sample={'AO': 1, 'IW': 0, 'AK': 3, 'MY': 2, 'YM': 0, 'FK': 3}, energy=0.0, num_occurrences=1),
Sample(sample={'AO': 3, 'IW': 2, 'AK': 0, 'MY': 1, 'YM': 3, 'FK': 2}, energy=0.0, num_occurrences=1)]

■結果を可視化
SampleSet.firstで取得されたもの１つだけ描画して確認してみる

my_nx_other_param ={
    "node_color":list(sampleset.first.sample.values()),
    "with_labels":True,
    "cmap":plt.cm.rainbow,
    "node_size":400
}

nx.draw(G, 
        pos=pos_data,
        **my_nx_other_param)
▲隣接県同士で色が同じにならないように塗分けられている

【補足】dwave-networkx

今回は「networkx」で作成したデータを読み込んで、DQMを作成して量子アニーリング計算を実施した。

再掲になるが、「networkxパッケージ」自体はグラフ・ネットワーク理論用向けに作られたものであり、「４色問題（グラフの彩色問題）」を解くアルゴリズムも搭載している。

「D-Wave」では「networkx」との間で、データのやり取りをしやすくするために「dwave-networkx」というパッケージを用意している。

これを使うことで、「networkxで読み込んだデータ」を「D-Waveの量子アニーリング計算」に直接渡して、「dwave-networkx」が対応している「グラフ理論の問題」を解かせることもできる。


いいなと思ったら応援しよう！

fz5050
もっと応援したいなと思っていただけた場合、よろしければサポートをおねがいします。いただいたサポートは活動費に使わせていただきます。