
SFCベースカレツキアンモデルの修正と拡張
おおよそ二万字に及んだ前回の「ストックフロー一貫カレツキアンモデル」ですが、記事の後半たる「 長期均衡・負債比率の内生化」が理論的に不十分でした。
ですので今回は、その訂正+拡張+長期均衡に関する新たな発見を書いてゆこうと思います。
「訂正箇所の説明→モデルの考察と拡張→今後の課題」という流れになっています。モデルの説明はもうやったのでここではしません。よろしければ前回の記事をご覧ください。
イントロ
さて実物モデルにおいて、ストックを内生化するのは非常に難しい事でした。京大の佐々木教授が分かりやすく理由を書いてるのでコピペしとくね♡
「カレツキアン・モデルにおいて資本ストックの蓄積を明示的に考えようとすると、 後述するように、雇用率(あるいは資本ストック・労働 供給比率)を内生変数にする必要がある。短期カレツ キアン・モデルでは,労働は企業の労働需要に応じて無制限に供給されると仮定されている。しかし、中期を考える場合、労働供給には制約があると考えるのが 自然である。すると,雇用率を内生変数にすればよい。しかし,そのためには変数の数を1つ増やす必要があり,これは微分方程式の数を 1 本増やすこ とにつながり,分析が複雑になってしまう。このような事情で,資本蓄積を明示的に考慮したカレツキアン・モデルは少ないのである」(佐々木:カレツキアンモデルにおける短期・中期・長期。2010)
だそうです。
しかしSFCベースモデルでは、バランスシートマトリクスとトランザクションマトリクスを使用する事で、そこまで無理なくストックを内生化できます。ただし、これは”量”の変化を明確に定義するわけではありません。比率の変化を定義する事で、間接的にストックを内生化していきます。
SFCベースカレツキアンモデル
元となるバランスシート&トランザクション・マトリクスは以下のとおりである。


では前回のモデルを流用すると共に、前提条件と仮定を明確にします。
経済は企業、家計、銀行の3主体で構成され、銀行は利潤を稼がず資金をアコモデートする存在と仮定し、家計は労働者階級と資本家階級を集計的に含んでいるとする。企業は成長最大化行動と、費用最小化行動を取り、生産関数はレオンチェフ型を採用する。加えて在庫投資は発生せず、需要対して弾性に生産がなされるとする
また経済は、常にケインジアン安定条件を満たしていると仮定する。↓
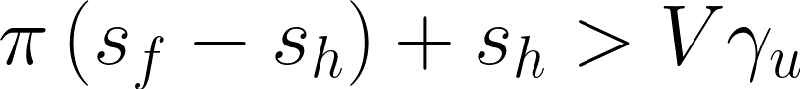
成長最大化条件と内部留保の定義
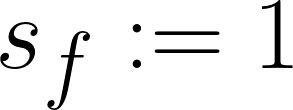

費用最小化条件
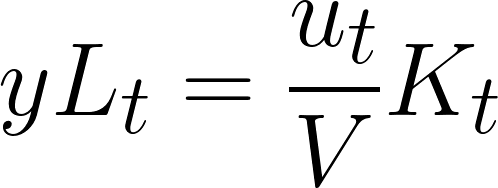
y=労働生産性、V=資本係数、t=時間
レオンチェフ型生産関数

これにて不明瞭だった部分を明確にできましたので、実際にモデルを拡張していきます
前回のモデルの復習です。上記の仮定とマトリクスより、貯蓄方程式は…

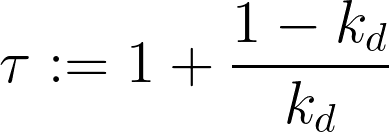
また同様にBhaduri&Marglin型投資関数を拡張し、ミンスキー的な視点を取り入れた投資方程式を使用する↓

よって短期均衡地点は…

ケインジアン安定条件が常に成立している場合、以下のように図示する事が出来る。

この時、負債・資本ストック比率(B/K=D/K=ℓ)は定数として扱っています。このような仮定は、せっかくSFCモデルをベースとしているのに、その特性をうまくいかせていません。
では負債・資本ストック比率を変数として扱うには、負債の変化と資本ストックの変化を明確にしなければなりません。
トランザクション・マトリクスより、負債の変化量は…
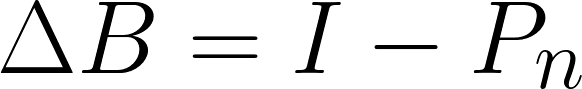
次に資本ストックの変化量は…
![]()
したがって、負債変化量は以下のようになる
![]()
では短期均衡が常に満たされているとし、時間を明確に書いた形にすると、変化率は以下のように書けます。

この式を書き換えると以下のようになります。

これにて負債変化率を、負債・資本ストック比率の関数として記述できました。
次に負債・資本ストック比率の変化率は以下のような関係を持ちます(対数変化率で近似した関係性です)

では以上の関係より、負債変化率と資本ストック変化率が同値になる点が均衡地点である事が分かりますね。そして負債の変化率も資本ストック変化率も負債・資本ストック比の関数として記述できる(短期均衡が常に達成されているという条件の下)
よって上記の関係に、導出した二つの式を代入すれば…

これにより、変化率を示せました。文字だけではわかりずらいので、図示してみましょう。
パターン①

パターン②

パターン③

負債・資本ストック比率が安定するパターンは大体こんな形をしています。
場合によっては均衡点が存在せず、発散してしまう場合もありますが、今回は考慮しません。
修正版:負債主導型経済・負債抑制型経済
利率が経済に与える影響は、前回の記事でも書いた通り、非常に複雑です。
負債と成長率に正の関係性が見いだせる場合、それは負債主導型経済と言われます。逆であれば負債抑制型経済です。
正の関係がみられるのは、パターン①とパターン②のグラフですね。気を付けなければならない事がありまして、①・②のような形状をしている=負債主導型ではないです。実際は投資関数にある利払いのパラーメターがどれだけ強いかで変わります、長期的に利子率が増加&利払い反応性が強い時、g(l)の傾きは負になってしまい、負債抑制型経済に移行します。
負債主導型の場合は、借り入れに対して意欲的ですから、負債成長率も正の値を取ります。場合によっては、パターン②の様に負債比率が上昇しても意欲的に債務を更に積み上げる場合もあり得ます。
パターン①は負債の増加に伴って成長率が大幅に拡大するものの、企業は利払い負担から、さらなる融資の増加に消極的になり、負債増加率は減少していきます。結果的にいずれ成長率と負債増加率が均衡し、負債・資本ストック比率が安定するでしょう。
パターン②は、①同様に負債が資本蓄積を大きく押し上げます。さらに負債資本ストック比率の増加に企業は楽観的で、さらなる借り入れを意欲的に受け入れます。これは負債・資本ストック比率を大幅に上昇させ、投資が活発化します。しかしいずれ負債の増加と資本蓄積が見合わなくなり、投資は落ち着きます。(このパターンが現れるには、企業が株式市場での評価にある程度反応する必要があります)
パターン③は、少し直観的には分かりにくいケースかもしれません。このようなパターンは株式市場への反応度が非常に低い時に見られます。ですので家計の貯蓄性向によってもたらされる負債の増加(=預金の増加)を非常にネガティブに評価している。と言えるでしょう。本来負債の増加は、結果的に株式市場を盛り上げ企業の市場価値を高めますが、株式市場を見ていない故にこの様な現象が起きます。
静学比較:利子率が負債に与える長期的影響
パターン①型

パターン②型
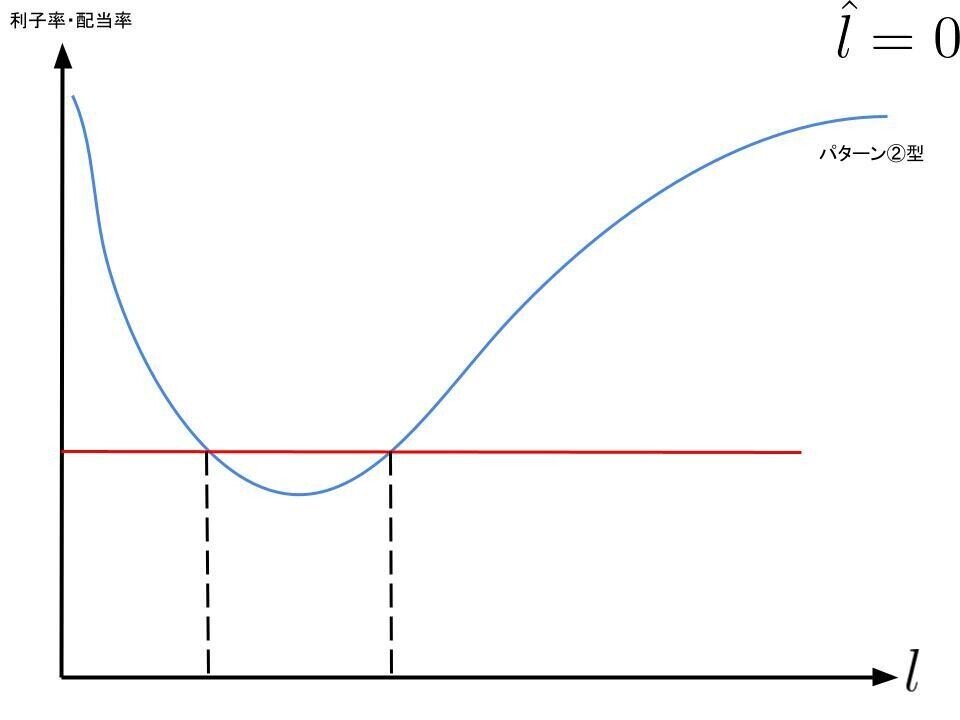
パターン3型

長期的な調整が終了していると仮定し、利子率を変数とすると、利子率と負債・資本ストック比率の均衡点の集合を観察できます。式は複雑な陰関数となってしまうため簡単には解けません。(グラフにするのは簡単だけど)
はい、まあ見りゃわかるでしょ。おわり!
修正版:ミンスキー体制・スタインドル体制
稼働率が負債・資本ストック比率を上昇させるような経済状態、つまりは稼働率の変化率が負債・資本ストック比率に正の影響を与える事をミンスキー体制といい。逆に稼働率の変化が負債・資本ストック比率をへらすような状態をスタインドル体制と言います。
これは前回も書いたように、負債・資本ストックの式を稼働率で偏微分した時の正・負で判断できます。

では、これ↑を稼働率で偏微分しましょう。

偏微分が負になるのは負債・資本ストック比が比較的大きい場合になります。
うん…これもそんなにいう事ないかな…
ちなみにね、負債・資本ストック比率の式を三次元空間上に図示したら結構綺麗だったよ

PC曲線、インフレーションバリア、実物制約
SFCへと拡張したことにより、実物モデルの時のように貯蓄性向の逆数をかけるだけでは成長率を利潤率に変換できなくなってしまいました。
これによって有効需要曲線(ED曲線)が消滅してしまいます。しかしながらPC曲線は保持されます。なぜならこれには貯蓄性向が関わってこないからです。

はい、ですので利潤と稼働率の関係性は単純な線形になります。
金融側面を導入しても実物的な側面から導き出せる関係性は消えない、というのは中々面白いですね。
さてさて、ネオケインジアンモデルで特徴的だった「インフレーションバリア」がSFCベースカレツキアンモデルでは非常に便利な分析ツールになります。(インフレーションバリアの詳しい事は実物モデルの解説に乗っけてます)
なぜなら多数のパラメーターが導入されたことにより、実質賃金率と成長率を簡単に結びつける事がミスリーディングになってしまいます。しかしインフレーションバリアは、経済が到達できる限界の実質賃金率と利潤率を示しているだけであり、それすなわち”実物制約”を表しているのです。
成長率、稼働率、利潤率、実質賃金率の同時均衡

画像内にも注釈しましたけど、実質賃金と成長率は変動が激しいです。
前回の記事にも書きましたが、賃金が成長率を押し上げる「賃金主導型成長」への経路は場合によっては閉じてしまいます。
うん、まあ大方満足。前の記事に基本的な事書いてるし…
さらなる拡張、内生化、ルーカス批判とか
ちなみにですね、負債・資本ストック比率が安定していても、それは真の意味での長期均衡ではないんですよね。
なぜなら成長率も負債増加率も正の値にいるからです。本来であれば、これらの変化率も長期的には零にならなければ長期均衡とは言えません。
これを実現する方法としては「資本係数」の内生化が必要になります。このモデルでは有形資産を固定と仮定しているので、資本ストックの増加は本質的には負債の増加でしかありません。生産に使用される資産とは「有形資産(=Vf)」です。これを分析するのは難しい…………
まあこれは一財&政府なし&閉鎖体系モデルの限界でしょうね。
加えてこれまでの議論は流動性選好、貯蓄性向、利子率の長期的変化を考慮しておらず、その意味で各種主体の行動方程式は不十分な形のままです。これらを内生化する必要がありますが、その手法はルーカス批判を考慮した形にしなければならないでしょう。
個人的には「効用関数を部分的に適用し貯蓄性向を内生化」「流動性選好を利子率の関数として内生化」等々いろいろ考えていますが、難しいです。
上記のやり方は「主体の行動を効用関数で基礎づける事で内生化する」という新古典派的な手法ですね。
ポストケインジアン的な手法としては「純利益率を雇用率・稼働率の関数として描き、産業予備軍効果とフィリップスカーブを導入する」なんてのもあります。
どのみち明確に労働市場を定義したり、主体の行動原理を基礎づける必要があるので、簡単な話にはなりません。
数学的に非常に高度な操作をする必要が出てきますから、僕の数学レベルではね……厳しいかな…
っあ!!!SFCベースカレツキアンモデルのサーベイを僕と一緒に書きたい人いませんか!?!?!?一人ではきつくて……
募集中です★
