ポストケインジアンの動学モデル:古典、マルクス、ケインズの融合
面倒だから最近サムネ毎回MMTの表紙にしてる。こたつです。
なんか勉強するほどに、いかに自分が無知で馬鹿なのかを思い知らされる。
はぁ~
さて、今日も今日とて独り言記事です。
今回メインで紹介してゆくのは、俗に「カレツキアンモデル」と呼ばれるものになります。
カレツキアン
カレツキアンはPK一派の一つで、ほとんどの他勢力と親和的な態度を取る派閥でもあります。
彼らの理論は、古典的でマルクス的でケインズ的です。
どういった意味で古典的か?と言いますと、経済を労働者と資本家に分ける手法や、実物ベースで分析する点において古典的です。
マルクス的な部分は、賃金・利潤フロンティア(インフレーションバリア)と階層闘争型インフレーション理論を支持する所でしょう。(これはスラッファも含む)
ケインズ的特徴は、倹約の逆説が支持される事ですね。
彼らのモデルの一番の特徴は「コストのパラドックス」と「貯蓄から完璧に独立した投資関数」の存在にあるでしょう。
ではこの記事では、カレツキアンモデルを大まかに紹介しつつ、長期(短期の世界での)分析と経済の均衡点を考察します。
短期と長期
よく経済学で「短期」や「長期」という言葉が使われる時、それは時間を意味しません。条件が達成されているか否か?で期間を区別します。
短期の定義:資本ストックは固定・完成された期待
長期の定義:資本ストックの変化・技術進歩
今回扱うのは短期のみになります。
資本ストックの変化を考慮し始めると、大学レベルの数学を使う必要が出てきてしまい。私が理解できないからです(笑)
ですが、軽く長期におけるPKの世界観を紹介しておきましょう。
★自然成長率は内生的に決定される
一般的に自然成長率は人口成長率と技術革新によって起こされる、外生的要因として処理されます。PK派にとって自然成長率は長期的な需要の状態で決定される内生的なパラーメーターであり、独立しません。
なぜなら需要の高い+労働分配の多い経済では、人口成長率が高まる事も高い資本蓄積と共に技術進歩の促進も誘発されるからです。
経済全体の需要からくる圧力が、将来的な技術進歩と成長水準に影響を与えるのであって、外生的に取ってつけたように与えられるわけではない。(詳しいことはVerdoorn's lawとか調べれは出てくるで♡)
この様に一貫して需要→供給という因果を描くのがPKの特徴ですね。
モデルの前提と分析範囲
では見出しの通り、今回使用するモデルの前提と分析の範囲を紹介します。
・2階級、1種労働、1財モデル
・ターゲット・リターンプライジングの採用
・The Bhaduri&Marglin型投資関数の採用
・通常稼働率自体の内生化
・数量&価格調整(期待利潤率が固定)
・インフレーションバリア+番外的に階級闘争型インフレーションの分析
・限定的なSFCモデルへの拡張、ミンスキー的負債成長の分析(後編になるかも)
実物的ポスト・カレツキアンモデル
最も一般的なモデルである「ポスト・カレツキアンモデル」を紹介します。
2階級1財のマクロモデルで「分配、成長、利潤、稼働率」を分析する事に非常に特化したモデルと言えるでしょう。
一部の人は「実物的とはどういうこと?」と疑問に思われるでしょう。
金融側面や貨幣の役割を非常に強調するポストケインジアンが、なぜこのような実物モデルを使用したのでしょうか?
それは単に実物面と金融面の混同があった事も原因ではありますが、メインの理由はおそらくその複雑性からくるものでしょう。
金融側面を”正しく”導入するには、ファイナンスされた資本金(そしてそれは多くの場合銀行からの借り入れという形を取る)が投資や賃金、株の発行を通して、どのように家計に渡り(単に家計に現金が入るわけではなく家計の預金になる、これは銀行の金融債務と計上される)消費の決定、株式の購入が行われるのかを”ストック&フロー”が一貫した形で記述する必要があります。その都合上一般的にフローのみで記述する国民経済計算では捨象されている銀行部門を明示的に導入しなればなりません。
カレツキの言葉に代表されるように「経済学とはストックとフローを混在する学問である」それは主流派においては今も健在の問題ですが、PKにとっても昔はそうだったんです。
そのため過去ポストケインジアンでは金融側面を曖昧にした実物的モデルが使用されました。
金融側面は明示的に導入されていないとはいえ、カレツキアンモデルは十分に興味深い結果を見せてくれます。
ターゲットリターンプライジング
特定の利潤率が特定の稼働率で達成されるマージンを設定するタイプの価格設定です。(今回のような価格調整型モデルはターゲットリターン型の価格決定のみ意味を持ちます)
言葉の定義
V=資本係数、r=利潤率、P=価格水準、K=資本ストック、R=利潤量、A=単位コスト、Θ=コストマージン率、q=生産高(実質量)
まずは国民経済計算の視点から……
ある水準の生産高で欲求する利潤が達成されてほしいので、欲求利潤量は……
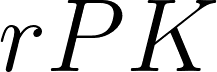
ではこれを稼働率と資本係数を使って、わざと複雑に書きましょう。
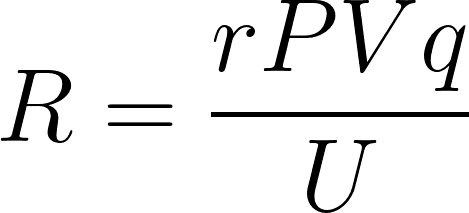
今度はサプライサイドの視点から……
サプライサイドから見た利潤量は以下のように表せられます
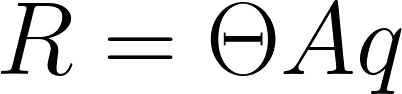
では国民経済計算から見た利潤量とサプライサイドから見た利潤量を連立方程式にして価格水準で解きましょう。すると……
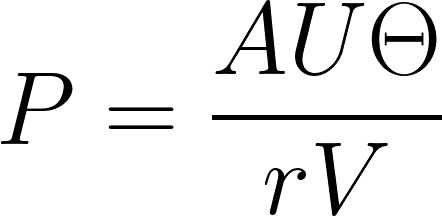
この様に価格が導出できましたので、これを今度は一般的なマークアップ型の価格式と連立方程式を組みましょう。
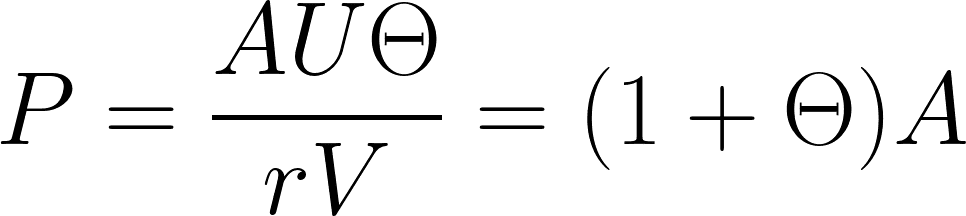
そして上記の式をマークアップ率(Θ)で解きましょう。
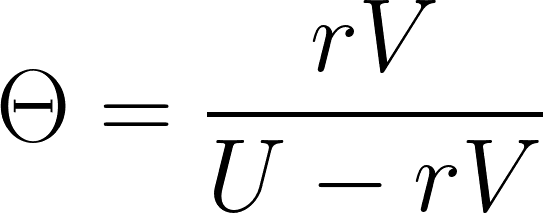
はい、導出完了です。
ちなみに書き忘れていたけど、この利潤率(r)も稼働率(U)もすべて「通常利潤率・稼働率」を意味します。本来は「rn」「Un」と書くべきなんだけど忘れてた。
一種労働の場合は粗利潤も純利潤も一緒になっちゃうからこれで終わり、もし間接労働を考慮するならもうちょっと複雑になる。
で一度マークアップが分かれば純利益率(π)もわかるので……
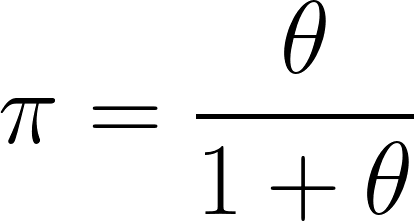
ですね。(Θが小文字になっちゃったけど気にすんな)
The Bhaduri&Marglin型投資関数
さてさて、ポスト・カレツキアンモデルの一番の特徴たる「 Bhaduri&Marglin型投資関数」の紹介といきましょう。
まずはポストケインジアン動学モデルの特徴を軽く……
主流派ではI=Sという事後的関係性から、効用に基づいた代表的個人の貯蓄が投資として表現され、投資は貯蓄から生まれるものとして処理されます。
しかし、PKは完璧に貯蓄関数から独立した投資関数を持ちます。
ケインズのアニマルスピリットを心理的な反応性パラメータとして導入し、資本家たちの”予測値”から投資が決定されます。
それがI>SもしくはI<Sという超短期不均衡を起こした後に、市場によって稼働率の調整をもってしてI=Sに修正され、結果的に資本家たちが受け取る実際の利潤量+生産高から、資本家は来期の予測値を修正し投資を調整します。
投資に影響を与える変数は何か?
主流派経済学において、IS=LMモデルに代表されるように、投資に影響を与えるのは「利子率」です。しかしポストケインジアンにおいて投資に景況を与える変数は「純利益率」と「稼働率」です。
これは実証研究からもある程度信憑性があります。企業にとって利子率は未来の投資を決定する要因として”そこまで”大きいものではありません。
むしろ彼らは、その投資から実際どれだけの需要(稼働率)が得られるのか?どれだけの利潤が得られるのか?という部分により注目している事がわかりました。
なぜ「利潤率」ではなく「純利益率」なのか?
今回使用する投資関数において、稼働率以外の変数は純利益率になっています。
しかしなぜ純利益率を使用するのでしょうか?
元々の初期カレツキアンモデルでは利潤率が用いられていました。例↓

[γu]と[γr]は反応性パラメーター兼アニマルスピリット。
では、ここでよく考えてみましょう。
稼働率が上昇している時、利潤率は上昇していないとおかしいですよね?なぜなら利潤率は以下のように書き換えることも可能だからです。
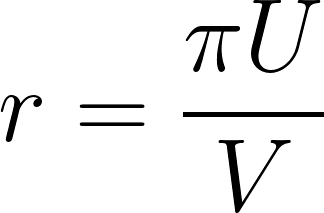
明らかに利潤率は稼働率の関数であり、定数ではありません。
ではもし定数として扱うには、稼働率の上昇と共に純利益率(利潤シェア割合=π)が下がってゆく必要があります。(本来は定数のπが変化すると考える時点でもうおかしい)
利潤率は利潤量と資本ストックの比であり、純利益率というのは利潤量と現状生産高との比を表します。
では純利益率が下がるという事は、経済全体の生産量の内訳に資本家が占める割合が減るという事です。これは言い換えればより多くの労働者への分配を意味します。
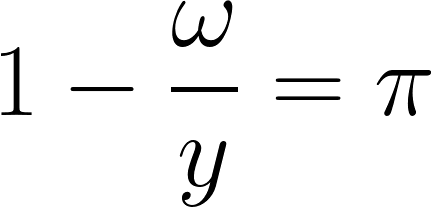
ωは実質賃金率、yは労働生産性
さて実質賃金率と純利益率には上記のようなトレードオフの関係が存在します。
という事は純利益率の低下は労働コストの上昇と同義であり、このようなコストの圧迫が投資の意思決定に景況を与えないと考えるのは些か不自然です。(スラッフィアンは実際の利潤率でなく、通常利潤率にする事で上記の問題の改善を試みた)
よって資本家は利潤率でなく、純利益率をその意思決定に使用すると考える方が理論的にも実証研究的にも”良い”のです。
投資の内生化:稼働率と成長率
言葉の定義
P=価格水準、q=実質生産高、w=一人当たりの名目賃金、L=雇用量、R=名目利潤量、s=資本家の貯蓄性向、ω=実質賃金、y=労働生産性、r=実現利潤率、rn=通常利潤率、re=予想・期待利潤率、π=純利益率、V=資本係数、U=実現稼働率、Un=通常稼働率、Ue=予想・期待稼働率、g=成長率、t=時間、γu=稼働率への反応性、γπ=純利益率への反応性、K=資本ストック、c=動学的調整パラメーター(ただの調整速度パラメーターなので使いまわします。)
前提条件と仮定
1種労働、1財、2階級モデル。労働者は利潤を受け取らず貯蓄もしない。
資本家は貯蓄し利潤を受け取る。閉鎖体系の純粋経済。
ケインジアン安定条件が常に満たされている↓

レオンチェフ型生産関数を採用
導出

上記の国民総所得の定義式より、マクロ均衡条件(I=S)が満たされる時は、以下のような稼働率と成長率の関係性が満たされる。
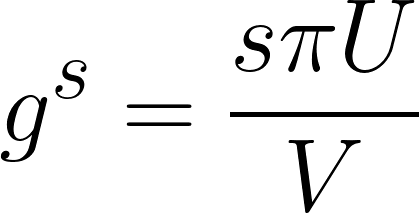
ではThe Bhaduri&Marglin型投資関数より各期の投資は

と定義する。
では経済がケインジアン安定条件を満たす場合、貯蓄式と投資式の関係性は以下のように図示できる。

経済がマクロ均衡条件を満たすのは予想稼働率と均衡稼働率が同値になる点なので……

均衡点までの移行過程は以下のとおりである。
来期の投資は今期の予測稼働率と実現稼働率との差分を考慮して決定されるので……

今期の実現稼働率は、前期の予想稼働率からもたらされたものなので、以下のように書き換えれる。

上記の式を代入し、一般項を求める。

当然これのlim時間を無限大にすれば……

となり、収束します。
PC曲線とED曲線
稼働率と成長率の関係性が分かったところで、利潤率と稼働率の関係性も求めましょう。
PC曲線とは価格・コスト曲線の略称で、サプライサイドから見た稼働率と利潤率の関係性を表します。
ED曲線は有効需要曲線の略称で、需要サイドから見た関係性を表します。
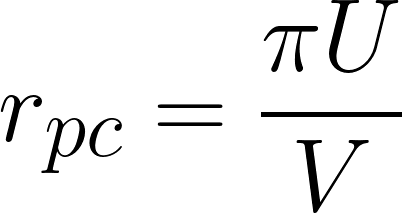
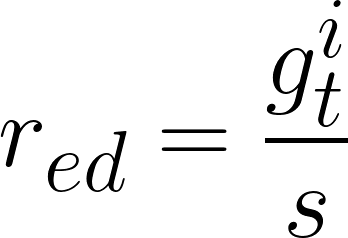
よって、成長率と利潤率は以下のように繋がってます。

賃金主導型成長と利潤主導型成長
カレツキアンモデルの一番の特徴は、なんといっても分配と成長の分析でしょう。
稼働率の均衡式を成長率の定義式に代入すると、純利益率と成長率の関係性がわかります。
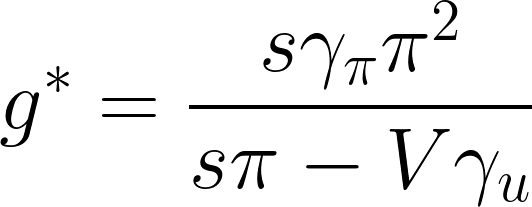
したがって成長率と純利益率の関係性は非線形で、非対称です。

では利潤主導型成長と賃金主導型成長を分け隔てる条件とはいったん何でしょう?
両成長の境目である、一階微分=0地点を実際に計算すると以下のようになります。

この感じ、見た事ありませんか??
そう「ケインジアン安定条件」です。ケインジアン安定条件は

でしたね、これは予想稼働率への反応性が貯蓄のそれを超えてはいけない事を意味します。
もっと簡単に言えば貯蓄式の傾きより、投資式の傾きの方が小さくないといけないという意味です。
では、一階微分の式を書き換えてみましょう。
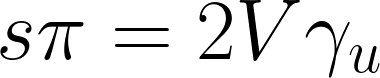
となり、ケインジアン安定条件は守られています。
利潤主導型成長は反応性と資本係数を二倍にしても守られるようなケースで発生します。
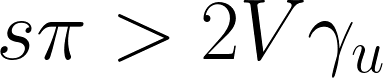
これはケインジアン安定条件が非常に硬く守られている事を意味します。⤵

逆にケインジアン安定条件が緩く守られる場合は賃金主導型のレジームが発生します。
(ケインジアン安定条件自体は守られているが……)

(固く守られているわけではない)
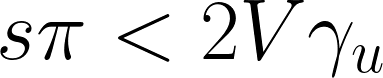
すると賃金主導型経済成長には、貯蓄性向と稼働率の反応性がそれなりに近くなければいけません。しかし近すぎるとケインジアン安定条件を守れず正に発散してしまいます。
つまり必然的に賃金主導型成長は、圧力の高い経済状態である可能性が高いという事です。
賃金・利潤フロンティア、インフレーションバリア
ではここで、経済が100%のキャパシティーに陥った場合どのような事が起きるのか?そして番外編的にインフレーションの数理モデルを紹介します。
賃金・利潤フロンティア、別名インフレーションバリアは、ネオケインジアン、スラッフィアン、マルクス、古典派の経済学派たちに共通する概念(もしくは共存可能)で、利潤と賃金がトレードオフになる世界(=サプライサイドが支配的な経済)です。
導出自体はカレツキアン的な国民総所得の定義式から簡単にできます。
仮定:経済が通常稼働率上に存在する

まず両辺を産出高で割ります。そして上記の仮定と、国民総所得の定義と、マークアップ率の定義より、現状の名目利潤量(R)は資本と価格水準、標準利潤率の積と同値になるので……
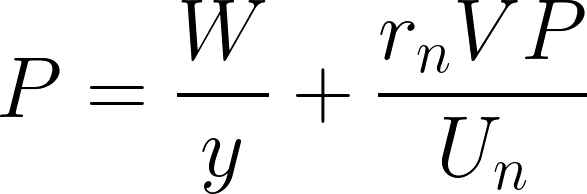
となり、これを実質賃金率で解けば……
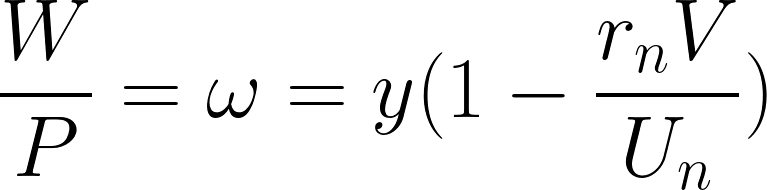
と書き直せます。
では最初につけた仮定を外し、稼働率100%時の場合を考えます
フロンティアの面積が最大になるのは稼働率が最大の地点(U=1)ですので、式を書き直します。
利潤率は稼働率の関数ですので、100%稼働時の利潤率をrfcと表します。
よって下記のように表せます。
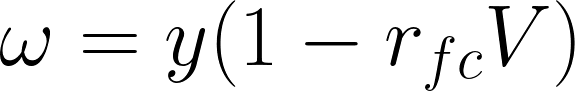
グラフ上に図示すれば……
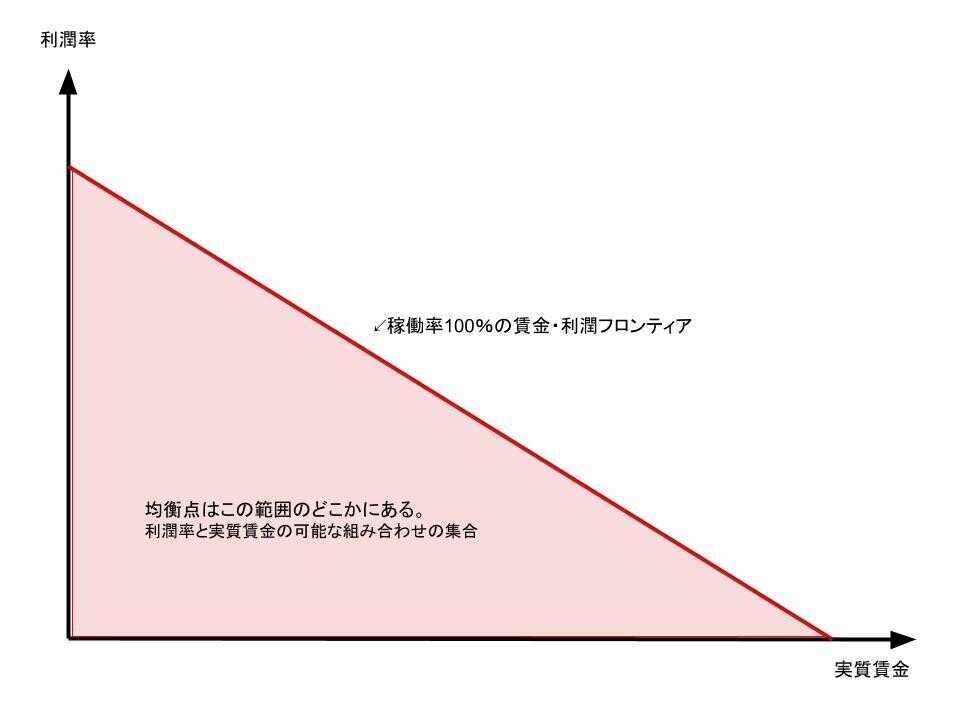
これは経済がどこまで需要主導で動けるかを表します。
稼働率100%の地点に達しない限り、経済の主導権はすべて需要側にあります。
しかしひとたび完全雇用で完全操業に至ってしまうと、経済はサプライサイドに制約されることになります。
マルクス、スラッファ、古典派はどのように考えたのか?
先に書いた通り、このインフレーションバリア(賃金利潤フロンティア)はマルクス、スラッファ、古典派といったサプライサイドの経済学で共通してみられる概念です。
彼らはこのフロンティアが常に右下がりで、常時経済がフロンティア上で操業すると考えました。
古典派のケースは一番わかりやすいでしょう、経済が文字通り上記の図の稼働率100%の直線上にいるパターンです。
ただマルクス派やスラッフィアンは、不完全な操業でも”もし常にサプライサイド側の設定して通常稼働率に経済が収束するなら、トレードオフは成立する”と考えました。
加えて、スラッフィアンは「もしフロンティア上に”右上がり”の区間があるなら、それは非連続になる」と予想しました。
ではカレツキアンは?
カレツキアン、もといポストケインジアンは「この賃金利潤フロンティアは常に右下がりではないし、経済が常にフロンティア上にあるわけでもない、加えて両者の関係にトレードオフが必ずしも成立するわけではない」と考えました。
カレツキアンの賃金・利潤フロンティア
まずマクロ均衡条件を満たす、純利益率と成長率の組み合わせの式に貯蓄性向の逆数をかければ、純利益率と利潤率の組み合わせに変わります。
それに加えて、純利益率と実質賃金率には下記のようなトレードオフの関係が存在するので……
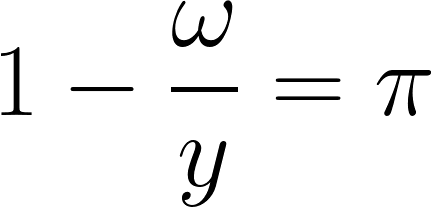
したがって、実質賃金と利潤率のマクロ均衡条件を満たす関係式は……

となり、これを先ほどのフロンティア上に表示しましょう。

カレツキアンの世界では、経済はこの橙色の曲線上に存在します。
先にみたように、閾値を超えればコストの上昇(=実質賃金の増加)が有効需要を増やし、成長率を増大(=利潤率も増加)させます。
つまりフロンティア内部に関係性が右上がりになる区間は存在するし、経済が常にフロンティア上に存在するわけでもありません。(稼働率が100%になるまでは)
またスラッフィアンが予想した通り、右上がりの関係性を示す曲線は需要サイドから導出され、右下がりの関係だけを示す直線は供給サイドから導出されており、お互いに関係はなく、非連続です。
番外編:階級闘争型インフレーション
ポストケインジアンにおいてインフレーションは、フィリップスカーブでもNAIRUで決定されるわけでもありません。
MMTの教科書であるMacroeconomicsでは「インフレーションは階級闘争からくる」として扱っています。
では、このような賃金インフレーションをどのようにモデル化できるでしょう?
今回はそんな疑問に答える階級闘争型インフレーションモデルを紹介します
前提と世界観
t=時間、πn=目標純利益率、ωf=資本家の望む実質賃金率、ωw=労働者の望む実質賃金率、Ψ=資本家の闘争力パラメーター、Ω=労働者の闘争力パラメーター
労働者は賃金を決定する権利を持ち、資本家は価格を決定する権利を持つ。
労働者は、自らの望む実質賃金になるよう賃金を上昇させる。
資本家は、自らの望む純利益率になるよう価格を上げる。
導出
純利益率と実質賃金のトレードオフの関係より、資本家の目標とする純利益率は実質賃金率として表せる。
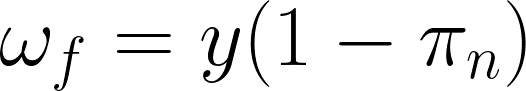
資本家は、現状の実質賃金(W/P)が自らの望む値になるよう、価格を上昇させる。
よって価格の上昇率は、この場合……

労働者は自らの望む実質賃金に賃金を上昇させるため…

上記の通りになる、図示してみよう。

青色が賃金の変化量を表し、赤色が価格の変化量を表す。
では、変化率が互いに等しくなる実質賃金は……

となります。
ふう~疲れた。
ちなみに、この階級闘争型インフレーションとインフレーションバリアはつながります。
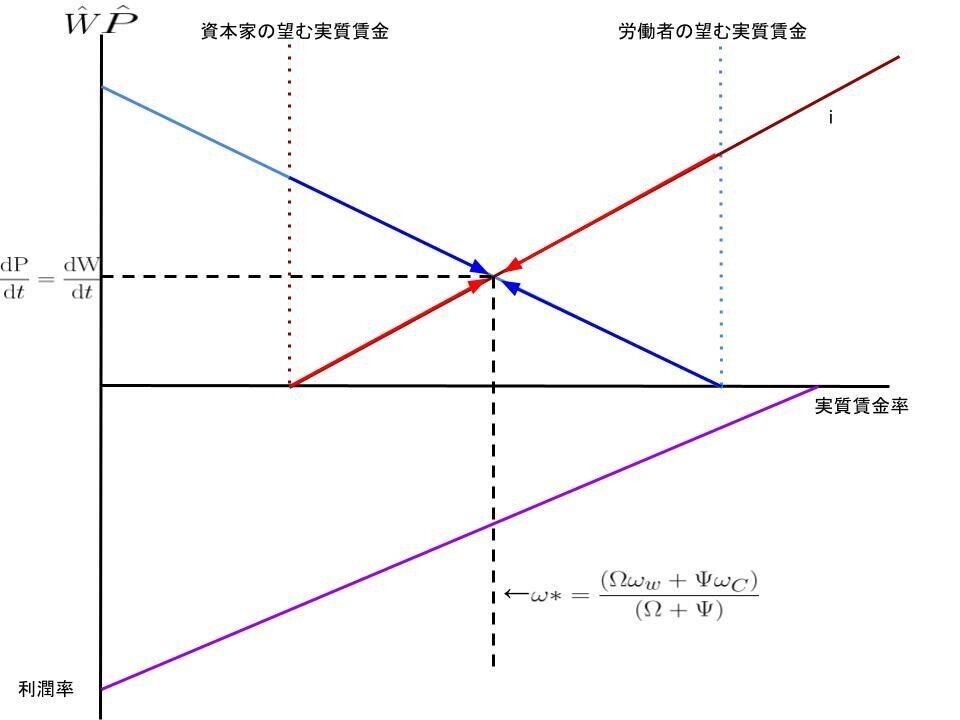
ここではあまり深堀しないけど★
とーことで番外編終了
カレツキアンモデルに対する批判とその対応
カレツキアンモデルには幾つかの批判が存在します。ここでは一番代表的な批判を紹介しておきましょう。
最も代表的なのは「通常稼働率、すなわち企業が望む利潤率が達成される稼働率と、現実の稼働率・利潤率が等しくなるとは限らない」という問題です。
通常稼働率が実際の稼働率と等しくならない事は何が問題なのか?
古典派やマルクス、スラッフィアンから言わせてみれば、通常稼働率とはその名の通り「通常」の稼働率であり、それは長期的な”予測・期待稼働率”と等しくならないとおかしい。と考えています。
また先に書いた通り、彼らはもし通常稼働率に長期的に経済が収束するなら、それは経済が常にインフレーションバリア上に存在する事を意味し、需要サイドの力は所詮短期的な影響しか与えず、サプライサイドの経済学が長期的に支配する。とも考えている訳です。
端的に彼らの主張を要約するなら「”通常稼働率=期待稼働率=均衡稼働率”となっていない限り、調整は終わっていない。もし本当に調整されたならカレツキアン的な結論は消えて、サプライサイドが支配的になる」という事ですね。
カレツキアンからの反論と対応
当然、言われたまま黙っているわけではありません。
上記の批判に、カレツキアンは大体3通りで答えています。
一つ目の回答:「期待自体は完成しており、通常稼働率が期待稼働率と等しくならないのは、新たなマクロレベルのパラドックスであると考えるべきだ」
簡単に説明すると、予想・期待稼働率は均衡稼働率と収束値で等しくなっている。↓
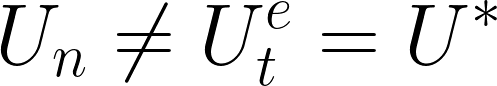
企業・資本家の自らが期待した利潤率は、実際に叶っており期待は完成されている。と解釈し、加えて各企業は操業する上で通常稼働率も考慮に入れながら投資を決定し調整しようと試みるが、マクロ集計的にその調整に失敗してしまう。そういうパラドックスとして理解されるべきだ。って感じです
以上の主張は、以下のような投資関数で特に説得力が出るでしょう。

上記のような投資関数では、通常稼働率が投資決定に影響を与えています。
今回は使用しなかったけどね(条件が厳しくなっちゃうのと、無駄に複雑になるから)
二つ目の回答:通常稼働率には許容範囲がある
企業の通常稼働率には許容できる範囲、つまり”通常”とみなせる範囲があり、その範囲に均衡点がある限り期待は完成しており、調整は終わっている。
なので無理に経済を外生的な稼働率に収束させようとパラメーターを調整する事は、恣意的で意味のない行為だ。という反論です。
三つ目の回答:仮に調整が行われたとしても、カレツキアン的特徴は失われることはない。そして需要サイドが経済の主導権を握る事も変わらない。
さて、三つ目の回答は若干複雑です。
ここでは、できるだけ簡素化した形で三つ目の回答を正当化したいと思います。
批判に応えるカレツキアン:通常稼働率の内生化
マルクス、スラッフィアン、古典派からの批判に積極的に答えるためには、彼らの言う通りになったとしても、カレツキアン的特徴が保持される事を証明すれば良いのです。
やり方はたくさんあって、貯蓄性向が内生化されるパターン、投資式のパラメーターが調整されるパターン、価格が固定の通常稼働率に収束するよう調整されるパターン等々、沢山です。
この記事では通常稼働率自体が内生化される手法を取ります。ちなみに、この手法は教科書(PK Economics :new foundations)に載ってなかったので、正直理論的にあってるかは不明です(笑)
教科書内では、二つの微分方程式を用いて安定性を分析したりラジバンダリで僕には全然理解できなかったので、できるだけ簡単にしました。
僕の調整過程は価格の調整(=純利益率)を通して経済を均衡に持ってゆくパターンで、類似の手法はジョアン・ロビンソン等が使用しました。
しかし、ロビンソン的調整パターンは”古典派達の批判”を肯定するような結論を導き出してしまいます。
では僕の調整パターンと、ロビンソン的調整パターンを比較してみます。
ロビンソン的調整パターン

さてロビンソン的な調整パターンは、外生的な一定の通常稼働率に経済が必ず収束するように通常利潤率が変化し、純利益率が調整されます。
純利益率の定義式を見るとよりわかりやすいかもしれません。↓
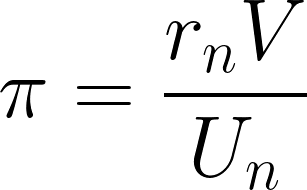
僕(笑)の調整パターン

さて、僕の調整過程はロビンソンとは逆のパターンです。
常に固定の通常利潤率に経済が収束するように、通常稼働率自体が変化し(=純利益率の変化)価格が調整されます。
僕のやり方は微分方程式がたくさん出てきたりしないし、高校生レベルの数学が分かればだれにでも理解できるので、皆に馴染みやすいと思います。
解を求めるだけなら中学レベルの数学しか使用しないし、簡単でしょ?
ただ、だからといって調整方法が単純とは限りません。
この調整方法は、標準稼働率の修正を行う一つの微分方程式を通して企業の価格、純利益率が調整されます。
つまり一つの調整式で、内生化される変数の数は実質的に通常稼働率と純利益率と価格の三つになります。
均衡・収束値の導出
では実際に通常稼働率を内生化しましょう。
通常稼働率自体が均衡稼働率に引き寄せられるように調整されるので……
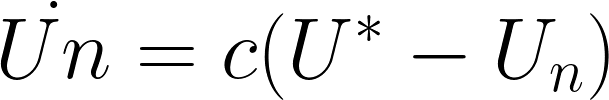
となり、均衡稼働率は……

なので、上記の式を調整式に代入します。

変化量がゼロになる地点が収束点なので、ゼロを代入し式を簡単にします。

では両辺に通常稼働率を掛ければ、通常稼働率に対する二次方程式になるので、解の公式で収束点を求める。

これにて収束値が導出できたので、分析していきましょう。
解の存在条件
通常稼働率の解は判別式を使用して求められます。
解が一つ
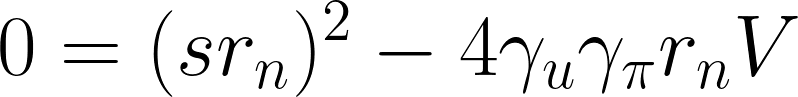
解が一つの場合、成長率はdg*/dπ=0の地点になる。
解が二つ

解が二つある場合は、低い方は利潤成長型の経済に収束する事を意味し、高い方が賃金主導経済を意味する。
解なし

正に発散します。しかしながら通常稼働率は、0以上1以下の値しか取りません。したがって発散する前に経済がインフレーションバリアに衝突し、そこで安定?する。(おそらく非常に大きなインフレーションを伴う)
位相図と経路、動学的安定性の問題
今回は解が二つのパターンだけを詳しく見ていきましょう。
解が二つあるとき、以下のように位相図を描けます。

安定的な調整過程
経済のマクロ均衡条件が満たされ、稼働率の変化量が零になる点に収束した後、資本家は自らの設定した通常稼働率と均衡稼働率を比較し、マージン率の変化を通して調整が行われます。
もし現状の稼働率が通常稼働率よりも低い場合、企業は通常稼働率を引き上げます。これで企業はより低い通常稼働率でも彼らの望む目標利潤率を達成できるようにマージン率を引き上げます。=価格の上昇
そして価格の上昇は労働者の実質賃金を低下させ、結果的にマクロ全体の有効需要を減らしてしまうので、均衡稼働率・成長率・利潤率が共に悪化します。
しかし一連の調整と景気後退サイクルが進行するにつれて、価格の上昇からくる利潤収入が、有効需要低下の負の影響をかき消し、利潤率を引き上げ始めます。
最終的に利潤率が、企業の目標利潤率まで引きあがり、調整は終了します。
この様な調整過程で生まれる収束点は必ず利潤主導型経済に対応するモノとなります。
さらに残念な事?に利潤主導型は低圧力経済故にインフレの可能性が低く、安定性が非常に高いです。
不安定な調整過程
不安定な均衡点は賃金主導型経済の領域に必ず存在するため、利潤主導型経済では悪影響になる価格の低下が、経済をより加速させ発散してゆく。
しかし、これは若干モデルをまんま解釈しているだけで現実的な物とは言えない。
というのは、先にも書いた通り”通常”とみなせる稼働率には範囲があり、それは100%を超えることはないからです。付け加えて均衡稼働率が100%近傍に差し掛かれば、むしろコストの上昇圧力がかかり始めるでしょう。それに応じで価格を引き上げる可能性もあります(それは通常利潤率かもしれない)
また忘れてはいけないのがインフレーションバリアの存在です。100%以上の稼働率を長期的にしようと思えばサプライサイドの制約にかかる事になるでしょう。
すると経済が無限に発散してゆく事はあり得ないし、現実的には100%近傍で安定するでしょう。
得られる結論
さてマルクス、スラッファ、古典派から出た批判に応えた上記のモデルから、カレツキアン的世界観が垣間見えます。
まず重要な結論として「長期的に経済が通常稼働率に調整されたとしても、ケインズ的特徴は失われないし、カレツキアン的特徴が失われることもない」という事が証明できました。
次に「経済には安定的な均衡点が存在し、それは高い確率で利潤主導型。賃金主導型は不安定であるが存在する。」という事が示されました。
インフレーションバリアの拡張と実物制約
さあカレツキアン的なインフレーションバリアはもうご存じですね!
先に得られた結論より、最終調整された経済はの稼働率は……
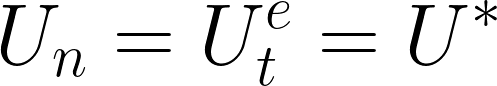
であり、利潤率は………
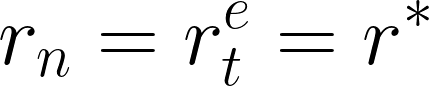
ではこれをインフレーションバリアに組み込むと面白い動きが見れます。

解が二つ存在し、片方は利潤主導型、もう片方は賃金主導型。私たちが見てきたとおりですね。
そして、各交点で均衡条件たる
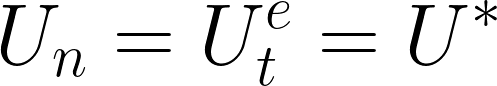
はしっかりと守られている。
思考実験的に均衡利潤率がめちゃくちゃ高い場合はどうでしょう?

利潤主導型はフロンティア内部に存在しています。
しかしながら賃金主導型”だった”方は100%の壁に衝突し、利潤主導型のエリアまでひっぱられています。
これは「経済が実物的な制約に当たってしまった」事を意味します。
よくMMTerが言う言葉ですね。
まとめ:比較動学
最後は今回の記事で紹介してきたモデル達をひとまとめにして、ポストケインジアンの動学モデルが、どのように繋がっているかを紹介して終わろうと思います。(番外編は含まない)
ではどうぞ!!
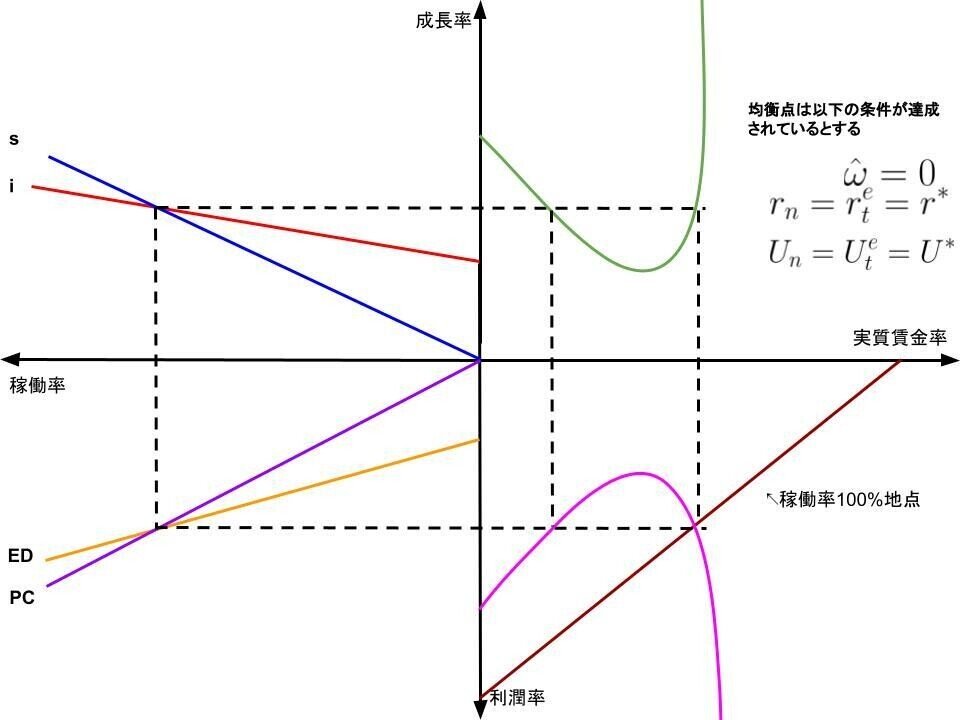
はい、うつくしい~~
もう疲れたわ、なんか語彙力失ってる。
まあ、書いておかないといけない事は全部入れてあるから大丈夫でしょう。
これにて、実物的カレツキアンモデルの紹介を終わりたいと思います。
一人でも多くの異端派経済学に興味ある人の目に留まることを願っています。
次回はこの記事が理解できている事を前提に、カレツキアンモデルをSFCモデルと限定的に拡張させ、金融側面を取り込んだモデルを紹介しようと思います。
ミンスキーの理論をカレツキアン的なモデルで理論化します。うぇい!
はい、おやすみ~
