対称性を利用した定積分(数3・積分)
今回の問題(質問)
対称性を利用した定積分です。
積分は難しいですね。見慣れない関数だと特に大変です。出来るようなるコツは
とにかく様々な積分方法を経験しておくこと
ではないかと思います。数学ですが、少し暗記科目のような要素があります。
では今回の問題です。
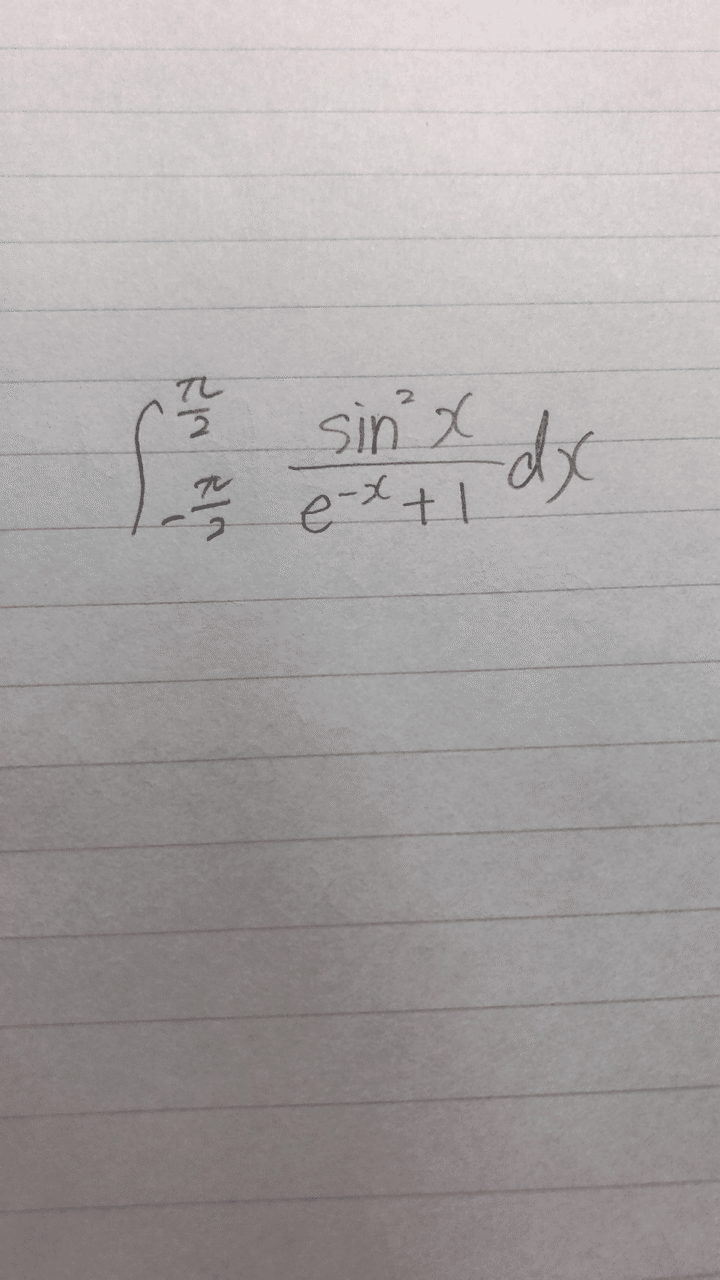
です。置換積分やら部分積分などなどを駆使してもなかなか出来ない定積分ですね。
ただ、分子が偶関数で分母がe^-x+1(eのマイナスx乗たす1)という特徴的な形です。この形は
「対称性を利用した定積分」
として有名な形なのです。この特徴をよーく覚えておきましょう。以下にこの「対称性を利用した定積分」の典型的なやり方を示しておきます。
対称性を利用した定積分のやり方
少し読み難いかもしれませんが、画像で貼っておきます。基本はこの形ですので、これを理解して覚えておくといいでしょう。

問題の解答
上の定積分のやり方を理解すれば、同じように解けばいいだけなので、以下のように今回の問題は解けます。

この他にも対称性を利用した定積分の典型例はあります。追い追い紹介していければなと思います。
それでは最後まで読んでいただいてありがとうございます&お疲れ様です。
#数学3
#高校数学
#定積分
