周波律 〜ピタゴラスコンマを越えるための調律法〜 （1）

（この記事では、新しい調律法を紹介しています。これまでの調律をより高い精度に引き上げる可能性を持った調律法ですが、まだ発見されたばかりのため、理論・実践面における多くの検証が必要です。お気づきのことがございましたら、些細なことで構いません。コメント欄か、クリエイターへのお問合せより、お願い致します。）

ここでは、その新しい音律を‘周波律（しゅうはりつ）’と呼ぶことにします。周波律とは、ある音の振動数を等分することで、音階を組み立てるという考え方です。振動数の単位にはヘルツ（hz）を用います。ヘルツとは、一秒間に何回、音が振動するかを定義した単位です。一秒間に一回の振動なら、1hzです。

それでは、具体的な調律の方法に入ります。
まず、基音としたい音をヘルツで選択し、それを12で割ります。今回は整数で割り切れる数を探し、432hz（＝A）の音を基音とすることにしました。

まず、432を12で割ります。36という値が出ました。432hzに36hzずつ足していくと、12回目で、1オクターブ上の864hzにたどり着きます。
五線譜に直して、振動数比を上に書き添えたのが、図1です。

［図1］周波律音階

こうして見ると完全一度（1:1）、長三度（4:5）、完全四度（3:4）、完全五度（3:2）、長六度（3:5）、完全八度（1:2）の音が12音の中に含まれることが分かります。これを「周波律音階」と呼ぶことにします。

もちろん、このままでは十二半音階の音になりませんし、全音階（ドレミファソラシド）も導き出せません。周波律音階から全音階を得る方法を考えます。上の表において、ラから始まる基音をドに読み替え、英音名式に改めたのが、図2です。

［図2］’ド’を基音にした周波律音階（英音名式）

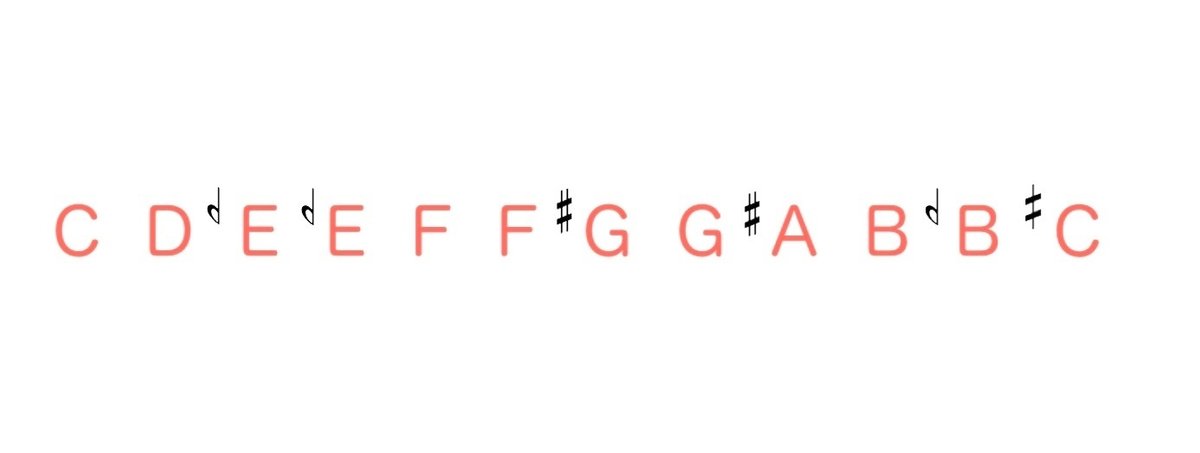
全音階上の長ニ度・長七度にあたる音（レとシ）が、周波律音階には含まれないことが分かります。そこで、周波律の複合形を用います。この音階の完全五度上の音階に注目してください。ソの音を基音にした周波律の音階です。［図3］に緑色で示します。

［図3］’ソ’を基音にした周波律音階（緑）

ソの周波律音階は、完全五度上にレの音、長三度上にシの音を含みます。この固有音を、ドの周波律音階に取り入れます。［図4］

［図4］二つの周波律音階から導き出された全音階

これで全音階の音が揃いました。同様に完全五度上の音階を借りながら、十二半音階に近い値をとります。［図5］

［図5］二つの周波律音階による十二半音階

これまでの一連の音を聴かれたい方は、以下の動画をご参照下さい。

それでは、この調律法から導き出される音階が、これまでの調律とどう違うか、どのように役立つかを、次回の記事から書き進めたいと思います。