
物理 原子分野の攻略1 光電効果
今回は、高校ではあまり詳しくやらない原子分野の攻略法について解説していきます。
光電効果
▼光電効果とは?
光電効果とは、ズバリ
物質に光を照射したときに、金属から電子が放出される現象
です。

この当てた光は、実は矢のようにまっすぐな物では無く、実はうねうねとした波の状態で当たってきます。光は実は波なんです。
なので、当然振動数や波長などが存在する訳です。
振動数とは1秒間に繰り返された単振動の数です。簡単に言うと、うねうねの数です笑
この振動数を普通はν(ニュー)という文字で表します。V(ブイ)ではありません。
実は、振動数がある一定の数値よりも多くないと、光電効果はおきません。
そのある一定の数値(光電効果が起こる最低ライン)をν0と普通は表します。
○ ν>ν0
また、この当てた光は金属から電子を放出させるくらいですから、ある程度のエネルギーを持っています。このエネルギーは、実は次の式のように表されることが分かっています。
○ E(光が持つエネルギー)=hν
このhはプランク定数という、ただの数字です。特別な意味はありません。ちなみに、数値は
6.63×10^-23です。^は〜乗を表します。
では、光を当てたらどのような現象が起きているのか、詳しく見ていきましょう。先程と同じ写真をもう一度載せます。

実は光を当てたらそのまま同じエネルギーが放出されるわけではありません。電子を放出するために必要な最小のエネルギーがあります。これを仕事関数と言います。
○ 電子を放出するために必要な最小のエネルギーが仕事関数W
この仕事関数は普通Wとします。
この仕事関数というエネルギーが働くからこそ、電子が放出されるのです。
そして、金属から出ていった電子は当然ながら、ある程度の速度で出ていきます。なので、運動エネルギーを持ちます。私たちが普段目にする物体が動いているときの運動エネルギーと一緒です!
この電子の出ていく速さはVmaxと表します。なぜmaxなのかというと、あらゆる光の粒子が金属に当たり、それに伴いあらゆる光電子が外に出ていきますが、その中で最も速い光電子の運動エネルギーを計算するからです。
また、光が当たる前後でエネルギーは保存されており、次のような現象が成り立ちます。
光が持つエネルギー
=仕事関数+放出された電子の運動エネルギー
電子の質量をmとすると、以下の式のように表せます。
hν=W+1/2mVmax^2
この式は覚えなくて良いです。「ポイント」のところと、光が当たる前後でエネルギーが保存されることだけ覚えてください。
※電子が金属から飛び出すための条件について
ちなみに上の式を変形すると
hνーW=1/2mVmax^2となります。ここから電子が飛び出すための条件が分かります。電子が飛び出しているということはVmax>0です。そのため、
hνーW(=1/2mVmax^2)>0となり、hν>W
よって、ν>W/h
これは電子が飛び出すための条件となり、このW/hはν0と同じものになります。
この式自体は覚えなくて良いですが、流れは覚えておいて損はないです!
▼光電管について
そもそも、電子が飛び出る時の速さはどのように測れるのでしょうか?
それは光電管というものを使用すると測れます!

これが光電管です。図式化すると以下のようになります。

○ 光電管の仕組みを理解しよう
光電管の仕組みについて説明します。
光電管には、小さい電極aとお椀型の電極bがあり、2つの電極はそれぞれ直流電源に接続します。アースした電極b側を0[V]とし、電極aの電位は、プラスからマイナスまで自由に変えることができるものと普通はします。
この光電管では、電極bに向かって光を当てます。そして、先ほど学習した光電効果により、電極bからは電子が放出されます。この電子が電極aに向かって移動していき、さらに導線を伝って電極bに再び戻ってきます。このとき、流れる電流は、光を当てたことにより流れる電流なので光電流といいます。
〔流れ〕
この光電管の電極bに向かって、光を照射。
↓
光電効果により、電極bからは電子が放出される。そして、電子は電極aへと移動する。
↓
電子は導線を通って電極bの方へと戻ってくる。このとき流れる電流を光電流という
そして、ここで大事なのが、電極a(小さい方の電極)の電流と電圧の関係です。もう一度光電管の図を見てみましょう。
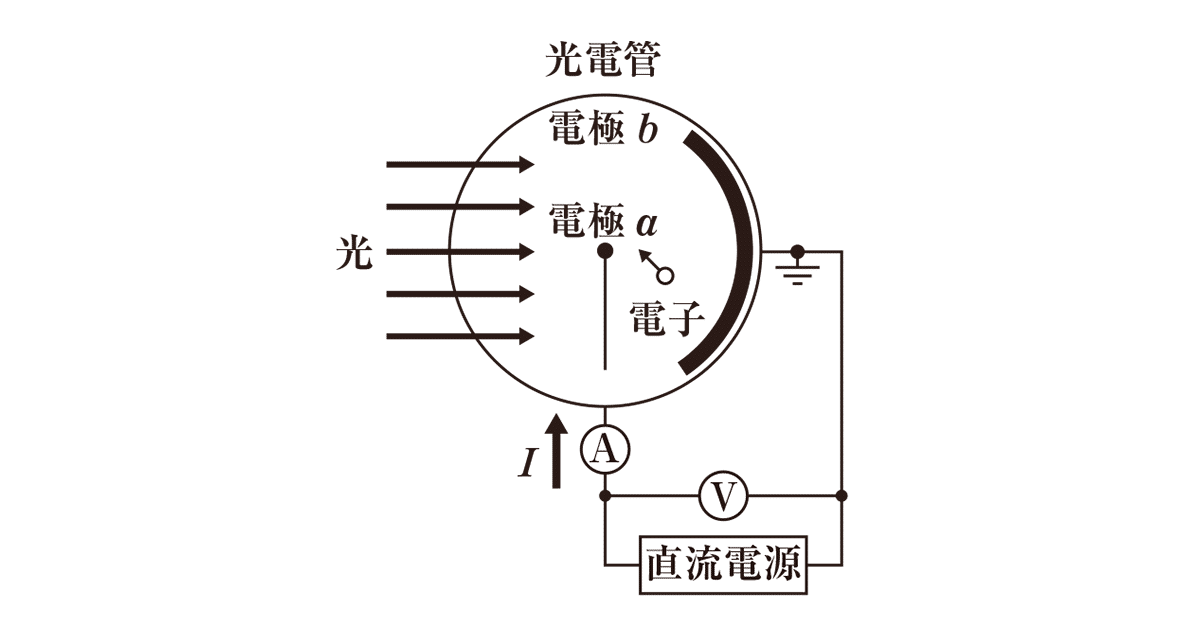
上図では直流電源から電極aへと電流が流れ、電極aから電極bへと電流が移動しています。ここで電圧を0にして直流電源からの電流を止めてみたらどうなるでしょうか?実はこの状態でも電流は流れています。なぜでしょうか?
それは光電効果のおかげです。電極bに対し光を当てることで電極bから電極aへと電子が放出されています。つまり、電極aから電極bへと電流が流れていることになります。(電流の向きは、電子の流れの向きと逆でしたね?)
もちろん電圧をかけた方が電流は大きくなります。しかし、実はある一定の電圧をかけると電流の大きさは変わらなくなります。この変わらなくなったときの電流をIoと普通はします。10(じゅう)ではありません。Io(アイゼロ)です。
○ 電極aの電圧が無限になるとき、電流の大きさはIoで一定
では、逆に直流電源からの電圧をマイナスにかけて、電流を逆にする(電極a→bからb→aにする)とどうなるでしょうか?
答えは、「光電効果によって元々a→b方向にかかっていた電流と相殺されて、最終的に0Aになる」です。光電効果によって電流が元々a→b方向にかかっており、それと逆方向のb→a方向に直流電源から電流を流しているのです。徐々にa→bの勢力が弱まり、最終的に0になるのは、なんとなく想像つきますよね?
この電流が0Aになった時の電極aの電圧は、普通-Voとします。この-Voというのは、電極bを0Vとしたときの値です。また、0Aになったときの-Voの電圧を阻止電圧といいます。
○ 電流が0Aになった時の電極aの電圧は-Vo
これらの現象をグラフに表したのが以下のものです。

これは非常に有名で頻出なので、覚えておきましょう
▼光電管の力学的エネルギーについて
以下のような内容を、光電効果のところで述べました。

実はこの実験でも、流れる電子の中で速いものと遅いものが存在します。なので、電流が小さくなるに従って、遅い電子から順に流れなくなっていきます。逆に速い電子はまだ流れています。これは自然淘汰のようなもので、弱いものから順に消えていくと言うことと少し似ています。
そして、最も速い電子でも、電極bを0Vとしたときの電極aの電圧が-Voのときに初めてそのスピードが失われます。つまり、電極aが-Voのときに全ての電子が運動エネルギーを持たなくなるのです。このとき、a→bの方向に流れていた電流がなくなります。そのためb→aに流れていた電子の流れもなくなります。もう一度、光電管を見てみましょう

b→aの電子の流れでは、力学で習った「力学的エネルギー保存則」が適用されます。なので、電極aと電極bで力学的エネルギーは保存されています。
○ 電極aと電極bで力学的エネルギーは保存されている
電極bの電圧を0としたとき、電極aの電圧が-Voであり、このとき最もスピードの速い電子でもギリギリ届かないです。このスピードをVmaxと普通します。なので、電極aに辿り着く直前の電子の運動エネルギーは1/2mVmax^2となります。
○電極aに辿り着く直前の電子の運動エネルギーは1/2mVmax^2
さらに、電子にも位置エネルギーが存在し、計算方法はe×(電圧)です。なので、電極aに辿り着く直前の電子の位置エネルギーはe×(-Vo)です
○電極aに辿り着く直前の電子の位置エネルギーはe×(-Vo)
よって、電極aの力学的エネルギーは1/2mVmax^2+e×(-Vo)となります。
一方で、電極bでは、電子はaに向けて出発しようとしているところなので、まだ動いていません。よって、スピードはありません。そのため、運動エネルギーは0です。また、電極bは0Vとしているので、位置エネルギーもe×0で0となります。よって、力学的エネルギーは0です。
今の話しを、以下の図としてまとめました。

電極aの1/2mVmax^2+e×(-Vo)と、電極bの0が一致するので、式としては以下のようになります。
1/2mVmax^2+e×(-Vo)=0
ゆえに、1/2mVmax^2=eVoです。
この式が成り立つので、飛び出す電子のスピードが分かるのです
ここでもう一度グラフを見てみましょう

電流がloで一定になっている部分があります。電流とは、1秒間に流れる電気の量のことです。この間のことについて考えると、1秒間に飛び出る光電子の数をnとすると、次の関係が成り立ちます。
○lo=en
最後に
物理を初歩から学習したい場合、こちらの物理のエッセンスを購入しても良いでしょう。ただ、原子分野に関しては私の今回の説明の方が詳しいと自負しております笑
