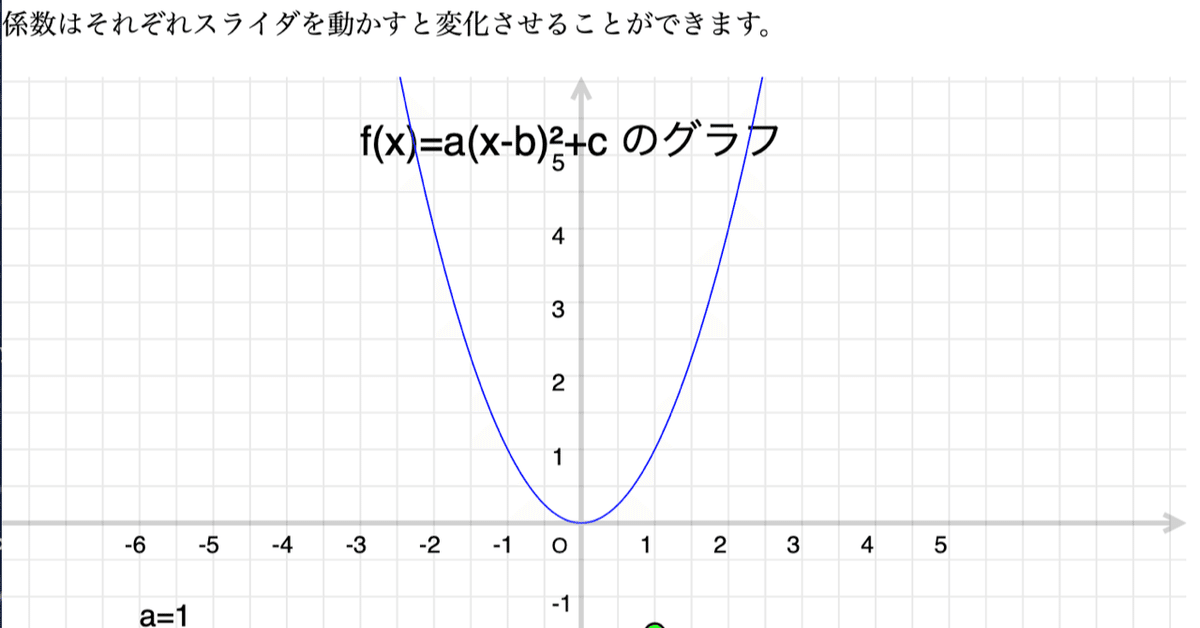
Cinderellaで高校数学：2次関数のグラフ・ベクトル

Pythonで高校数学：2次関数のグラフ(1) 〜(3) ，ベクトルの終点の存在範囲の図を描いたのだけど・・・

2次関数のグラフ(1) の，基本形で係数a,p,q を変化させるものは，matplotlib でスライダを作って，画面設定して，グラフを描く。40行くらい。
たいしたことない？

Cinderela + CindyScriptなら19行で書けて（スライダは作図機能で作る手間がほんのちょっとあるけど） Javascript　にも書き出せるから（CindyJS）そのまま webでできるんだよな。

parabola1.cdy

ソースコードはこれだけ。半分以上占めてるのは軸の目盛りの表示。

drawtext([-3, 5],"f(x)=a(x-b)²+c のグラフ", size->24);
a = |A, G|-5;
b = |C, H|-5;
c = |E, K|-5;
drawtext([-6,-1.4], "a="+a, size->18);
drawtext([-6,-2.4], "b="+b, size->18);
drawtext([-6,-3.4], "c="+c, size->18);
plot(a*(x-b)^2+c);
repeat(12, x, start->-6,
 if(x != 0,
   drawtext([x-0.2, -0.4], x, size->14)
 );
);
repeat(12, y, start->-6,
 if(y != 0,
   drawtext([-0.4, y-0.2], y, size->14)
 );
);
drawtext([-0.4,-0.4], "O");

さらに，ベクトルの終点の存在範囲の図，Pythonだと130行くらい。
これが，Cinderella だと，矢線は幾何の作図機能で描けばいいので，初期設定と関数定義を Initilization スロットに書いて

G.x=0.5;
flag = false;
locus():=(
 if(flag,
   draw(join(B.xy,C.xy),dashtype->1,color->[1,0,0])
 );
);

本体は

wa = 1;
s = G.x/2;
drawtext([-4,7],"$\vec{p}=s\vec{a}+t\vec{b}$ (s+t="+text(wa)+") の終点の存在領域",size->18);
H.xy = s*B.xy;;
K.xy = (wa-s)*C.xy;
D.xy = H.xy+K.xy;
drawtext(B.xy+[-0.5,-1],"$\vec{a}$",size->18);
drawtext(C.xy+[-1,-1],"$\vec{b}$",size->18);
drawtext(D.xy+[0.2,0.2],"$\vec{p}$",size->18);
connect([s*B.xy,D.xy,(1-s)*C.xy],dashtype->1);
locus();

たったこれだけ。

制作にかかった時間も，コードを比べてみれば推して知るべしだ。
なんか，勉強とはいえ，Pythonで教材作るの，ばからしくなってくる。
情報の授業でプログラミングをちょろっと生徒に教えればそれでいいじゃん。

高校教員のためのマニュアルと入門書はだいたい書けた。あとは，ほとんど趣味の領域に入りつつある。